-
Notifications
You must be signed in to change notification settings - Fork 242
Crawler Log Folder
- 🔗 Leetcode Link: Crawler Log Folder
- 💡 Problem Difficulty: Easy
- ⏰ Time to complete: 15 mins
- 🛠️ Topics: Recursion
- 🗒️ Similar Questions: Valid Palindrome, Shortest Distance to a Character, Check Distances Between Same Letters
Understand what the interviewer is asking for by using test cases and questions about the problem.
- Established a set (2-3) of test cases to verify their own solution later.
- Established a set (1-2) of edge cases to verify their solution handles complexities.
- Have fully understood the problem and have no clarifying questions.
- Have you verified any Time/Space Constraints for this problem?
Be sure that you clarify the input and output parameters of the problem:
- How should I handle an empty log file?
- All log files will have at least one input
- What are the time and space constraints?
- Time should be
O(N)and space should beO(1)including the recursive stack,Nbeing the length of the logs
- Time should be
Run through a set of example cases:
HAPPY CASE
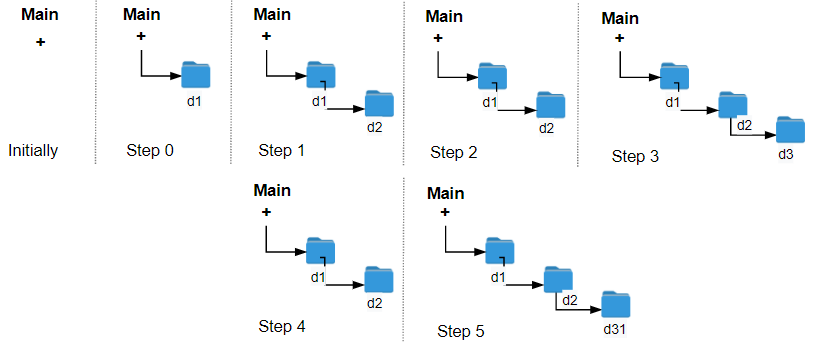
Input: logs = ["d1/","d2/","../","d21/","./"]
Output: 2
Explanation: Use this change folder operation "../" 2 times and go back to the main folder.Input: logs = ["d1/","d2/","./","d3/","../","d31/"]
Output: 3EDGE CASE
Input: logs = ["../"]
Output: 0Match what this problem looks like to known categories of problems, e.g. Linked List or Dynamic Programming, and strategies or patterns in those categories.
- Sort
- Not helpful, we need to maintain the relative order of the logs
- Two pointer solutions (left and right pointer variables)
- Not helpful, we need to move in one direction
- Storing the elements of the array in a HashMap or a Set
- Not helpful, how does the hashmap help us find the distance between characters
- Traversing the array with a sliding window
- Not helpful, we are not looking for a window size
- Stack
- When dealing with file system traversal, stack is a good choice
Plan the solution with appropriate visualizations and pseudocode.
General Idea: We will recursively find the depth of the file traversal logs and that will be the minimum operations to return to root.
1. Write a recursive function to drill into the file system.
a. Set the basecase: Out of bound.
b. Update depth base on log function string
c. Call recursive function on next log item
2. Call the recursive function
3. Return the result.General Idea: We will iteratively find the depth of the file traversal logs and that will be the minimum operations to return to root.
1. Create a stack
2. Add/Remove items from stack
3. Return the size of stack.- Using iterative approach will work here, however the interviewer wants the recursive solution.
Implement the code to solve the algorithm.
Recursive
class Solution:
def minOperations(self, logs: List[str]) -> int:
depth = 0
# Write a recursive function to drill into the file system
def helper(i):
# Set the basecase: Out of bound
if i > len(logs) - 1:
return
# Update depth base on log function string
nonlocal depth
if logs[i] == "../":
if depth > 0:
depth -= 1
elif logs[i] == "./":
pass
else:
depth += 1
# Call recursive function on next log item
helper(i + 1)
# Call the recursive function
helper(0)
# Return the result
return depthclass Solution {
int depth = 0;
public int minOperations(String[] logs) {
// Call the recursive function
helper(logs, 0);
// Return the result
return depth;
}
// Write a recursive function to drill into the file system
private void helper(String[] logs, int i) {
// Set the basecase: Out of bound
if (i > logs.length - 1) return;
// Update depth base on log function string
if (logs[i].equals("../")) {
if (depth > 0) {
depth--;
}
} else if (logs[i].equals("./")) {
;
} else {
depth++;
}
// Call recursive function on next log item
helper(logs, i+1);
}
}Iterative
class Solution:
def minOperations(self, logs: List[str]) -> int:
# Create a stack
stack = []
# Add/Remove items from stack
for log in logs:
if log == "../":
if stack:
stack.pop()
elif log == "./":
continue
else:
stack.append(log)
# Return the size of stack
return len(stack)class Solution {
public int minOperations(String[] logs) {
// Create a stack
var stack = new Stack<String>();
//Add/Remove items from stack
for(var log : logs){
if(log.equals("../")){
if(!stack.empty())
stack.pop();
}else if(log.equals("./")){
}else{
stack.push(log);
}
}
// Return the size of stack.
return stack.size();
}
}Review the code by running specific example(s) and recording values (watchlist) of your code's variables along the way.
- Trace through your code with an input to check for the expected output
- Catch possible edge cases and off-by-one errors
Evaluate the performance of your algorithm and state any strong/weak or future potential work.
Assume N represents the size of array
- Time Complexity: O(N) because we will run the algorithm once to process all logged commands
- Space Complexity: O(1) because the recusive call does not need to be stored in memory. Technically this called Tail recursion, a recursion of a function where it does not consumes stack space and hence prevents stack overflow.