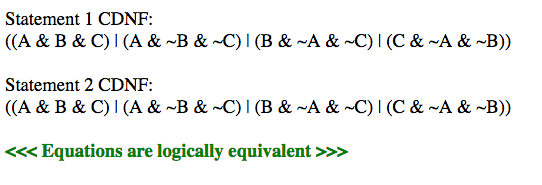We check for equivalency of two given logical formulas.
The basic outline of the program is below:
- Use the Identity, Annihilation, and Inverse laws to simplify expressions involving ⊥ and ⊤.
Note that this will either eliminate all ⊥ and ⊤’s, or one ends up with ⊥ or ⊤ as the final
statement. If the resulting statement is ⊥, then the statement is in CDNF, and we can stop.
We’ll also stop if the statement is ⊤, and A(ϕ, ψ) is empty. If the statement is ⊤, and A(ϕ, ψ) is not empty, then use Complement to replace with A ∨ ¬A where A ∈ A(ϕ, ψ), and proceed. - Put the statement into NNF by repeated applications of DeMorgan and Double Negation.
- Put the statement into DNF by repeated applications of Distribution of ∧ over ∨.
- ** Use Adjacency to ensure that every conjunction contains a literal A or ¬A for every A ∈ A(ϕ, ψ). That is: use Adjacency to ‘add’ literals that are ‘missing’ in any conjunction. E.g. if A(ϕ, ψ) ={P,Q, R}, then a conjunct such as P ∧ Q becomes (P ∧ Q ∧ R) ∨ (P ∧ Q ∧ ¬R)
- ** Use Commutation to order the conjuncts in any conjunction according to O. E.g. A ∧ B ∧ A ∧ ¬A becomes A ∧ A ∧ ¬A ∧ B
- Use Idempotence to eliminate duplicate conjuncts. E.g. A ∧ A ∧ ¬A ∧ B becomes A ∧ ¬A ∧ B
- Use Complement and Annihilation to replace any conjunction containing a literal and its negation with a contradiction symbol. E.g. A ∧ ¬A ∧ B becomes ⊥ ∧ B becomes ⊥.
- Use Identity to get rid of all disjuncts that are ⊥. If there is only one disjunct ⊥ left, then the statement is in CDNF and the process can stop.
- Use Idempotence to eliminate any duplicate disjuncts. (If didn't stop at step 8)
- Finally, use Commutation to get all disjuncts in the ‘right’ order. (If didn't stop at step 8)
It uses a functional format for inputting logical formulas. This is the base identity for inputs:
A
not(A)
and(A, B)
or(A, B)
if(A, B)
iff(A, B)
where A and B can either be atomic statements or a functional operator. All operators are either unary (not) or binary (and, or, if, iff) and there is no support for a generalized notation. This means that and(A, B, C) will thrown an error.