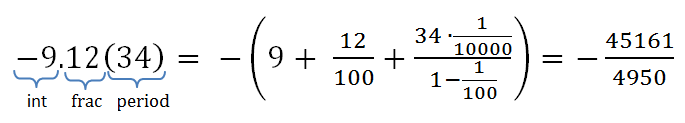MathExpressions.NET

A library for parsing math expressions with rational numbers, finding their derivatives, and compiling an optimal IL code.

Libraries

• ANTLR - Code generation from math expression grammar.
• WolframAlpha.NET - Symbolic derivatives testing.
• ILSpy - IL assembly disassembler. For compilation testing.
• NUnit - General testing purposes.

Using

Simplification

var func = new MathFunc("(2 * x ^ 2 - 1 + 0 * a) ^ -1 * (2 * x ^ 2  - 1 * 1) ^ -1").Simplify();
// func == (x ^ 2 * 2 + -1) ^ -2;

Differentiation

var func = new MathFunc("(2 * x ^ 2 - 1 + 0 * a) ^ -1 * (2 * x ^ 2  - 1 * 1) ^ -1").GetDerivative();
// func == -((x ^ 2 * 2 + -1) ^ -3 * x * 8)

Compilation

Dynamic using

using (var mathAssembly = new MathAssembly("(2 * x ^ 2 - 1 + 0 * a) ^ -1 * (2 * x ^ 2  - 1 * 1) ^ -1", "x"))
{
  var funcResult = mathAssembly.Func(5);
  // funcResult == 0.00041649312786339027 (precision value is -1/2401)
  var funcDerResult = mathAssembly.FuncDerivative(5);
  // funcDerResult == -0.00033999439009256349 (precision value is -40/117649)
}

Static using (more faster and conventional)

You should compile assembly with MathExpressions.NET and add make reference to this assembly your project. For function: (2 * x ^ 2 - 1 + 0 * a) ^ -1 * (2 * x ^ 2 - 1 * 1) ^ -1 with the variable of x, you'll get:

var funcResult = MathFuncLib.MathFunc.Func(5);
// funcResult == 0.00041649312786339027 (precision value is -1/2401)
var funcDerResult = MathFuncLib.MathFunc.FuncDerivative(5);
// funcDerResult == -0.00033999439009256349 (precision value is -40/117649)

Undefined constants and functions

using (var mathAssembly = new MathAssembly("b(x) + 10 * x * a", "x"))
{
  var b = new Func<double, double>(x => x * x);
  var funcResult = mathAssembly.Func(5, 2, b); // x = 5; a = 2; b = x ^ 2
  // funcResult == 5 ^ 2 + 10 * 5 * 2 = 125
  var funcDerResult = mathAssembly.FuncDerivative(5, 2, b); // x = 5; a = 2; b = x ^ 2
  // funcDerResult == (b(x + dx) - b(x)) / dx + 10 * a = 30
}

Types of MathNodes

• Calculated - Calculated decimal constant.
• Value - Calculated constant of Rational<long, long> format. Based on Stephen M. McKamey implementation.
• Constant - Undefined constant. It have name such as a, b etc.
• Variable - It have name, such as x, y etc.
• Function - This node present known (sin(x), log(x, 3), x + a) or unknown (a(x), b'(x)) function. It may have one or more children.

Steps of math expression processing

Parsing and AST building

Implemented with ANTLR. The output of this step is a the tree structure of MathFuncNode types, which was described above.

Rational Numbers

• Taking of symbolic derivative. This is the recursive process of replacing simple nodes without children by constants (0 and 1), taking substitutions from the table for known functions (such as for sin(x)' = cos(x)), and replacing unknown functions with themselves with stroke (I mean a(x)' = a'(x)).
  • Calculated' = Value' = Constant' = 0
  • Variable' = 1
  • KnownFunc(x)' = Derivatives[KnownFunc](x) * x'
  • UnknownFunc(x)' = UnknownFunc'(x) * x'
• Simplification. This is similar to the previous process, but with another substitution rules, such as
  • a * 1 = a
  • a + 0 = a
  • a - a = 0
  • ...

It's worth mentioning that commutative functions (addition and multiplication) taken as a function with several nodes for more easy and flexible traversers.

For properly nodes comparison, sorting is using, as demonstrated on the image below:

Compilation

At this step simplified tree from the previous step transformed to the list of IL commands. There are implemented some optimizations:

Fast exponentiation (by squaring)

At this step expression with powers converts to optimized form with exponentiation by squaring algorithm. For example: a*a*a*a*a*a will be converted to (a^2)^2 * a^2.

Using the result of previously calculated nodes

If the result of the calculated value of any function is using more than one time, it can be stored to the local variable and it can be used at further code by such way:

if (!func.Calculated)
{
    EmitFunc(funcNode);
    func.Calculated = true;
}
else
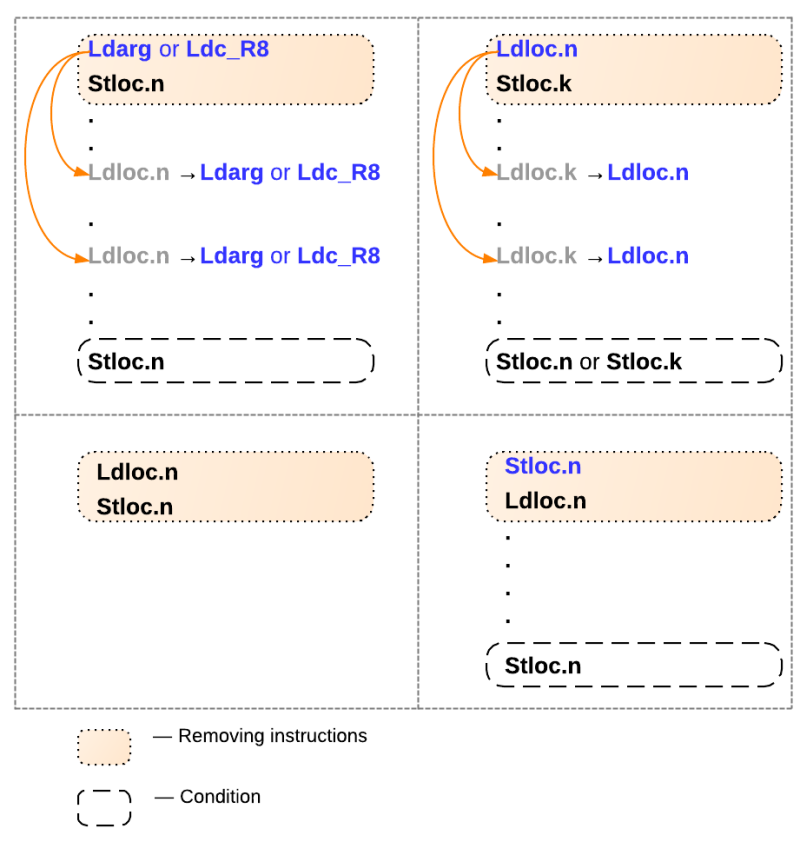
    IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));

Waste IL instruction removing

For generated IL code for math functions without loops, the following optimizations are available:

Local vars count reducing

One local variable is used for every calculated function. But it can be also used for another calculated result. So, it is possible to reduce the number of local variables by such a way:

Testing

WolframAlpha.NET

This lib for comparison of expected derivative from WolframAlpha API and actual derivative.

Assembly loading and unloading

.NET assembly has been generated on the compilation step. For dynamical assembly loading and unloading AppDomain is used with CreateInstanceFromAndUnwrap.

Comparison output of csc.exe compiler in release mode and my output

I compared generated IL code for example following function:

x ^ 3 + sin(3 * ln(x * 1)) + x ^ ln(2 * sin(3 * ln(x))) - 2 * x ^ 3

csc.exe .NET 4.5.1

MathExpressions.NET

ldarg.0 ldc.r8 3 call float64 Math::Pow(float64, float64) ldc.r8 3 ldarg.0 ldc.r8 1 mul call float64 Math::Log(float64) mul call float64 Math::Sin(float64) add ldarg.0 ldc.r8 2 ldc.r8 3 ldarg.0 call float64Math::Log(float64) mul call float64 Math::Sin(float64) mul call float64 Math::Log(float64) ldc.r8 2 ldarg.0 ldc.r83 call float64 Math::Pow(float64, float64) mul sub call float64 Math::Pow(float64, float64) add ret

ldarg.0 ldc.r8 2 ldc.r8 3 ldarg.0 call float64 Math::Log(float64) mul call float64 Math::Sin(float64) stloc.0 ldloc.0 mul call float64 Math::Log(float64) call float64 Math::Pow(float64,float64) ldarg.0 ldarg.0 mul ldarg.0 mul sub ldloc.0 add ret

More detail explanation available on Russian