-
Notifications
You must be signed in to change notification settings - Fork 10
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
about #37 and cscherrer/Soss-probprog#3
- Loading branch information
Showing
1 changed file
with
290 additions
and
0 deletions.
There are no files selected for viewing
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,290 @@ | ||
| # About GG's Capabilities | ||
|
|
||
| The term "GeneralizedGenerated", named after the generalization of Julia's [generated functions](https://docs.julialang.org/en/v1/manual/metaprogramming/#Generated-functions-1), shows its design purpose and the real world problem it solved. | ||
|
|
||
| However, as the generated functions actually belongs to an advanced meta-programming part of Julia, | ||
| for the sake of practical use, documentations and citations, we decide to write this document for giving | ||
| some non-specialist and specialist introduction to GG. | ||
|
|
||
|
|
||
| ## A Use Case for Miraculous Speed-up | ||
|
|
||
| We present here a nice example to show how generated functions and GG enable high performance computations that cannot be made in traditional programming languages of both dynamic and static ones. | ||
|
|
||
| Suppose we have a matrix, and we want to sum its biggest circle inside. | ||
|
|
||
|  | ||
|
|
||
| To simply, we use an algorithm for an approximation of this result, where a preliminary implementation can be | ||
|
|
||
| ```julia | ||
| function sum_circle(matrix::Array{F, 2}) where F | ||
| (m, n) = size(matrix) | ||
| (cx, cy) = center = ((m - 1) // 2, (n - 1) // 2) | ||
| radius = min(cx, cy) | ||
| s = zero(F) | ||
| I = Int | ||
| D = Float64 | ||
| xrange = I(cx-radius):I(cx+radius) | ||
| yrange = I(cy-radius):I(cy+radius) | ||
| radius = radius + 0.5 | ||
| for x = xrange, y = yrange | ||
| if hypot(D(cx - x), D(cy - y)) <= radius | ||
| s += matrix[x + 1, y + 1] | ||
| end | ||
| end | ||
| s | ||
| end | ||
| ``` | ||
|
|
||
| When benchmarking it, | ||
| ```julia | ||
| using LinearAlgebra | ||
| using BenchmarkTools | ||
| data = rand(Int, (25, 25)) .% 500 | ||
| julia> @btime sum_circle(data) | ||
| # Out: | ||
| 96.500 μs (1 allocation: 16 bytes) | ||
| -114514 | ||
| ``` | ||
|
|
||
| The application of generated functions to this problem is due to the possibility of statically deciding the selection of points covered by the circle. | ||
|
|
||
| Say, if we already know the row number and col number of the given matrix, we can simply generate code for above computation: | ||
|
|
||
| ```julia | ||
| I = Int | ||
| D = Float64 | ||
| # `m n` are constants now | ||
| # the name of the array is `matrix` | ||
| (cx, cy) = center = ((m - 1) // 2, (n - 1) // 2) | ||
| radius = min(cx, cy) | ||
| s = zero(F) | ||
| xrange = I(cx-radius):I(cx+radius) | ||
| yrange = I(cy-radius):I(cy+radius) | ||
| radius = radius + 0.5 | ||
| for x = xrange, y = yrange | ||
| if hypot(D(cx - x), D(cy - y)) <= radius | ||
| s = :($s + $matrix[$(x + 1), $(y + 1)]) | ||
| end | ||
| end | ||
| ``` | ||
|
|
||
| By this way, we can got an AST in the form of `0 + arr[x1, y1] + arr[x2, y2] + arr[x3, y3] + ... + arr[xn, yn]`. | ||
|
|
||
| To make this possible, we need to **type-encode** the shape of matrix. | ||
|
|
||
| Thanks to Julia's type system, integers, and other data whose memory representations are sequential, can be used as types for dispatching(dynamic and static). | ||
|
|
||
| ```julia | ||
| struct DimMatrix{M, N, F} | ||
| data :: Array{F, 2} | ||
| end | ||
| matrix = ... # rand(Float32, (2, 3)) | ||
| row, col = size(matrix) | ||
| DimMatrix{row, col, eltype(arr)}(matrix) | ||
| ``` | ||
|
|
||
| Now, I convince(**IMPORTANT**): | ||
|
|
||
| For **any valid type `F`**, given **any runtime value `arr :: Array{F, 2}`**, with a statically defined type `DimMatrix`, we can make **one** function as an amazingly fast version of `sum_circle`, which is capable of avoiding the computation of the selection for points in the circle implied by the matrix. | ||
|
|
||
| Firstly, we need to define a generator, | ||
| which accepts a `DimMatrix` **type**, and the abstract syntax tree(`matrix_ast`) for representing the runtime value of the matrix, and **return the computation logic**. | ||
|
|
||
| From the perspective of Programming Languages, it's a type-directed code generation. | ||
|
|
||
| ```julia | ||
| function sum_circle_generator(matrix_ast::Any, ::Type{DimMatrix{M, N, F}}) where {M, N, F} | ||
| I = Int | ||
| D = Float64 | ||
| (cx, cy) = center = ((M - 1) // 2, (N - 1) // 2) | ||
| radius = min(cx, cy) | ||
| s = zero(F) | ||
| xrange = I(cx-radius):I(cx+radius) | ||
| yrange = I(cy-radius):I(cy+radius) | ||
| radius = radius + 0.5 | ||
| for x = xrange, y = yrange | ||
| if hypot(D(cx - x), D(cy - y)) <= radius | ||
| s = :($s + $matrix_ast[$(x + 1), $(y + 1)]) | ||
| end | ||
| end | ||
| s | ||
| end | ||
| ``` | ||
|
|
||
| We can check it effects by some tiny data. | ||
|
|
||
| ```julia | ||
| tiny_data = rand(Int, (4, 4)) .% 100 | ||
| # Out: | ||
| 4×4 Array{Int64,2}: | ||
| 19 62 -95 -77 | ||
| 20 -72 -59 42 | ||
| 29 -70 85 -74 | ||
| -45 83 -54 40 | ||
|
|
||
| sum_circle_generator(:mat, DimMatrix{size(tiny_data)..., eltype(tiny_data)}) | ||
| # Out: | ||
| (((((((((((0 + | ||
| mat[1, 2]) + | ||
| mat[1, 3]) + | ||
| mat[2, 1]) + | ||
| mat[2, 2]) + | ||
| mat[2, 3]) + | ||
| mat[2, 4]) + | ||
| mat[3, 1]) + | ||
| mat[3, 2]) + | ||
| mat[3, 3]) + | ||
| mat[3, 4]) + | ||
| mat[4, 2]) + | ||
| mat[4, 3] | ||
| ``` | ||
|
|
||
| This is the plot of the selection of points. | ||
|
|
||
| 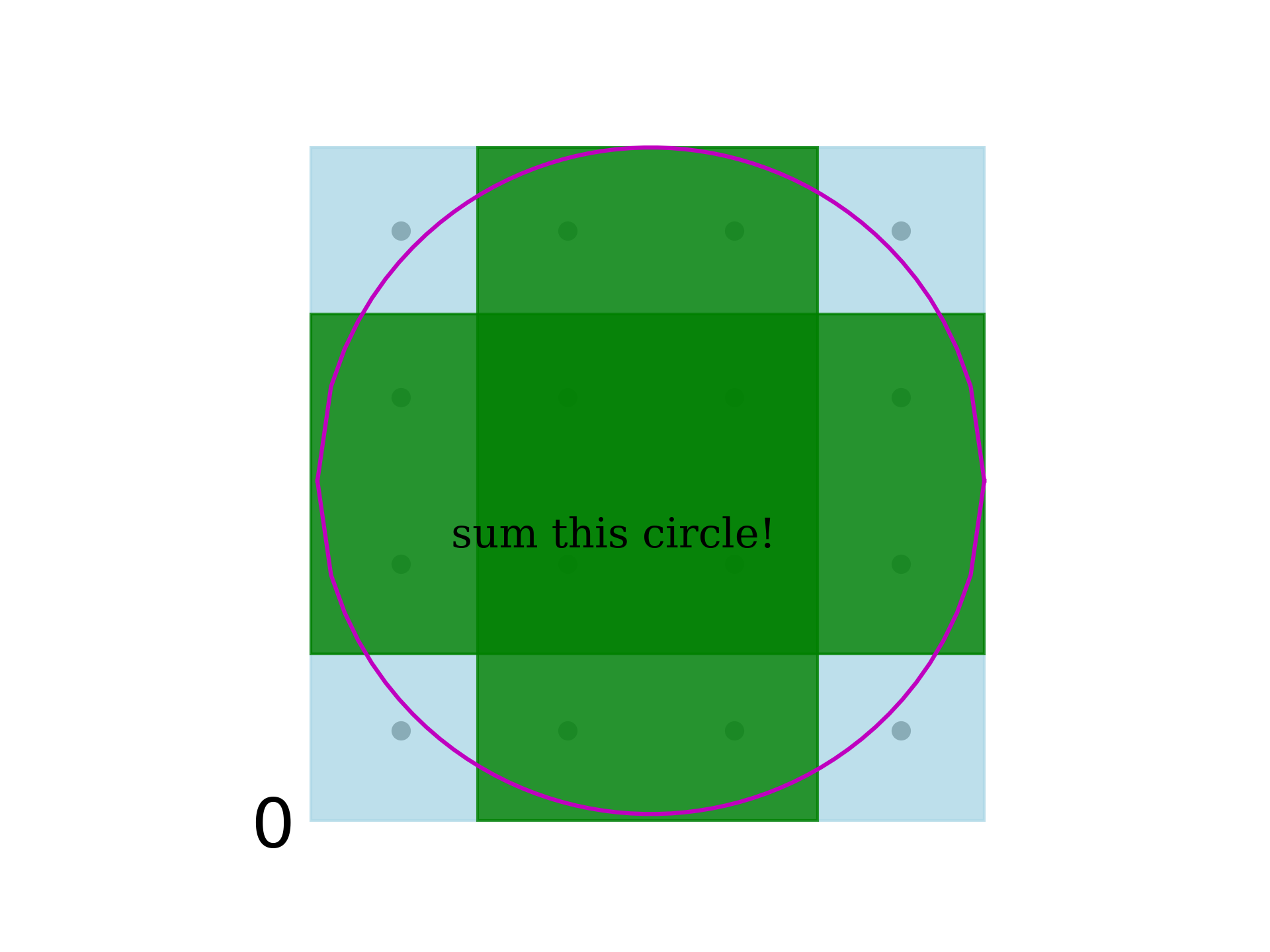 | ||
|
|
||
|
|
||
| Secondly, to execute above generated code in runtime without runtime overhead for any input `matrix`, we're supposed to use generated functions: | ||
|
|
||
| ```julia | ||
| generated_sum_circle(mat::Array{F, 2}) where F = | ||
| begin m, n = size(mat) | ||
| generated_sum_circle(DimMatrix{m, n, F}(mat)) | ||
| end | ||
|
|
||
| @generated generated_sum_circle(mat::Ty) where{ | ||
| F, M, N, Ty <: DimMatrix{M, N, F} | ||
| } = begin | ||
| @assert mat == Ty # yes! that's it! | ||
| sum_circle_generator(:(mat.data), Ty) | ||
| end | ||
| ``` | ||
|
|
||
| In a generated function, we invoke the generator, and return the generated code. Its features are: | ||
|
|
||
| - Generating code once and only for each combination of argument types | ||
| - Working perfectly with JIT compilation and type inference | ||
| - If the type is inferred in compile time, the code generated in compile time; otherwise, type inference and generated code are made in runtime. Both ways are "zero-cost", if we don't take the overhead of JIT compilation into consideration. | ||
|
|
||
| From the perspective of Programming Languages, this mechanism shows an extension to staging techniques. | ||
|
|
||
| Now, we could try our generated function as an alternative to `sum_circle`, | ||
| and **enjoy a free lunch of more than 200x performance speed-up**: | ||
|
|
||
| ```julia | ||
| # In: | ||
| @btime generated_sum_circle(data) | ||
| # Out: | ||
| 413.065 ns (2 allocations: 32 bytes) | ||
| -114515 | ||
|
|
||
|
|
||
| # polymorphic for other types: | ||
|
|
||
| # In: | ||
| data = rand(Float32, (25, 25)); | ||
| @btime sum_circle(data) | ||
| # Out: | ||
| 96.500 μs (1 allocation: 16 bytes) | ||
| 235.8246f0 | ||
|
|
||
|
|
||
| # In: | ||
| @btime generated_sum_circle(data) | ||
| # Out: | ||
| 811.616 ns (2 allocations: 32 bytes) | ||
| 235.8246f0 | ||
|
|
||
| # In: | ||
| data = data = (rand(Int, (25, 25)) .% 100) .// 100; | ||
| @btime generated_sum_circle(data) | ||
|
|
||
| # Out: | ||
| 16.399 μs (2 allocations: 48 bytes) | ||
| -277//100 | ||
|
|
||
| # In: | ||
| @btime sum_circle(data) | ||
| 123.099 μs (1 allocation: 32 bytes) | ||
| -277//100 | ||
| ``` | ||
|
|
||
|
|
||
| I have good experience with more than 30 programming languages, and this is something we essentially cannot achieve in other programming languages, until now. | ||
|
|
||
| ## Restrictions | ||
|
|
||
| Generated functions are good, but its use didn't proliferate much, which is partially affected by the restrictions of generated functions. | ||
|
|
||
| The restrictions lie in 2 aspects, compiler overhead and effectiveness restriction due to implementation. | ||
|
|
||
| ### Compiler Overhead | ||
|
|
||
| One of the problem prevents the use of generated functions is, | ||
| it burdens the compiler heavily. If number of used combinations of input parameters grows fast, you may feel there're some runtime delay caused by generated functions. | ||
|
|
||
| Triggering compilation and optimizations in runtime is a double-edged sword. | ||
|
|
||
| For instance, for the aforementioned example, the function `generated_sum_circle` cannot work for a really big matrix. | ||
|
|
||
| ```julia | ||
| data = rand(Float32, (2500, 2500)) | ||
| generated_sum_circle(data) | ||
| # Booom! | ||
| ``` | ||
|
|
||
| The direct reason for the crash of above code is, the generated code | ||
| contains a `π/4 2500 * 2500`-depth addition expressions. | ||
|
|
||
| A simple fix is to manually reduce the size of generated code, by changing the generator `sum_circle_generator`: | ||
|
|
||
| ```julia | ||
| function sum_circle_generator(matrix_ast::Any, ::Type{DimMatrix{M, N, F}}) where {M, N, F} | ||
| I = Int | ||
| D = Float64 | ||
| (cx, cy) = center = ((M - 1) // 2, (N - 1) // 2) | ||
| radius = min(cx, cy) | ||
| xrange = I(cx-radius):I(cx+radius) | ||
| yrange = I(cy-radius):I(cy+radius) | ||
| radius = radius + 0.5 | ||
| xs = Int[] | ||
| ys = Int[] | ||
| num_point = 0 | ||
| for x = xrange, y = yrange | ||
| if hypot(D(cx - x), D(cy - y)) <= radius | ||
| push!(xs, x + 1) | ||
| push!(ys, y + 1) | ||
| num_point += 1 | ||
| end | ||
| end | ||
| quote s = 0 | ||
| xs :: Vector{Int} = $xs | ||
| ys :: Vector{Int} = $ys | ||
| for i in 1:$num_point | ||
| x = xs[i] | ||
| y = ys[i] | ||
| s += $matrix_ast[x, y] | ||
| end | ||
| s | ||
| end | ||
| end | ||
|
|
||
| data = rand(Float32, (2500, 2500)) | ||
| @btime generated_sum_circle(data) | ||
| 29.645 ms (4 allocations: 64 bytes) | ||
| 2.4547852f6 | ||
|
|
||
| @btime sum_circle(data) | ||
| 1.086 s (1 allocation: 16 bytes) | ||
| 2.4547852f6 | ||
| ``` | ||
|
|
||
| However, as it's not automatically made, | ||
| it's not hard to imagine writing code in this way will be painful in some cases. | ||
|
|
||
| ### Effectiveness | ||
|
|
||
| Currently, the generated functions provided in Julia core is quite limited, and the most common case seen by users is, a generated function don't support nested functions. | ||
|
|