Topological Data Analysis (TDA) is a recent and fast growing field providing a set of new topological and geometric tools to infer relevant features for possibly complex data. Here we propose a set of notebooks for the practice of TDA with the Python Gudhi library together with popular machine learning and data sciences libraries. See for instance this paper for an introduction to TDA for data science. The complete list of notebooks can also be found at the end of this page.
See the installation page or if you have conda you can make a conda install.
TDA typically aims at extracting topological signatures from a point
cloud in
or in a general metric space. By studying the topology
of a point cloud, we actually mean studying the topology of the unions
of balls centered at the point cloud, also called offsets. However,
non-discrete sets such as offsets, and also continuous mathematical
shapes like curves, surfaces and more generally manifolds, cannot easily
be encoded as finite discrete structures. Simplicial
complexes are
therefore used in computational geometry to approximate such shapes.
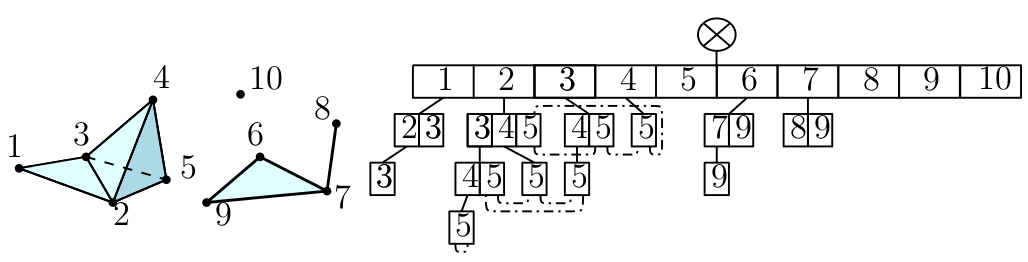
A simplicial complex is a set of simplices, they can be seen as higher dimensional generalization of graphs. These are mathematical objects that are both topological and combinatorial, a property making them particularly useful for TDA. The challenge here is to define such structures that are proven to reflect relevant information about the structure of data and that can be effectively constructed and manipulated in practice. Below is an exemple of simplicial complex:
A filtration is an increasing sequence of sub-complexes of a simplicial
complex
. It can be seen as ordering the simplices included in
the complex
. Indeed, simpicial complexes often come with a specific
order, as for Vietoris-Rips
complexes,
Cech complexes and
alpha
complexes.
Notebook: Simplex trees. In Gudhi, filtered simplicial complexes are encoded through a data structure called simplex tree. Vertices are represented as integers, edges as pairs of integers, etc.
Notebook: Vietoris-Rips complexes and alpha complexes from data
points. In
practice, the first step of the TDA Analysis Pipeline is to define a
filtration of simplicial complexes for some data. This notebook explains
how to build Vietoris-Rips complexes and alpha complexes (represented as
simplex trees) from data points in
, using the simplex tree data structure.
Notebook: Rips and alpha complexes from pairwise distance. It is also possible to define Rips complexes in general metric spaces from a matrix of pairwise distances. The definition of the metric on the data is usually given as an input or guided by the application. It is however important to notice that the choice of the metric may be critical to reveal interesting topological and geometric features of the data. We also give in this last notebook a way to define alpha complexes from matrix of pairwise distances by first applying a multidimensional scaling (MDS) transformation on the matrix.
TDA signatures can extracted from point clouds but in many cases in data sciences the question is to study the topology of the sublevel sets of a function.
Above is an example for a function defined on a subset of
but in general the function
is defined on a subset
of
.
Notebook: cubical complexes. One
first approach for studying the topology of the sublevel sets of a
function is to define a regular grid on
and then to define a filtered complex based on this
grid and the function
.
Homology is a well-known concept in algebraic topology. It provides a
powerful tool to formalize and handle the notion of topological features
of a topological space or of a simplicial complex in an algebraic way.
For any dimension , the
-dimensional holes are
represented by a vector space
, whose dimension
is intuitively the number of such independent features. For example, the
-dimensional homology
group
represents
the connected components of the complex, the
-dimensional homology
group
represents
the
-dimensional loops,
the
-dimensional
homology group
represents the
-dimensional cavities and so on.
Persistent homology is a powerful tool to compute, study and encode efficiently multiscale topological features of nested families of simplicial complexes and topological spaces. It encodes the evolution of the homology groups of the nested complexes across the scales. The diagram below shows several level sets of the filtration:
Notebook: persistence diagrams In this notebook we show how to compute barcodes and persistence diagrams from a filtration defined on the Protein binding dataset. This tutorial also introduces the bottleneck distance between persistence diagrams.
In this notebook, we learn how to use alternative representations of persistence with the representations module and finally we see a first example of how to efficiently combine machine learning and topological data analysis.
This notebook illustrates the notion of “Expected Persistence Diagram”, which is a way to encode the topology of a random process as a deterministic measure.
For many applications of persistent homology, we observe topological features close to the diagonal. Since they correspond to topological structures that die very soon after they appear in the filtration, these points are generally considered as “topological noise”. Confidence regions for persistence diagram provide a rigorous framework to this idea. This notebook introduces the subsampling approach of Fasy et al. 2014 AoS.
C. Oballe and V. Maroulas provide a tutorial for a Python module that implements the model for Bayesian inference with persistence diagrams introduced in their paper.
Two libraries related to Gudhi:
- ATOL: Automatic Topologically-Oriented Learning. See this tutorial.
- Perslay: A Simple and Versatile Neural Network Layer for Persistence Diagrams. See this tutorial.
This notebook introduces the distance to measure (DTM) filtration, as defined in this paper. This filtration can be used for robust TDA. The DTM can also be used for robust approximations of compact sets, see this notebook.
In this notebook, we will see how Gudhi and Tensorflow can be combined to perform optimization of persistence diagrams to solve an inverse problem. This other, less complete notebook shows that this kind of optimization works just as well with PyTorch.
Vietoris-Rips complexes and alpha complexes from data points
Visualizing simplicial complexes
Rips and alpha complexes from pairwise distance
Persistence diagrams and bottleneck distance
Representations of persistence
Confidence regions for persistence diagrams - data points
Confidence regions with Bottleneck Bootstrap
Inverse problem and optimization with TDA
PyTorch differentiation of diagrams
Contact : [email protected]