JavaScript 实现数据结构与算法
难度简单68收藏分享切换为英文接收动态反馈
写一个 RecentCounter 类来计算特定时间范围内最近的请求。
请你实现 RecentCounter 类:
RecentCounter()初始化计数器,请求数为 0 。int ping(int t)在时间t添加一个新请求,其中t表示以毫秒为单位的某个时间,并返回过去 3000 毫秒内发生的所有请求数(包括新请求)。确切地说,返回在[t-3000, t]内发生的请求数。
保证每次对 ping 的调用都使用比之前更大的 t 值。
示例 1:
输入:
["RecentCounter", "ping", "ping", "ping", "ping"]
[[], [1], [100], [3001], [3002]]
输出:
[null, 1, 2, 3, 3]
解释:
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = [1],范围是 [-2999,1],返回 1
recentCounter.ping(100); // requests = [<u>1</u>, <u>100</u>],范围是 [-2900,100],返回 2
recentCounter.ping(3001); // requests = [<u>1</u>, <u>100</u>, <u>3001</u>],范围是 [1,3001],返回 3
recentCounter.ping(3002); // requests = [1, <u>100</u>, <u>3001</u>, <u>3002</u>],范围是 [2,3002],返回 3提示:
1 <= t <= 104- 保证每次对
ping的调用都使用比之前更大的t值 - 至多调用
ping方法104次
通过次数18,683
提交次数25,945
var RecentCounter = function() {
this.queue = [];
};
/**
* @param {number} t
* @return {number}
*/
RecentCounter.prototype.ping = function(t) {
this.queue.push(t);
while (this.queue[0] < t - 3000) {
this.queue.shift();
}
return this.queue.length;
};
/**
* Your RecentCounter object will be instantiated and called as such:
* var obj = new RecentCounter()
* var param_1 = obj.ping(t)
*/难度简单778收藏分享切换为英文接收动态反馈
请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点。传入函数的唯一参数为 要被删除的节点 。
现有一个链表 -- head = [4,5,1,9],它可以表示为:
示例 1:
输入:head = [4,5,1,9], node = 5
输出:[4,1,9]
解释:给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.示例 2:
输入:head = [4,5,1,9], node = 1
输出:[4,5,9]
解释:给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.提示:
- 链表至少包含两个节点。
- 链表中所有节点的值都是唯一的。
- 给定的节点为非末尾节点并且一定是链表中的一个有效节点。
- 不要从你的函数中返回任何结果。
通过次数134,360
提交次数161,578
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} node
* @return {void} Do not return anything, modify node in-place instead.
*/
var deleteNode = function(node) {
node.val = node.next.val;
node.next = node.next.next;
};难度简单1287收藏分享切换为英文接收动态反馈
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL进阶: 你可以迭代或递归地反转链表。你能否用两种方法解决这道题?
通过次数352,126
提交次数497,910
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
console.log(head,'head')
let p1 = head;
let p2 = null;
while (p1) {
console.log(p1,'我是p1===========》')
const tmp = p1.next;
console.log(tmp,'我是tmp')
p1.next = p2;
console.log(p1,'我是p1改变之后=====》')
p2 = p1;
p1 = tmp;
}
return p2;
};难度中等5110收藏分享切换为英文接收动态反馈
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807通过次数597,843
提交次数1,543,436
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
var addTwoNumbers = function(l1, l2) {
const l3 = new ListNode(0);
let p1 = l1;
let p2 = l2;
let p3 = l3;
let carry = 0;
while (p1 || p2) {
const v1 = p1 ? p1.val : 0;
const v2 = p2 ? p2.val : 0;
const val = v1 + v2 + carry;
carry = Math.floor(val / 10);
p3.next = new ListNode(val % 10);
if (p1) p1 = p1.next;
if (p2) p2 = p2.next;
p3 = p3.next;
console.log(l3, 'l3=======0900000')
console.log(p3, 'p3=======0800000')
}
if( carry ) {
p3.next = new ListNode(carry);
}
return l3.next;
};难度简单413收藏分享切换为英文接收动态反馈
给定一个排序链表,删除所有重复的元素,使得每个元素只出现一次。
示例 1:
输入: 1->1->2
输出: 1->2示例 2:
输入: 1->1->2->3->3
输出: 1->2->3通过次数150,560
提交次数291,739
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var deleteDuplicates = function(head) {
let p = head;
while (p && p.next) {
if (p.val === p.next.val) {
p.next = p.next.next
} else {
p = p.next;
}
}
return head;
};难度简单829收藏分享切换为英文接收动态反馈
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。提示:
- 链表中节点的数目范围是
[0, 104] -105 <= Node.val <= 105pos为-1或者链表中的一个 有效索引 。
通过次数273,283
提交次数543,745
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
var hasCycle = function(head) {
let p1 = head;
let p2 = head;
while (p1 && p2 && p2.next) {
p1 = p1.next;
p2 = p2.next.next;
if (p1 === p2) {
return true;
}
}
return false
};难度简单240收藏分享切换为英文接收动态反馈
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
说明:
- 输出结果中的每个元素一定是唯一的。
- 我们可以不考虑输出结果的顺序。
通过次数98,926
提交次数139,409
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
//方法一:
// var intersection = function(nums1, nums2) {
// return [...new Set(nums1)].filter(n => nums2.includes(n))
// };
// 方法二:
var intersection = function(nums1, nums2) {
const map = new Map();
nums1.forEach(n => {
map.set(n, true)
})
const res = [];
nums2.forEach(n => {
if(map.get(n)) {
res.push(n);
map.delete(n)
}
})
return res;
};难度简单1924收藏分享切换为英文接收动态反馈
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: "()"
输出: true示例 2:
输入: "()[]{}"
输出: true示例 3:
输入: "(]"
输出: false示例 4:
输入: "([)]"
输出: false示例 5:
输入: "{[]}"
输出: true通过次数436,165
提交次数1,011,029
/**
* @param {string} s
* @return {boolean}
*/
// var isValid = function(s) {
// if(s.length % 2 === 1) {
// return false;
// }
// const stack = [];
// for (i = 0; i < s.length; i++) {
// const c = s[i];
// if (c === '(' || c === '{' || c === '[') {
// stack.push(c);
// } else {
// const t = stack[stack.length - 1];
// if (
// (t === '(' && c === ')') ||
// (t === '{' && c === '}') ||
// (t === '[' && c === ']')
// ) {
// stack.pop();
// } else {
// return false;
// }
// }
// }
// return stack.length === 0;
// };
//优化后的
var isValid = function(s) {
if(s.length % 2 === 1) {
return false;
}
const stack = [];
const map = new Map();
map.set('(', ')');
map.set('[', ']');
map.set('{', '}');
for (i = 0; i < s.length; i++) {
const c = s[i];
if (map.has(c)) {
stack.push(c);
} else {
const t = stack[stack.length - 1];
if (map.get(t) === c) {
stack.pop();
} else {
return false;
}
}
}
return stack.length === 0;
};难度简单9389收藏分享切换为英文接收动态反馈
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
通过次数1,473,821
提交次数2,965,004
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
const map = new Map();
for (let i = 0; i < nums.length; i++) {
const n = nums[i];
const n2 = target - n;
if (map.has(n2)) {
return [map.get(n2), i]
} else {
map.set(n, i)
}
}
};难度中等4476收藏分享切换为英文接收动态反馈
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。通过次数696,833
提交次数1,948,213
/**
* @param {string} s
* @return {number}
*/
var lengthOfLongestSubstring = function(s) {
let l = 0;
let res = 0;
const map = new Map();
for (let r = 0; r < s.length; r++) {
if (map.has(s[r]) && map.get(s[r]) >= l) {
l = map.get(s[r]) + 1;
}
res = Math.max(res, r - l + 1);
map.set(s[r], r);
}
return res;
};难度困难793收藏分享切换为英文接收动态反馈
给你一个字符串 S、一个字符串 T 。请你设计一种算法,可以在 O(n) 的时间复杂度内,从字符串 S 里面找出:包含 T 所有字符的最小子串。
示例:
输入:S = "ADOBECODEBANC", T = "ABC"
输出:"BANC"提示:
- 如果 S 中不存这样的子串,则返回空字符串
""。 - 如果 S 中存在这样的子串,我们保证它是唯一的答案。
通过次数84,273
提交次数213,812
/**
* @param {string} s
* @param {string} t
* @return {string}
*/
var minWindow = function(s, t) {
let l = 0;
let r = 0;
const need = new Map();
for (let c of t) {
need.set(c, need.has(c) ? need.get(c) + 1 : 1)
}
let needType = need.size;
let res = '';
while (r < s.length) {
const c = s[r];
if(need.has(c)) {
need.set(c, need.get(c) - 1)
if(need.get(c) === 0) needType -= 1;
}
while(needType === 0) {
const newRes = s.substring(l, r + 1);
if (!res || newRes.length < res.length) {
res = newRes;
}
const c2 = s[l];
if (need.has(c2)) {
need.set(c2, need.get(c2) + 1)
if(need.get(c2) === 1) needType += 1;
}
l += 1;
}
r++;
}
return res;
};难度简单721收藏分享切换为英文接收动态反馈
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回它的最大深度 3 。
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
let res = 0;
const dfs = (n, l) => {
if (!n) { return }
if (!n.left && !n.right) {
res = Math.max(res, l)
}
dfs(n.left, l + 1);
dfs(n.right,l + 1);
};
dfs(root, 1);
return res;
};难度简单383收藏分享切换为英文接收动态反馈
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回它的最小深度 2.
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
if (!root) {
return 0;
}
const q = [[root, 1]];
while (q.length) {
const [n, l] = q.shift();
if (!n.left && !n.right) {
return l;
}
if (n.left) {
q.push([n.left,l + 1]);
}
if (n.right) {
q.push([n.right,l + 1]);
}
}
}难度中等671收藏分享切换为英文接收动态反馈
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function(root) {
if (!root) {
return [];
}
const q = [[root, 0]];
const res = [];
while (q.length) {
const [n, level] = q.shift();
if (!res[level]) {
res.push([n.val]);
} else {
res[level].push(n.val)
}
if (n.left) {
q.push([n.left, level + 1]);
}
if (n.right) {
q.push([n.right, level + 1]);
}
}
return res;
};
法二:
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
// var levelOrder = function(root) {
// if (!root) {
// return [];
// }
// const q = [[root, 0]];
// const res = [];
// while (q.length) {
// const [n, level] = q.shift();
// if (!res[level]) {
// res.push([n.val]);
// } else {
// res[level].push(n.val)
// }
// if (n.left) {
// q.push([n.left, level + 1]);
// }
// if (n.right) {
// q.push([n.right, level + 1]);
// }
// }
// return res;
// };
//法二:
var levelOrder = function(root) {
if (!root) {
return [];
}
const q = [root];
const res = [];
while(q.length) {
let len = q.length;
res.push([]);
while(len--) {
const n = q.shift();
res[res.length - 1].push(n.val);
if(n.left) {
q.push(n.left)
}
if(n.right) {
q.push(n.right)
}
}
}
return res;
}难度中等751收藏分享切换为英文接收动态反馈
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
通过次数285,017
提交次数385,849
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
// var inorderTraversal = function(root) {
// const res = [];
// const rec = (n) => {
// if(!n) {
// return
// }
// rec(n.left);
// res.push(n.val);
// rec(n.right);
// }
// rec(root);
// return res;
// };
// 法二:
var inorderTraversal = function(root) {
const res = [];
const stack = [];
let p = root;
while (stack.length || p) {
while (p) {
stack.push(p);
p = p.left;
}
const n = stack.pop();
res.push(n.val);
p = n.right;
}
return res;
}难度简单447收藏分享切换为英文接收动态反馈
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {number} sum
* @return {boolean}
*/
var hasPathSum = function(root, sum) {
if(!root) return false;
let res = false;
const dfs = (n, s) => {
if (!n.left && !n.right && s === sum) {
res = true;
}
if (n.left) dfs(n.left, s + n.left.val)
if (n.right) dfs(n.right, s + n.right.val)
}
dfs(root, root.val);
return res;
};!(README.assets/image-20201021154244543.png)
难度困难158收藏分享切换为英文接收动态反馈
验证给定的字符串是否可以解释为十进制数字。
例如:
"0"` => `true`
`" 0.1 "` => `true`
`"abc"` => `false`
`"1 a"` => `false`
`"2e10"` => `true`
`" -90e3 "` => `true`
`" 1e"` => `false`
`"e3"` => `false`
`" 6e-1"` => `true`
`" 99e2.5 "` => `false`
`"53.5e93"` => `true`
`" --6 "` => `false`
`"-+3"` => `false`
`"95a54e53"` => `false说明: 我们有意将问题陈述地比较模糊。在实现代码之前,你应当事先思考所有可能的情况。这里给出一份可能存在于有效十进制数字中的字符列表:
- 数字 0-9
- 指数 - "e"
- 正/负号 - "+"/"-"
- 小数点 - "."
当然,在输入中,这些字符的上下文也很重要。
更新于 2015-02-10:
C++函数的形式已经更新了。如果你仍然看见你的函数接收 const char * 类型的参数,请点击重载按钮重置你的代码。
通过次数19,661
提交次数93,309
/**
* @param {string} s
* @return {boolean}
*/
var isNumber = function(s) {
const graph = {
0: { 'blank': 0, 'sign': 1, '.': 2, 'digit': 6},
1: { 'digit': 6, '.': 2},
2: { 'digit': 3},
3: { 'digit': 3, 'e': 4},
4: { 'digit': 5, 'sign': 7},
5: { 'digit': 5},
6: { 'digit': 6, '.': 3, 'e': 4},
7: { 'digit': 5},
};
let state = 0;
for (c of s.trim()) {
if (c >= '0' && c <= '9') {
c = 'digit';
} else if (c === ' ') {
c = 'blank';
} else if (c === '+' || c === '-') {
c = 'sign';
}
state = graph[state][c];
if (state === undefined) {
return false;
}
}
if (state === 3 || state === 5 || state === 6) {
return true;
}
return false;
};难度中等162收藏分享切换为英文接收动态反馈
给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界,而“大西洋”处于大陆的右边界和下边界。
规定水流只能按照上、下、左、右四个方向流动,且只能从高到低或者在同等高度上流动。
请找出那些水流既可以流动到“太平洋”,又能流动到“大西洋”的陆地单元的坐标。
提示:
- 输出坐标的顺序不重要
- m 和 n 都小于150
示例:
给定下面的 5x5 矩阵:
太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5) *
~ 3 2 3 (4) (4) *
~ 2 4 (5) 3 1 *
~ (6) (7) 1 4 5 *
~ (5) 1 1 2 4 *
* * * * * 大西洋
返回:
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).通过次数12,543
提交次数28,983
/**
* @param {number[][]} matrix
* @return {number[][]}
*/
var pacificAtlantic = function(matrix) {
// 矩阵无值或不是二维
if (!matrix || !matrix[0]) return [];
const row = matrix.length;
const column = matrix[0].length;
// 记录能流到太平洋的坐标
const flowT = Array.from({length: row}, () => new Array(column).fill(false));
// 记录能流到大西洋的坐标
const flowD = Array.from({length: row}, () => {
return new Array(column).fill(false);
});
// console.log(row,column,flowT,flowD);
// 深度优先遍历 (r,c) 当前节点的坐标 flow:flowT/flowD
const dfs = (r, c, flow) => {
flow[r][c] = true;
// 遍历相邻节点,上下左右四个节点
[[r-1,c],[r+1,c],[r,c-1],[r,c+1]].forEach(([nextR,nextC]) => {
if(
// 保证节点在矩阵中
nextR >= 0 && nextR < row &&
nextC >= 0 && nextC < column &&
// 防止死循环,保证之前没访问该节点
!flow[nextR][nextC] &&
// 保证逆流而上
matrix[nextR][nextC] >= matrix[r][c]
){
dfs(nextR, nextC, flow);
}
});
};
// 沿着海岸线逆流而上
for(let i = 0; i < row; i++){
// 第1列
dfs(i, 0, flowT);
// 最后1列
dfs(i, column - 1, flowD);
}
for(let j = 0; j < column; j++){
// 第一行
dfs(0, j, flowT);
// 最后一行
dfs(row - 1, j, flowD);
}
// 收集能流到两个大洋的坐标
const res = [];
for (let r = 0; r < row; r++){
for(let c = 0; c < column; c++){
if(flowT[r][c] && flowD[r][c]){
res.push([r,c]);
}
}
}
return res;
};难度中等276
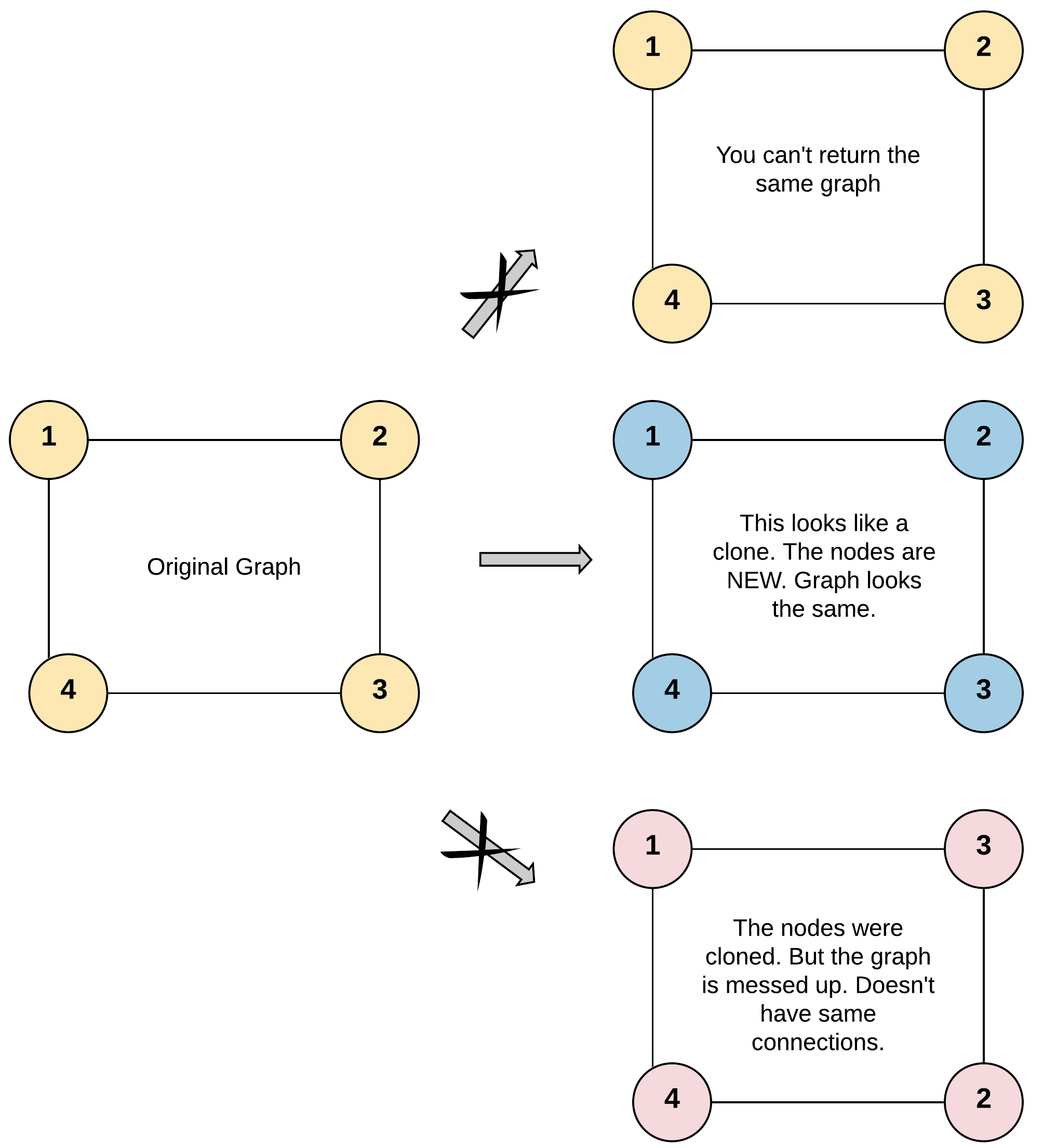
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;
}测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。示例 2:
输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。示例 4:
输入:adjList = [[2],[1]]
输出:[[2],[1]]提示:
- 节点数不超过 100 。
- 每个节点值
Node.val都是唯一的,1 <= Node.val <= 100。 - 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
- 图是连通图,你可以从给定节点访问到所有节点。
通过次数49,327
提交次数75,764
/**
* // Definition for a Node.
* function Node(val, neighbors) {
* this.val = val === undefined ? 0 : val;
* this.neighbors = neighbors === undefined ? [] : neighbors;
* };
*/
/**
* @param {Node} node
* @return {Node}
*/
// //深度优先遍历
// var cloneGraph = function(node) {
// if (!node) {
// return
// }
// const visited = new Map();
// const dfs = (n) => {
// const nCopy = new Node(n.val);
// visited.set(n, nCopy);
// (n.neighbors || []).forEach(ne => {
// if(!visited.has(ne)) {
// dfs(ne);
// }
// nCopy.neighbors.push(visited.get(ne))
// })
// }
// dfs(node);
// return visited.get(node);
// };
//广度优先遍历
var cloneGraph = function(node) {
if (!node) {
return
}
const visited = new Map();
visited.set(node, new Node(node.val));
const q = [node];
while(q.length) {
const n = q.shift();
(n.neighbors || []).forEach(ne => {
if (!visited.has(ne)) {
q.push(ne);
visited.set(ne, new Node(ne.val));
}
visited.get(n).neighbors.push(visited.get(ne));
})
}
return visited.get(node);
};难度中等753
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5示例 2:
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4说明:
你可以假设 k 总是有效的,且 1 ≤ k ≤ 数组的长度。
通过次数214,696
提交次数333,381
class MinHeap {
constructor() {
this.heap = [];
}
swap(i1, i2) {
const temp = this.heap[i1];
this.heap[i1] = this.heap[i2];
this.heap[i2] = temp;
}
getParentIndex(i) {
return (i - 1) >> 1;
}
getLeftIndex(i) {
return i * 2 + 1;
}
getRightIndex(i) {
return i * 2 + 2;
}
shiftUp(index) {
if (index == 0) { return }
const parentIndex = this.getParentIndex(index);
if (this.heap[parentIndex] > this.heap[index]) {
this.swap(parentIndex, index);
this.shiftUp(parentIndex)
}
}
shiftDown(index) {
const leftIndex = this.getLeftIndex(index);
const rightIndex = this.getRightIndex(index);
if (this.heap[leftIndex] < this.heap[index]) {
this.swap(leftIndex, index);
this.shiftDown(leftIndex)
}
if (this.heap[rightIndex] < this.heap[index]) {
this.swap(rightIndex, index);
this.shiftDown(rightIndex)
}
}
insert(value) {
this.heap.push(value);
this.shiftUp(this.heap.length - 1);
}
pop() {
this.heap[0] = this.heap.pop();
this.shiftDown(0);
}
peek() {
return this.heap[0];
}
size() {
return this.heap.length;
}
}
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var findKthLargest = function(nums, k) {
const h = new MinHeap();
nums.forEach(n => {
h.insert(n);
if(h.size() > k) {
h.pop();
}
})
return h.peek();
};难度中等549
给定一个非空的整数数组,返回其中出现频率前 *k* 高的元素。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
- 你可以假设给定的 k 总是合理的,且 1 ≤ k ≤ 数组中不相同的元素的个数。
- 你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
- 题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的。
- 你可以按任意顺序返回答案。
通过次数112,091
提交次数181,666
class MinHeap {
constructor() {
this.heap = [];
}
swap(i1, i2) {
const temp = this.heap[i1];
this.heap[i1] = this.heap[i2];
this.heap[i2] = temp;
}
getParentIndex(i) {
return (i - 1) >> 1;
}
getLeftIndex(i) {
return i * 2 + 1;
}
getRightIndex(i) {
return i * 2 + 2;
}
shiftUp(index) {
if (index == 0) { return }
const parentIndex = this.getParentIndex(index);
if (this.heap[parentIndex] && this.heap[parentIndex].value > this.heap[index].value) {
this.swap(parentIndex, index);
this.shiftUp(parentIndex)
}
}
shiftDown(index) {
const leftIndex = this.getLeftIndex(index);
const rightIndex = this.getRightIndex(index);
if (this.heap[leftIndex] && this.heap[leftIndex].value < this.heap[index].value) {
this.swap(leftIndex, index);
this.shiftDown(leftIndex)
}
if (this.heap[rightIndex] && this.heap[rightIndex].value < this.heap[index].value) {
this.swap(rightIndex, index);
this.shiftDown(rightIndex)
}
}
insert(value) {
this.heap.push(value);
this.shiftUp(this.heap.length - 1);
}
pop() {
this.heap[0] = this.heap.pop();
this.shiftDown(0);
}
peek() {
return this.heap[0];
}
size() {
return this.heap.length;
}
}
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
// var topKFrequent = function(nums, k) {
// const map = new Map();
// nums.forEach(n => {
// map.set(n, map.has(n) ? map.get(n) + 1 : 1);
// })
// //该方法不满足你的算法的时间复杂度必须优于 O(n log n) , n 是数组的大小。
// const list = Array.from(map).sort((a, b) => b[1] - a[1]);
// return list.slice(0, k).map(n => n[0]);
// };
var topKFrequent = function(nums, k) {
const map = new Map();
nums.forEach( n => {
map.set(n, map.has(n) ? map.get(n) + 1 : 1)
})
const h = new MinHeap();
map.forEach((value, key) => {
h.insert({value,key})
if(h.size() > k) {
h.pop();
}
})
return h.heap.map(a => a.key)
}难度困难964
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6示例 2:
输入:lists = []
输出:[]示例 3:
输入:lists = [[]]
输出:[]提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
通过次数180,740
提交次数338,131
class MinHeap {
constructor() {
this.heap = [];
}
swap(i1, i2) {
const temp = this.heap[i1];
this.heap[i1] = this.heap[i2];
this.heap[i2] = temp;
}
getParentIndex(i) {
return (i - 1) >> 1;
}
getLeftIndex(i) {
return i * 2 + 1;
}
getRightIndex(i) {
return i * 2 + 2;
}
shiftUp(index) {
if (index == 0) { return }
const parentIndex = this.getParentIndex(index);
if (this.heap[parentIndex] && this.heap[parentIndex].val > this.heap[index].val) {
this.swap(parentIndex, index);
this.shiftUp(parentIndex)
}
}
shiftDown(index) {
const leftIndex = this.getLeftIndex(index);
const rightIndex = this.getRightIndex(index);
if (this.heap[leftIndex] && this.heap[leftIndex].val < this.heap[index].val) {
this.swap(leftIndex, index);
this.shiftDown(leftIndex)
}
if (this.heap[rightIndex] && this.heap[rightIndex].val < this.heap[index].val) {
this.swap(rightIndex, index);
this.shiftDown(rightIndex)
}
}
insert(value) {
this.heap.push(value);
this.shiftUp(this.heap.length - 1);
}
pop() {
if(this.size() === 1) return this.heap.shift();
const top = this.heap[0];
this.heap[0] = this.heap.pop();
this.shiftDown(0);
return top;
}
peek() {
return this.heap[0];
}
size() {
return this.heap.length;
}
}
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode[]} lists
* @return {ListNode}
*/
var mergeKLists = function(lists) {
const res = new ListNode(0);
let p = res;
const h = new MinHeap();
lists.forEach(l => {
l && h.insert(l)
})
while(h.size()) {
const n = h.pop();
p.next = n;
p = p.next;
n.next && h.insert(n.next);
}
return res.next;
};// 实现数组中两项(索引i/j)的交换
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
return arr;
}
Array.prototype.bubble = function bubble() {
// this -> ary
let _this = this,
flag = false;
// 控制循环多少轮
for (let i = 0; i < _this.length - 1; i++) {
// 控制每一轮循环多少次
for (let j = 0; j < _this.length - 1 - i; j++) {
// 交换位置
if (_this[j] > _this[j + 1]) {
swap(_this, j, j + 1);
flag = true;
}
}
if (!flag) break;
flag = false;
}
return _this;
};
let ary = [12, 8, 24, 16, 1];
ary.bubble();
console.log(ary); Array.prototype.selectionSort = function() {
for ( let i = 0; i < this.length - 1; i++) {
let indexMin = i;
for (j = i; j < this.length; j++) {
if (this[j] < this[indexMin]) {
indexMin = j;
}
}
if (indexMin !== i) {
const temp = this[i];
this[i] = this[indexMin];
this[indexMin] = temp;
}
}
}
const arr = [5, 4, 3, 2, 1];
arr.selectionSort()Array.prototype.insertionSort = function () {
for (let i = 0; i < this.length; i++) {
const temp = this[i];
let j = i;
while (j > 0) {
if (this[j - 1] > temp) {
this[j] = this[j - 1];
} else {
break;
}
j--;
}
this[j] = temp;
}
}
const arr = [5, 4, 3, 2, 1];
arr.insertionSort()Array.prototype.mergeSort = function () {
const rec = (arr) => {
if (arr.length === 1) {
return arr;
}
const mid = Math.floor(arr.length / 2);
const left = arr.slice(0, mid);
const right = arr.slice(mid, arr.length);
const orderLeft = rec(left);
const orderRight = rec(right);
const res = [];
while (orderLeft.length || orderRight.length) {
if (orderLeft.length && orderRight.length) {
res.push(orderLeft[0] < orderRight[0] ? orderLeft.shift() : orderRight.shift())
} else if (orderLeft.length) {
res.push(orderLeft.shift())
} else if (orderRight.length) {
res.push(orderRight.shift())
}
}
return res;
}
const res = rec(this);
res.forEach((n, i) => {
this[i] = n;
})
}
const arr = [5, 4, 3, 2, 1];
arr.mergeSort()Array.prototype.quickSort = function () {
const rec = (arr) => {
if (arr.length === 1) {
return arr;
}
const left = [];
const right = [];
const mid = arr[0];
for (let i = 1; i < arr.length; i++) {
if (arr[i] < mid) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return [...rec(left), mid, ...rec(right)]
};
const res = rec(this);
res.forEach((n, i) => {
this[i] = n;
});
}
const arr = [2, 4, 5, 3, 1];
arr.quickSort()
console.log(arr) Array.prototype.sequentialSearch = function (item) {
for (let i = 0; i < this.length; i++) {
if (this[i] === item) {
return i;
}
}
return -1;
};
const res = [1, 2, 3, 4, 5].sequentialSearch(3);
console.log(res) Array.prototype.binarySearch = function (item) {
let low = 0;
let high = this.length - 1;
while (low <= high) {
const mid = Math.floor((low + high) / 2);
const element = this[mid];
if (element < item) {
low = mid + 1;
} else if (element > item) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
};
const res = [1, 2, 3, 4, 5].binarySearch(3);
console.log(res)难度简单1343
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
通过次数396,621
提交次数614,219
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
var mergeTwoLists = function (l1, l2) {
const res = new ListNode(0);
let p = res;
let p1 = l1;
let p2 = l2;
while (p1 && p2) {
if (p1.val < p2.val) {
p.next = p1;
p1 = p1.next;
} else {
p.next = p2;
p2 = p2.next;
}
p = p.next;
}
if (p1) {
p.next = p1;
}
if (p2) {
p.next = p2;
}
return res.next;
};难度简单88
猜数字游戏的规则如下:
- 每轮游戏,我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
- 如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。
你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果,返回值一共有 3 种可能的情况(-1,1 或 0):
- -1:我选出的数字比你猜的数字小
pick < num - 1:我选出的数字比你猜的数字大
pick > num - 0:我选出的数字和你猜的数字一样。恭喜!你猜对了!
pick == num
示例 1:
输入:n = 10, pick = 6
输出:6示例 2:
输入:n = 1, pick = 1
输出:1示例 3:
输入:n = 2, pick = 1
输出:1示例 4:
输入:n = 2, pick = 2
输出:2提示:
1 <= n <= 231 - 11 <= pick <= n
通过次数34,852
提交次数75,652
/**
* Forward declaration of guess API.
* @param {number} num your guess
* @return -1 if num is lower than the guess number
* 1 if num is higher than the guess number
* otherwise return 0
* var guess = function(num) {}
*/
/**
* @param {number} n
* @return {number}
*/
var guessNumber = function (n) {
let low = 1;
let high = n;
while (low <= high) {
const mid = Math.floor((low + high) / 2);
const res = guess(mid);
if (res === 0) {
return mid;
} else if (res === 1) {
low = mid + 1;
} else {
high = mid - 1
}
}
};/**
* Forward declaration of guess API.
* @param {number} num your guess
* @return -1 if num is lower than the guess number
* 1 if num is higher than the guess number
* otherwise return 0
* var guess = function(num) {}
*/
/**
* @param {number} n
* @return {number}
*/
// var guessNumber = function (n) {
// let low = 1;
// let high = n;
// while (low <= high) {
// const mid = Math.floor((low + high) / 2);
// const res = guess(mid);
// if (res === 0) {
// return mid;
// } else if (res === 1) {
// low = mid + 1;
// } else {
// high = mid - 1
// }
// }
// };
//分而治之方法解
var guessNumber = function (n) {
const rec = (low, high) => {
if (low > high) { return; }
const mid = Math.floor((low + high) / 2);
const res = guess(mid);
if (res === 0) {
return mid;
} else if (res === 1) {
return rec(mid + 1, high)
} else {
return rec(1, mid - 1)
}
};
return rec(1, n);
}226. 翻转二叉树(分而治之)
难度简单667
翻转一棵二叉树。
示例:
输入:
4
/ \
2 7
/ \ / \
1 3 6 9输出:
4
/ \
7 2
/ \ / \
9 6 3 1备注: 这个问题是受到 Max Howell 的 原问题 启发的 :
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var invertTree = function (root) {
if (!root) {
return null;
}
return {
val: root.val,
left: invertTree(root.right),
right: invertTree(root.left),
}
};100. 相同的树(分而治之)
难度简单492
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入: 1 1
/ \ / \
2 3 2 3
[1,2,3], [1,2,3]
输出: true示例 2:
输入: 1 1
/ \
2 2
[1,2], [1,null,2]
输出: false示例 3:
输入: 1 1
/ \ / \
2 1 1 2
[1,2,1], [1,1,2]
输出: false通过次数149,948
提交次数249,110
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} p
* @param {TreeNode} q
* @return {boolean}
*/
var isSameTree = function (p, q) {
if (!p && !q) {
return true;
}
if (p && q && p.val === q.val &&
isSameTree(p.left, q.left) &&
isSameTree(p.right, q.right)
) {
return true;
}
return false;
};例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3进阶:
你可以运用递归和迭代两种方法解决这个问题吗?
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function (root) {
if (!root) {
return true;
}
const isMirror = (l, r) => {
if (!l && !r) {
return true;
}
if (l && r && l.val === r.val &&
isMirror(l.left, r.right) &&
isMirror(l.right, r.left)
) {
return true
}
return false;
}
return isMirror(root.left, root.right)
};70. 爬楼梯(动态规划)
难度简单1303
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
**注意:**给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
通过次数306,812
提交次数604,494
/**
* @param {number} n
* @return {number}
*/
// var climbStairs = function (n) {
// if (n < 2) {
// return 1;
// }
// const dp = [1, 1];
// for (let i = 2; i <= n; i++) {
// dp[i] = dp[i - 1] + dp[i - 2];
// }
// console.log(dp)
// return dp[n]
// };
//优化后的代码
var climbStairs = function (n) {
if (n < 2) {
return 1;
}
let dp0 = 1;
let dp1 = 1;
for (let i = 2; i <= n; i += 1) {
const temp = dp0;
dp0 = dp1;
dp1 = dp1 + temp;
}
return dp1;
};难度简单1133
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。提示:
0 <= nums.length <= 1000 <= nums[i] <= 400
通过次数201,287
提交次数429,127
/**
* @param {number[]} nums
* @return {number}
*/
var rob = function (nums) {
if (nums.length === 0) {
return 0;
}
const dp = [0, nums[0]];
for (let i = 2; i <= nums.length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
}
return dp[nums.length];
};优化后的
/**
* @param {number[]} nums
* @return {number}
*/
// var rob = function (nums) {
// if (nums.length === 0) {
// return 0;
// }
// const dp = [0, nums[0]];
// for (let i = 2; i <= nums.length; i++) {
// dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
// }
// return dp[nums.length];
// };
//优化后的
var rob = function (nums) {
if (nums.length === 0) {
return 0;
}
const dp = [0, nums[0]];
let dp0 = 0;
let dp1 = nums[0];
for (let i = 2; i <= nums.length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i - 1], dp[i - 1]);
const dp2 = Math.max(dp0 + nums[i - 1], dp1);
dp0 = dp1;
dp1 = dp2;
}
return dp1;
};难度简单210
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
通过次数58,505
提交次数104,455
/**
* @param {number[]} g
* @param {number[]} s
* @return {number}
*/
var findContentChildren = function (g, s) {
const sortFunc = function (a, b) {
return a - b;
}
g.sort(sortFunc);
s.sort(sortFunc);
let i = 0;
s.forEach(n => {
if (n >= g[i]) {
i++
}
})
return i;
};难度简单894
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。提示:
1 <= prices.length <= 3 * 10 ^ 40 <= prices[i] <= 10 ^ 4
通过次数233,261
提交次数366,143
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function (prices) {
let profit = 0;
for (let i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
profit += prices[i] - prices[i - 1]
}
}
return profit;
};难度中等962
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]通过次数210,783
提交次数273,500
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function (nums) {
const res = [];
const backtrack = (path) => {
if (path.length === nums.length) {
res.push(path);
return;
}
nums.forEach(n => {
if (path.includes(n)) {
return
}
backtrack(path.concat(n))
})
}
backtrack([])
return res;
};难度中等855
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
**说明:**解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]通过次数164,342
提交次数207,591
/**
* @param {number[]} nums
* @return {number[][]}
*/
var subsets = function (nums) {
const res = [];
const backtrack = (path, l, start) => {
if (path.length === l) {
res.push(path);
return;
}
for (let i = start; i < nums.length; i++) {
backtrack(path.concat(nums[i]), l, i + 1)
}
}
for (let i = 0; i <= nums.length; i++) {
backtrack([], i, 0)
}
return res;
};79. 单词搜索给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board = [ ['A','B','C','E'], ['S','F','C','S'], ['A','D','E','E'] ]
给定 word = "ABCCED", 返回 true 给定 word = "SEE", 返回 true 给定 word = "ABCB", 返回 false
提示:
board 和 word 中只包含大写和小写英文字母。
1 <= board.length <= 200 1 <= board[i].length <= 200 1 <= word.length <= 10^3 通过次数119,042提交次数272,268
/**
* @param {character[][]} board
* @param {string} word
* @return {boolean}
*/
var exist = function (board, word) {
// 判断⼀些边界条件
if (board.length === 0) return false
if (word.length === 0) return true
const row = board.length
const col = board[0].length
// 每个字⺟都可以是起点
for (let i = 0; i < row; i++) {
for (let j = 0; j < col; j++) {
const ret = find(i, j, 0)
if (ret) return true
}
}
return false
function find(i, j, cur) {
//越界
if (i >= row || i < 0) return false
if (j >= col || j < 0) return false
const letter = board[i][j]
// 终⽌条件
if (letter !== word[cur]) return false
// 找到最后⼀个了
if (cur == word.length - 1) return true
// 找下⼀步
// 设置标记
board[i][j] = null
// 递归 怎么找下⼀步
const ret = find(i + 1, j, cur + 1) ||
find(i - 1, j, cur + 1) ||
find(i, j + 1, cur + 1) ||
find(i, j - 1, cur + 1)
// 取消标记 进⾏别的路线查找
board[i][j] = letter
return ret
}
};