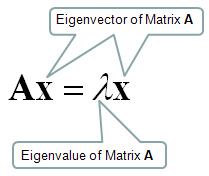Table of Contents:
- Vectors
- Linear Combinations, span and basis of vectors
- Linear transformations and matrices
- Matrix Multiplication as composition
- Determinant
- System of linear equations
- Inverse Matrices
- Rank
- Non Square Matrices
- Dot Product
- Cross Product
- Change of Basis
- Eigenvectors and eigenvalues
- Abstract Vector Spaces
Vectors are entities having both magnitude and direction. These can be represented by ordered list of numbers.
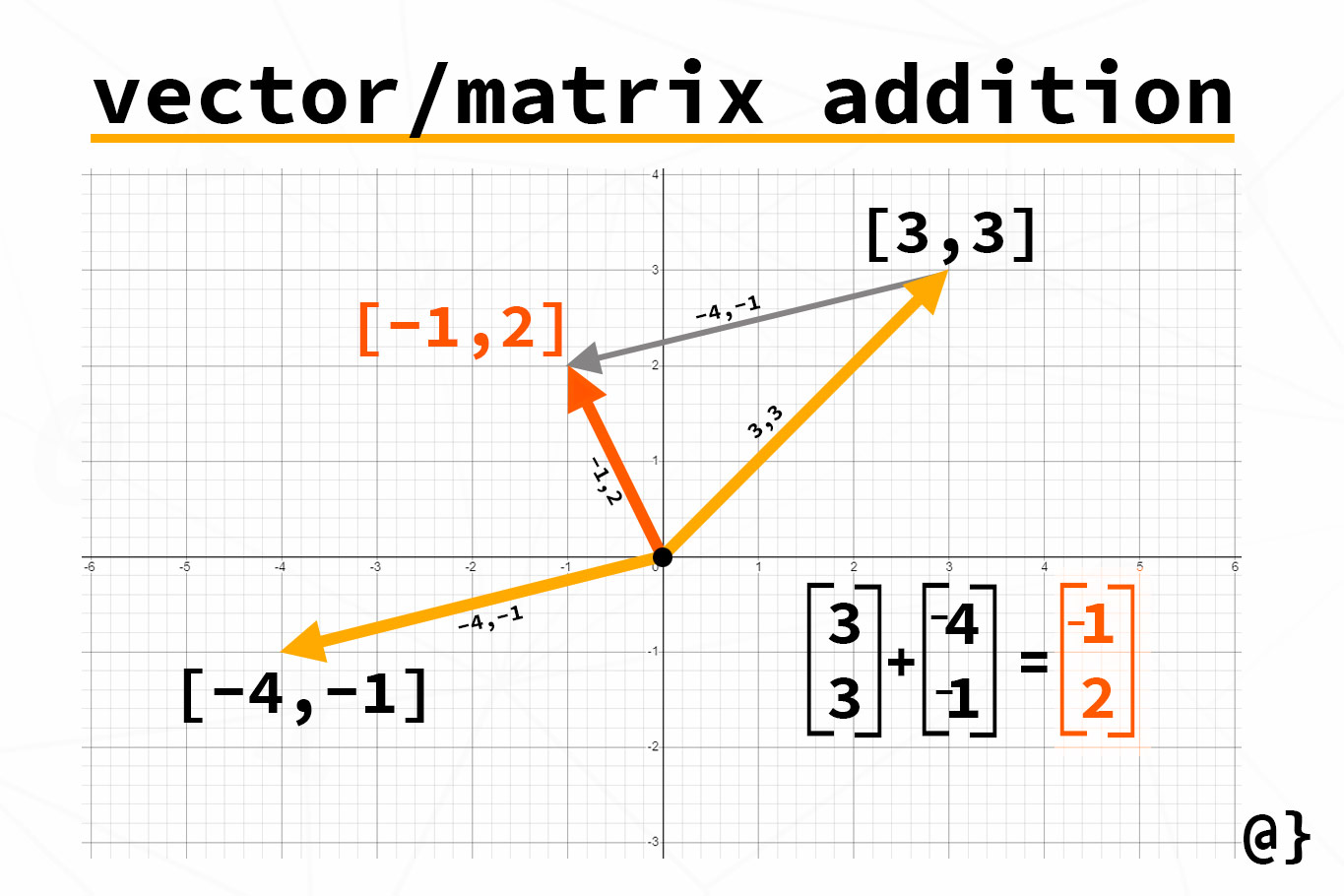
Vector Addition
Scalar Product
If you take a set of matrices, you multiply each of them by a scalar, and you add together all the products thus obtained, then you obtain a linear combination.
All the matrices involved in a linear combination need to have the same dimension (otherwise matrix addition would not be possible).
The span of a set of vectors is the set of all linear combinations of the vectors
For example, if A and B are concurrent and non-collinear vectors of same dimension then, span of their linear combinations will be complete plane on which they lie.
If A and B are collinear then the span becomes a line.
Consider linear combination xA + yB + zC, where A, B and C are vectors and x, y, z are scalar variables. If one of these vectors lies on the span of other two then it is linearly dependent. Then span will be plane formed by those two vectors.
If no vector lies on span of other two vectors, then they all are linearly independent vectors.
We can write a vector in form A = ai + bj + ck, where i, j and k are basis of space i.e they are linearly independent vectors which span the full space.
Transformations change the landing position of input vector.
Linear transformations are those in which origin is fixed and lines remain parallel and evenly spaced.
In geometric terms, it is combined effect caused by ordered transformation.
It is associative but not cummulative. Meanining
A(BC) = (AB)C, but
ABC != BAC
Determinant is scale by which any area(in case of 2D) or volume(in case of 3D)changes after transformation.
Negative determinant signifies that the orientation of plane has been reveresed.
A system of linear equations is a collection of one or more linear equations involving the same variables.
Inverse of a matrix is a matrix which reverses the transformations caused due to matrix.
Rank is the number of dimensions in output of transofrmation. If rank is equal to columns in matrix, then it is called full rank.
when rank is less than number of columns, a set of vectors will fall to origin. This set of vectors is called "Null Space" or "Kernel".
Non square matrices can change the number of dimensions after transformation. For example a 3x2 matrix will transform 3D space to a 2D space.
Dot product is the multiplication of a length of one vector and length of projection of another vector on it.
Mathematically dot product of two vectors can be given as follows
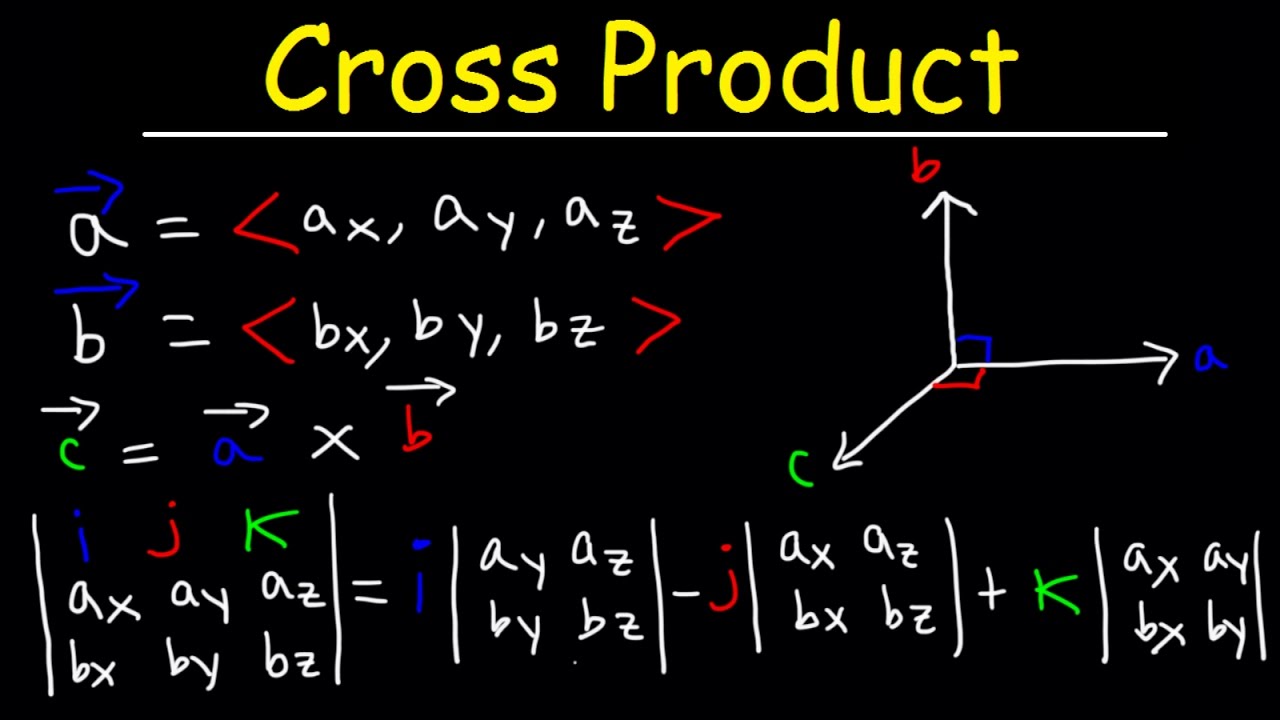
Cross product is the magnitude of the area of parallelogram formed by two vectors. It can also be represented as determinant of the matrix formed by the two vectors. Similar to determinant, the negative sign of cross product signifies that the orientation was fliped during transformation.
Change of basis is a technique applied to finite-dimensional vector spaces in order to rewrite vectors in terms of a different set of basis elements.
During linear transformation vectors get knocked off span. But some vectors remain on their own span. These vectors are known as Eigenvectors of that transformation.
Eigenvalue is factor by which the eigenvectors get streched or squished during transformation.
For a 3D space, eigenvector is the axis of rotation during transformation.
When the basis of space also become eigenvectors, then the corresponding transformation matrix becomes a diagonal matrix, where the diagonal values are eigenvalues.
Any form of data can be represented as vector as long as it follows the rules for vector adding and scaling (Axioms). All the concepts of linear algebra can be applied to such abstract vector spaces.