집합에 대하여 조금 이야기해볼 시간입니다. 수학자들에게 집합 이론은 사랑과 증오의 대상이였습니다. 그것은 수학에있어 어셈블리 언어나 마찬가지였습니다. 카테고리 이론은 집합 이론에서 멀어지려고 합니다. 예를들어 모든 집합의 집합은 존재하지 않습니다. 하지만 Set이라는 모든 카테고리들의 범주는 존재합니다. 반대로 카테고리에서 대상간 존재하는 모든 사상들이 집합을 형성한다고 가정할 수 있습니다. 심지어 이를 홈셋이라 부릅니다. 공정하게 말하면 사상들이 집합을 이루지 않는 범주 이론의 한 분야가 있습니다. 대신 이들은 다른 카테고리의 대상들입니다. 이 카테고리에서는 홈셋 대신에 홈 오브젝트다 사용되고 풍성한 범주(enriched categories.)라 부릅니다. 그러나 이제부터는 구식 홈셋이 있는 카테고리를 사용하는것을 고수할 것 입니다.
집합은 카테고리적인 대상 외부에서 얻을 수 있는 특징없는 덩어리?(blob)에 가장 가깝습니다. 집합은 원소가 있지만 이에 대하여 자세히 말할 수 없습니다. 유한한 집합이 있다면 이를 셀 수 있습니다. 무한한 집합도 cardinal numbers를 이용하여 카운팅과 비슷하게 할 수 있습니다. 예를들어 두 집합의 크기는 모두 무한하지만 자연수 집합은 실수집합보다 작습니다. 하지만 놀랍게도 유리수 집합은 자연수 집합과 같은 크기를 지닙니다..?
그 외에 모든 집합에 대한 정보는 이들간의 함수로 인코딩 될 수 있습니다. - 특별히 역이 존재하는 동형사상으로 말입니다. 모든 의도와 목적이 동형인 집합은 동일합니다. 수학자들의 노여움을 사기전에 동등과 동형(equality and isomorphism)이 근본적으로 중요하다는 것을 설명하겠습니다. 사실 이것은 최신 수학 분야의 주요 관심사 중 하나입니다.(Homotopy Type Theory (HoTT).) HoTT는 계산(computation)에서 영감을 얻은 순수한 수학적 이론이기때문에 이를 언급하겠습니다. 그리고 주요 발의자 중 한명인 Vladimir Voevodsky는 Coq 정리를 증명하며 연구하는동안 큰 깨달음을 얻었습니다. 수학과 프로그래밍의 상호작용은 쌍방으로 진행됩니다.
집합에서 중요한 교훈은 원소들과 다르게 집합은 비교해도 괜찮다는 점 입니다. 예를들어 집합은 그냥 집합이기에 특정 자연변환의 집합이 어떤 사상들의 집합과 동형이라 말할 수 있습니다. 이경우 동형은 모든 자연변환이 하나의 집합을 이루고 이간에 유일한 사상과 역의 사상이 존재한다는 것을 뜻합니다. 이들은 쌍을 이룰 수 있습니다. 만일 사과와 오렌지가 다른 카테고리에 속한다면 이 둘을 비교할 수 없습니다. 하지만 사과 집합과 오렌지 집합은 이들은 단지 집합이기에 비교를 할 수 있습니다. 종종 카테고리적인 문제를 집합이론으로 변환하는것은 우리에게 필요한 통찰력과 귀중한 정리를 증명할 수 있는 기회를 줍니다.
모든 카테고리에는 Set에 대한 표준 매핑 패밀리가 장착되어 있습니다. 사실상 이 매핑은 펑터입니다. 그렇기에 이들은 카테고리의 구조를 보존합니다. 예를들어봅시다.
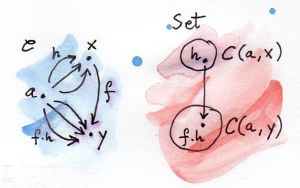
카테고리 C 에 속하는 대상 a, x가 있습니다. Hom-set C(a, x)는 집합이므로 Set의 한 대상입니다. x가 가변적이고 a가 고정되어있을때 C(a, x) 또한 Set에서 가변적일것 입니다. 그러므로 x -> Set으로 가는 하나의 매핑을 얻었습니다.
두번째 인수에 대한 hom-set을 매핑하는것을 강조하고 싶다면 다음과같이 C(a, -)로 표기방식을 사용하기도 합니다.
대상에 대한 이 매핑은 사상으로 확장될 수 있습니다. C의 임의의 대상 x, y사이에 사상 f가 있습니다. 앞서 정의한 매핑에 따라 x는 C(a, x)로 y는 C(a, y)로 매핑됩니다. 이 매핑이 펑터가 되기 위하여 f는 두셋간에 다음과 같은 함수가 되어야 합니다: C(a, x) -> C(a, y)
모든 아규먼트를 분리적으로 생각해 이 함수를 포인트 단위로 정의해봅시다. C(a, x)의 임의의 원소 h가 있습니다. 사상은 끝점이 일치한다면 합성이 가능합니다. h의 끝은 f의 시작점과 일치하기에 다음과 같이 합성됩니다.
f . h :: a -> y이는 a에서 y로 가는 사상이기에 C(a, y)의 멤버 입니다.
C(a, x)에서 C(a, y)로 향하는 함수를 찾아냈습니다. 그리고 이것은 f의 이미지를 제공합니다. 이 리프팅된 함수를 C(a, f)로 쓰겠고 h에 대한 동작은 다음과 같습니다.
C(a, f) h = f . h이 construction은 모든 카테고리에서 작동해야하기 떄문에 모든 하스켈 타입들의 카테고리에도 작동하여야합니다. 하스켈에서 홈펑터는 Reader 펑터로 더 잘 알려져 있습니다.
type Reader a x = a -> x
instance Functor (Reader a) where
fmap f h = f . hhom-set의 소스를 고정하는것 대신에 타겟을 고정하면 어떤일이 일어나는지 봅시다. 다시말해 C(-, a)도 펑터냐는것 입니다. 그렇습니다. 하지만 이는 공변이 아니라 반변입니다. 그리고 C(a, -)와 반대로 f가 이후에 합성됩니다.
이와같은 반변 펑터를 하스켈에서 이미 보았습니다. -> Op입니다.
type Op a x = x -> a
instance Contravariant (Op a) where
contramap f h = h . f만일 C(-, =) 처럼 두가지가 다 가변인경우에는 첫번째 어규먼트에 대하여 반변이고 두번째에 대해서는 공변입니다. 이와같은 profunctor를 함자성(functoriality)을 이야기하며 이미 보았었습니다.
instance Profunctor (->) where
dimap ab cd bc = cd . bd . ab
lmap = flip (.)
rmap = (.)여기서 중요한 교훈은 이 관찰(observation)이 모든 카테고리에 적용된다는 것 입니다. 대상에서 홈셋으로의 매핑은 펑터적 입니다. 반변은 반대의 카테고리에서의 매핑과 동일하기에 이 사실을 다음과 같이 간결하게 표현할 수 있습니다.
C(-, =) :: Cop X C -> SetC에 속한 어느 대상 a를 고른다하여도 C에서 Set으로 향하는 펑터가 있다는 것을 보았습니다. 이와같이 Set으로의 구조를 유지하는 매핑을 종종 표현(representation)이라 부릅니다. C의 대상과 사상을 Set에서 집합과 함수로 나타내었습니다.
펑터 C(a, -)은 그 자체로 종종 표현가능(representable) 이라 불립니다. 더 일반적으로는 모든 펑터 선택된 a에 대해 hom-functor와 자연적으로 동형인 모든 펑터 F를 표현가능이라고 합니다. 이런 펑터는 C(a, -) 이므로 반드시 Set 의 값 이여야합니다?(Such a functor must necessarily be 𝐒𝐞𝐭-valued, since 𝐂(𝑎, −) is.)
위에서 동형집합은 동일하게 생각한다고 언급했었습니다. 더 일반적으로 카테고리의 동형 대상이 동일하다고 생각합니다. 그 이유는 대상은 사상을 통하여 다른 대상과의 관계를 제외하고는 구조가 없기 때문입니다.
예를들어 일전에 우리는 처음에 집합에 의해 모델링된 모노이드의 카테고리 Mon에 대하여 이야기 했었습니다. 허나 여기서 집합의 monoidal 구조를 유지할 수 있는 함수만을 사상으로 선택하는데 주의를 기울였습니다. 그러기에 Mon에 속한 두 대상이 동형이라 함은 두 대상 사이에 역이 존재하는 사상이 존재하고 둘을 같은 구조라는 것 입니다. 기반이되는 집합과 함수를 살펴보면 한 모노이드의 단위 원소는 다른 모노이드의 다른 원소로 매핑되는것을 볼 수 있고 이 두 원소의 곱은 이들의 매핑의 곱으로 매핑됩니다.
동일한 추론이 펑터에도 적용됩니다. 두 카테고리간의 펑터는 자연변환이 사상의 역할을 하는 카테고리를 형성합니다. 그러기에 두 펑터가 동형이고 동일하다 판단될 수 있으면 이는 이 펑터 사이에 뒤집을 수 있는 자연변환이 존재함을 의미합니다.
이 관점에서 표현가능한 펑터의 정의를 분석해 봅시다. F가 표현가능한 펑터가 되기 위해선 다음이 필요합니다(F가 C(a, -)와 동형임을 보이기 위해): C에 속한 대상 a와 C(a, −) 에서 F 로 향하는 자연변환 α가 있고 반대방향의 자연변환 β, 그리고 이둘의 합성은 단위 자연변환(identity natural transformation) 입니다.
특정 x에 대한 α의 요소를 봅시다, 이는 Set에 속한 함수입니다.
alpha_x :: C(a, x) -> Fxnaturality condition에 의하여 x에서 y로 향하는 모든 사상 f는 다음의 다이어그램 commute를 따라야 함을 말합니다.
F f . alpha_x = alpha_y . C(a, f)하스켈에서 자연변환을 다형성 함수로 바꿀수 있습니다.
alpha :: forall x. (a -> x) -> F x
fmap f . alpha = alpha . fmap f매개 변수로 인해 naturality condition이 자연적으로 충족됩니다.(앞서 언급한 무료 이론(theorems for free) 중 하나입니다.) 왼편의 fmap은 펑터 F에 대하여 정의되어있고 오른쪽은 러더 펑터에 의해 정의되어있습니다. 리더펑터의 fmap은 함수의 앞서 합성하므로 더 분명해 질 수 있습니다. C(a, x)의 원소 h에 대하여 작동하는 naturality condition은 다음과 같이 단순화 할 수 있습니다.
fmap f (alpha h) = alhpha (f . h)역 방향의 변환 beta는 다음과 같습니다.
beta :: forall x. F x -> (a -> x)베타는 naturality condition를 다라야 하고 alpha의 역 이여야 합니다.
alpha . beta = id = beta . alpha조만단 C(a, -)에서 만들어진 자연변환에 Set-valued functor가 언제나 존재함을 볼것이고(Yoneda’s lemma) 하지만 항상 뒤집을 필요는 없음을 볼것입니다.
a를 Int로 list 펑터로 하스켈에서 예를 들어 보겠습니다.
alpha :: forall x. (Int -> x) -> [x]
alpha h = map h [12]임의의 숫자 12를 골랐고 이를 이용하여 싱글톤 리스트를 만들었습니다. 이후에 h를 fmap을 이용하여 리스트에 적용하였고 결과는 h의 리턴타입과 같은 리스트입니다.
naturality condition은 map의 합성과 같습니다(list 버전의 fmap)
map f (map h [12]) = map (f . h) [12]
-- 만일 역방향의 변환을 찾는다면 임의의 타입 x 리스트에서 x를 반환하는 함수로 이동해야합니다.
beta :: forall x. [x] -> (Int -> x)위는 예를들어 head를 사용하여 목록에서 x를 얻어내는것을 생각할 수 있습니다. 하지만 이는 빈 리스트에 대해서는 동작하지 않을것 입니다. 그렇기에 리스트 펑터는 표현 가능하지 않습니다.
하스켈의 (엔도) 펑터가 컨테이너와 비슷한 역할을 한다고 했던것을 기억하세요. 이를 표현가능한 펑터에서도 함수의 호출 결과를 메모라이징 하는 컨테이너로 생각할 수 있습니다(하스켈에서 hom-set의 멤버는 단지 함수이기 때문에). C(a, -)에서 표현가능한 대상 a는 키 타입으로 간주됩니다. 이를 이용하여 테뷸레이트된(tabulated) 함수값에 접근합니다. alpha라 이름지었던 변환은 tabulate라 하고 이것의 역 베터는 index라 불립니다. 다음은 단순화한 Representable 클래스 정의입니다.
class Representable f where
type Rep f :: *
tabulate :: (Rep f -> x) -> f x
index :: f x -> Rep f -> x표현 가능한 타입 a는 여기서 Rep f로 불리는것을 주목하세요. 이는 표현가능함의 정의의 일부입니다. Rep f는 단지 타입입니다.(as opposed to a type constructor, or other more exotic kinds).
비어있지않은 무한 리스트, 스트림은 모두 표현 가능합니다.
data Stream x = Cons x (Stream x)이를 인수를 취하는 함수의 기억된 리턴값으로 생각할 수 있습니다.
이 함수를 tabulate 하기 위해서는 무한한 스트림값을 만들어야합니다. 하스켈은 lazy하기 때문에 가능합니다. 값은 필요시에만 평가될것이고 이 메모라이즈된 값을 index를 이용하여 접근할 수 있습니다.
instance Representable Stream where
type Repo Stream = Integer
tabulate f = Cons (f 0) (tabulate (f . (+1)))
index (Cons b bs) n = if n == 0 then b else index bs (n-1)하나의 메로라이제이션 체계를 이용하여 임의의 리턴타입에 대한 함수들을 커버할 수 있다는 점이 흥미롭습니다.
표현가능한 반변 펑터는 쉽게 정의할 수 있습니다. C(-, a)에서 두번째 아규먼트를 고정시키면 됩니다. 혹은 동등하게도 Cop -> Set으로 향하는 펑터를 생각하면 됩니다. Cop(a, -)는 C(-, a)와 같기때문입니다.
표현가능함을 약간 변형할 수 있습니다. hom-set이 Cartesian closed categories에서 내부적으로 exponential objects으로 취급되었던것을 기억하세요. Hom-set C(a, x)는 x^a와 동일합니다. 그리고 표현가능한 펑터 F는 다음과 같이 쓸 수 있습니다: -^a = F
이에 양변에 로그를 취해봅시다: a = logF
이는 물론 단지 형식적인 변환이지만 로그의 속성 중 일부를 알고있다면 매우 유용합니다. 특히 product 타입을 기반으로 하는 펑터는 sum타입으로 표현될 수 있습니다. 그리고 sum타입의 펑터는 일반적으로 표현가능하지 않습니다(ex: list functor)
마지막으로 표현가능한 펑터는 우리에게 함수와 데이터 구조라는 다른 종류의 구현을 제공합니다. 그들은 정확히 동일한 내용을 지니고 있도 동일한 키를 이용하여 값이 검색됩니다. 그것이 제가 말했던 "동일성"의 의미입니다. 두개의 자연스러운 동형 펑터는 그들의 내용이 포함되는한 동일합니다(Two naturally isomorphic functors are identical as far as their contents are involved.) 반면에 두 표현가능함은 종종 다르게 구현될 수 있고 다른 퍼포먼스적인 특징을 지닙니다. 메모라이제이션은 퍼포먼스 향상에 쓰일 수 있고 이는 런타임을 충분히 줄여줍니다. 동일한 기본 계산의 다른 표현을 생성할 수 있다는 점은 매우 중요합니다. 그래서 놀랍게도 퍼포먼스적인 측면만 생각하는것을 제외하고도 카테고리 이론은 실질적인 가치가 있는 대체 구현을 탐색할 수 있는 충분한 기회를 제공합니다.