Skip to content

Latest commit

 

History

History
210 lines (171 loc) · 6.51 KB

README.md

File metadata and controls

210 lines (171 loc) · 6.51 KB

2371. Minimize Maximum Value in a Grid

English Version

题目描述

You are given an m x n integer matrix grid containing distinct positive integers.

You have to replace each integer in the matrix with a positive integer satisfying the following conditions:

  • The relative order of every two elements that are in the same row or column should stay the same after the replacements.
  • The maximum number in the matrix after the replacements should be as small as possible.

The relative order stays the same if for all pairs of elements in the original matrix such that grid[r1][c1] > grid[r2][c2] where either r1 == r2 or c1 == c2, then it must be true that grid[r1][c1] > grid[r2][c2] after the replacements.

For example, if grid = [[2, 4, 5], [7, 3, 9]] then a good replacement could be either grid = [[1, 2, 3], [2, 1, 4]] or grid = [[1, 2, 3], [3, 1, 4]].

Return the resulting matrix. If there are multiple answers, return any of them.

 

Example 1:

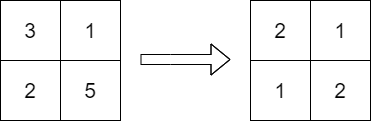
Input: grid = [[3,1],[2,5]]
Output: [[2,1],[1,2]]
Explanation: The above diagram shows a valid replacement.
The maximum number in the matrix is 2. It can be shown that no smaller value can be obtained.

Example 2:

Input: grid = [[10]]
Output: [[1]]
Explanation: We replace the only number in the matrix with 1.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 105
  • 1 <= grid[i][j] <= 109
  • grid consists of distinct integers.

解法

方法一：排序 + 贪心

由于可以将每一个数字重新填入并且使最终矩阵的最大值最小化，可考虑贪心。

矩阵中每一个数字不一样，可考虑哈希表或数组记录每个数字对应的位置。

将所有数字排序。然后从小到大填入新的数字，每次填入的数字为当前行和列的较大值再加一，同时用新填入的数字更新当前行和列的最大值。

时间复杂度 $O(mn\log mn)$，空间复杂度 $O(mn)$。其中 $m$ 和 $n$ 是矩阵的行数和列数。

Python3

class Solution:
    def minScore(self, grid: List[List[int]]) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        nums = [(v, i, j) for i, row in enumerate(grid)
                for j, v in enumerate(row)]
        nums.sort()
        row_max = [0] * m
        col_max = [0] * n
        ans = [[0] * n for _ in range(m)]
        for _, i, j in nums:
            ans[i][j] = max(row_max[i], col_max[j]) + 1
            row_max[i] = col_max[j] = ans[i][j]
        return ans

Java

class Solution {
    public int[][] minScore(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        List<int[]> nums = new ArrayList<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                nums.add(new int[]{grid[i][j], i, j});
            }
        }
        Collections.sort(nums, (a, b) -> a[0] - b[0]);
        int[] rowMax = new int[m];
        int[] colMax = new int[n];
        int[][] ans = new int[m][n];
        for (int[] num : nums) {
            int i = num[1], j = num[2];
            ans[i][j] = Math.max(rowMax[i], colMax[j]) + 1;
            rowMax[i] = ans[i][j];
            colMax[j] = ans[i][j];
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> minScore(vector<vector<int>>& grid) {
        vector<tuple<int, int, int>> nums;
        int m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                nums.push_back({grid[i][j], i, j});
            }
        }
        sort(nums.begin(), nums.end());
        vector<int> rowMax(m);
        vector<int> colMax(n);
        vector<vector<int>> ans(m, vector<int>(n));
        for (auto [_, i, j] : nums) {
            ans[i][j] = max(rowMax[i], colMax[j]) + 1;
            rowMax[i] = colMax[j] = ans[i][j];
        }
        return ans;
    }
};

Go

func minScore(grid [][]int) [][]int {
	m, n := len(grid), len(grid[0])
	nums := [][]int{}
	for i, row := range grid {
		for j, v := range row {
			nums = append(nums, []int{v, i, j})
		}
	}
	sort.Slice(nums, func(i, j int) bool { return nums[i][0] < nums[j][0] })
	rowMax := make([]int, m)
	colMax := make([]int, n)
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
	}
	for _, num := range nums {
		i, j := num[1], num[2]
		ans[i][j] = max(rowMax[i], colMax[j]) + 1
		rowMax[i] = ans[i][j]
		colMax[j] = ans[i][j]
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

TypeScript

function minScore(grid: number[][]): number[][] {
    const m = grid.length;
    const n = grid[0].length;
    const nums = [];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            nums.push([grid[i][j], i, j]);
        }
    }
    nums.sort((a, b) => a[0] - b[0]);
    const rowMax = new Array(m).fill(0);
    const colMax = new Array(n).fill(0);
    const ans = Array.from({ length: m }, _ => new Array(n));
    for (const [_, i, j] of nums) {
        ans[i][j] = Math.max(rowMax[i], colMax[j]) + 1;
        rowMax[i] = colMax[j] = ans[i][j];
    }
    return ans;
}

...