É um tipo de árvore binária, onde cada nó possui um valor associado e esse valor é quem define em que posição da árvore ele será inserido. Além disso, não possui elementos repetidos.
Para cada nó pai:
- Todos os valores da subárvore esquerda são menores que o nó pai!
- Todos os valores da subárvore direita são maiores que o nó pai!
Para inserir um valor na árvore deve-se seguir a receita:
- Compare o valor com a raiz.
- Se o valor é menor que a raiz então mande a subárvore da esquerda inserir o valor.
- Se o valor é maior que a raiz então mande a subárvore da direita inserir o valor.
OBS.: Existe o caso onde a inserção é feita na raiz (árvore vazia)
Fonte: Math Warehouse
Pseudocódigo
Complexidade:
Caso Médio: O(log n)
Pior Caso: O(n) (árvore não balanceada)
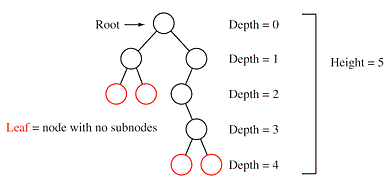
Informa a altura da árvore
Fonte: Include Help
Pseudocódigo
É necessário ter cuidado em 3 casos:
- Caso 1: Nó que irá ser removido é um nó folha
Simulação feita no Visualgo
- Caso 2: Nó que irá ser removido tem 1 filho
Simulação feita no Visualgo
- Caso 3: Nó que irá ser removido tem 2 filhos
Simulação feita no Visualgo
Pseudocódigo
Fonte: Wikipedia
Complexidade:
Caso Médio: O(log n)
Pior Caso: O(n) (árvore não balanceada)
O máximo da árvore é o elemento mais à direita e o mínimo é o mais à esquerda.
Fonte: Pantuza
Fonte: Pantuza
Sucessor: imagine que os elementos da árvore estão em um array ordenado, o sucessor de v é o próximo elemento no array, ou seja, se v está na posição i, o sucessor de v está na posição i + 1.
- Possui filho à direita.
- Caso contrário, o sucessor do nó será o ancestral mais baixo dele cujo filho da esquerda também seja um ancestral.
Predecessor: imagine novamente que os elementos da árvore estão em um array ordenado, o predecessor de v é o elemento anterior a ele no array, ou seja, se v está na posição i, o predecessor de v está na posição i - 1.
- Possui filho à esquerda.
- Caso contrário, o seu predecessor será o seu ancestral mais baixo cujo seu filho direito seja também um ancestral do nó.
OBS.: Se eu chamar o sucessor do máximo da árvore ou o predecessor do mínimo da árvore ambos os casos darão resultado
null.
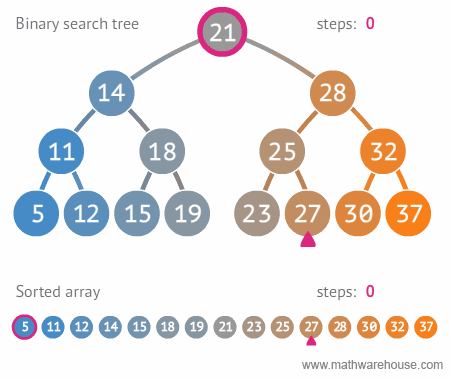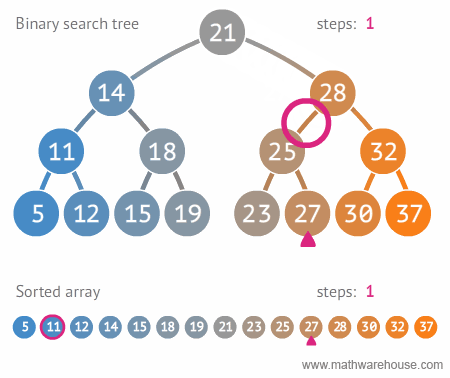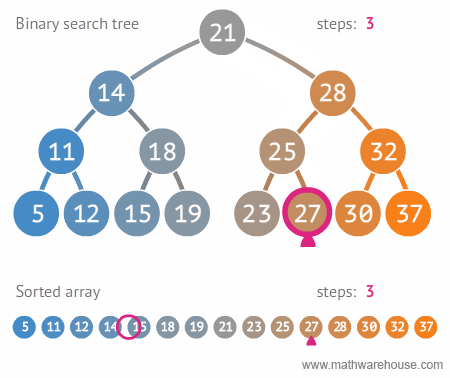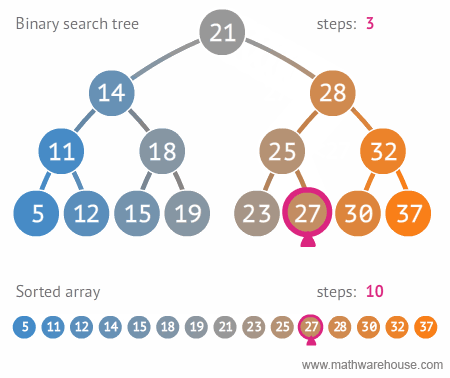
Para buscar um valor na árvore deve-se seguir a receita:
- Compare o valor com a raiz.
- Se o valor é menor que a raiz então mande a subárvore da esquerda buscar o valor.
- Se o valor é maior que a raiz então mande a subárvore da direita buscar o valor.
Fonte: Math Warehouse
Complexidade:
Caso Médio: O(log n)
Pior Caso: O(n) (árvore não balanceada)
- Pré-ordem
Coloca em um array todos os elementos da árvore seguindo o seguinte caminho: RAIZ, ESQUERDA e DIREITA.
- Pós-ordem
Coloca em um array todos os elementos da árvore seguindo o seguinte caminho: ESQUERDA, DIREITA e RAIZ.
- Ordem
Coloca num array todos os elementos da árvore seguindo o seguinte caminho: ESQUERDA, RAIZ e DIREITA.