3203. Find Minimum Diameter After Merging Two Trees

[mah-shamim]

Topics: Tree, Depth-First Search, Breadth-First Search, Graph

There exist two undirected trees with n and m nodes, numbered from 0 to n - 1 and from 0 to m - 1, respectively. You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the first tree and edges2[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the second tree.

You must connect one node from the first tree with another node from the second tree with an edge.

Return the minimum possible diameter of the resulting tree.

The diameter of a tree is the length of the longest path between any two nodes in the tree.

Example 1:

• Input: edges1 = [[0,1],[0,2],[0,3]], edges2 = [[0,1]]
• Output: 3
• Explanation: We can obtain a tree of diameter 3 by connecting node 0 from the first tree with any node from the second tree.

Example 2:

• Input: edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]], edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]
• Output: 5
• Explanation: We can obtain a tree of diameter 5 by connecting node 0 from the first tree with node 0 from the second tree.

Constraints:

• 1 <= n, m <= 105
• edges1.length == n - 1
• edges2.length == m - 1
• edges1[i].length == edges2[i].length == 2
• edges1[i] = [ai, bi]
• 0 <= ai, bi < n
• edges2[i] = [ui, vi]
• 0 <= ui, vi < m
• The input is generated such that edges1 and edges2 represent valid trees.

Hint:

1. Suppose that we connected node a in tree1 with node b in tree2. The diameter length of the resulting tree will be the largest of the following 3 values:
   1. The diameter of tree 1.
   2. The diameter of tree 2.
   3. The length of the longest path that starts at node a and that is completely within Tree 1 + The length of the longest path that starts at node b and that is completely within Tree 2 + 1.
      The added one in the third value is due to the additional edge that we have added between trees 1 and 2.
2. Values 1 and 2 are constant regardless of our choice of a and b. Therefore, we need to pick a and b in such a way that minimizes value 3.
3. If we pick a and b optimally, they will be in the diameters of Tree 1 and Tree 2, respectively. Exactly which nodes of the diameter should we pick?
4. a is the center of the diameter of tree 1, and b is the center of the diameter of tree 2.

[mah-shamim]

We need to approach it step-by-step with a focus on understanding how to calculate the diameter of a tree and how connecting the two trees influences the overall diameter.

Steps to solve:

1. Find the diameter of each tree:

   • The diameter of a tree is the longest path between any two nodes. To find it, we can use the following two-step process:
     1. Perform a BFS (or DFS) from an arbitrary node to find the farthest node (let's call this node A).
     2. Perform another BFS (or DFS) starting from A to find the farthest node from A (let's call this node B), and the distance from A to B will be the diameter of the tree.

2. Determine the optimal nodes to connect:

   • From the hint in the problem, the best way to minimize the additional diameter when connecting two trees is to connect the centers of the diameters of both trees. This will minimize the longest path caused by the new edge.
   • The optimal node in a tree's diameter is typically the "center", which can be found by performing a BFS from the endpoints of the diameter and finding the middle of the longest path.

3. Minimize the total diameter:

   • Once we find the centers of both trees, the new diameter is the maximum of:
     • The diameter of Tree 1.
     • The diameter of Tree 2.
     • The sum of the longest path within Tree 1, the longest path within Tree 2, and 1 for the new connecting edge.

Let's implement this solution in PHP: 3203. Find Minimum Diameter After Merging Two Trees

<?php
/**
 * @param Integer[][] $edges1
 * @param Integer[][] $edges2
 * @return Integer
 */
function minimumDiameterAfterMerge($edges1, $edges2) {
    // Construct adjacency list for Tree 1 and Tree 2
    $n = count($edges1) + 1;
    $m = count($edges2) + 1;

    $edgesTree1 = array_fill(0, $n, []);
    foreach ($edges1 as $edge) {
        list($a, $b) = $edge;
        $edgesTree1[$a][] = $b;
        $edgesTree1[$b][] = $a;
    }

    $edgesTree2 = array_fill(0, $m, []);
    foreach ($edges2 as $edge) {
        list($u, $v) = $edge;
        $edgesTree2[$u][] = $v;
        $edgesTree2[$v][] = $u;
    }

    // Find the diameter and center of both trees
    list($diameter1, $center1) = $this->getDiameterAndCenter($n, $edgesTree1);
    list($diameter2, $center2) = $this->getDiameterAndCenter($m, $edgesTree2);

    // Now find the longest paths in each tree from their respective centers
    list($distFromCenter1, $farthestFromCenter1) = $this->bfs($n, $edgesTree1, $center1);
    list($distFromCenter2, $farthestFromCenter2) = $this->bfs($m, $edgesTree2, $center2);

    // The result is the maximum of the 3 diameters
    return max($diameter1, $diameter2, $distFromCenter1[$farthestFromCenter1] + 1 + $distFromCenter2[$farthestFromCenter2]);
}

/**
 * Helper function to find the diameter of a tree and the farthest node from a start node
 *
 * @param $n
 * @param $edges
 * @param $start
 * @return array
 */
function bfs($n, $edges, $start) {
    $dist = array_fill(0, $n, -1);
    $dist[$start] = 0;
    $queue = [$start];
    $farthestNode = $start;

    while (count($queue) > 0) {
        $node = array_shift($queue);
        foreach ($edges[$node] as $neighbor) {
            if ($dist[$neighbor] == -1) {
                $dist[$neighbor] = $dist[$node] + 1;
                $queue[] = $neighbor;
                if ($dist[$neighbor] > $dist[$farthestNode]) {
                    $farthestNode = $neighbor;
                }
            }
        }
    }
    return [$dist, $farthestNode];
}

/**
 * Helper function to find the diameter of a tree and its center
 *
 * @param $n
 * @param $edges
 * @return array
 */
function getDiameterAndCenter($n, $edges) {
    // Find farthest node from an arbitrary node (node 0)
    list($distFromFirst, $farthestFromFirst) = $this->bfs($n, $edges, 0);

    // Find farthest node from the farthest node found (this gives the diameter's length)
    list($distFromFarthest, $farthestFromFarthest) = $this->bfs($n, $edges, $farthestFromFirst);

    // Now find the center (middle of the diameter)
    $path = [];
    $current = $farthestFromFarthest;
    while ($current != $farthestFromFirst) {
        $path[] = $current;
        foreach ($edges[$current] as $neighbor) {
            if ($distFromFarthest[$neighbor] == $distFromFarthest[$current] - 1) {
                $current = $neighbor;
                break;
            }
        }
    }
    $path[] = $farthestFromFirst;
    $diameterLength = $distFromFarthest[$farthestFromFarthest];
    $center = $path[floor(count($path) / 2)];

    return [$diameterLength, $center];
}

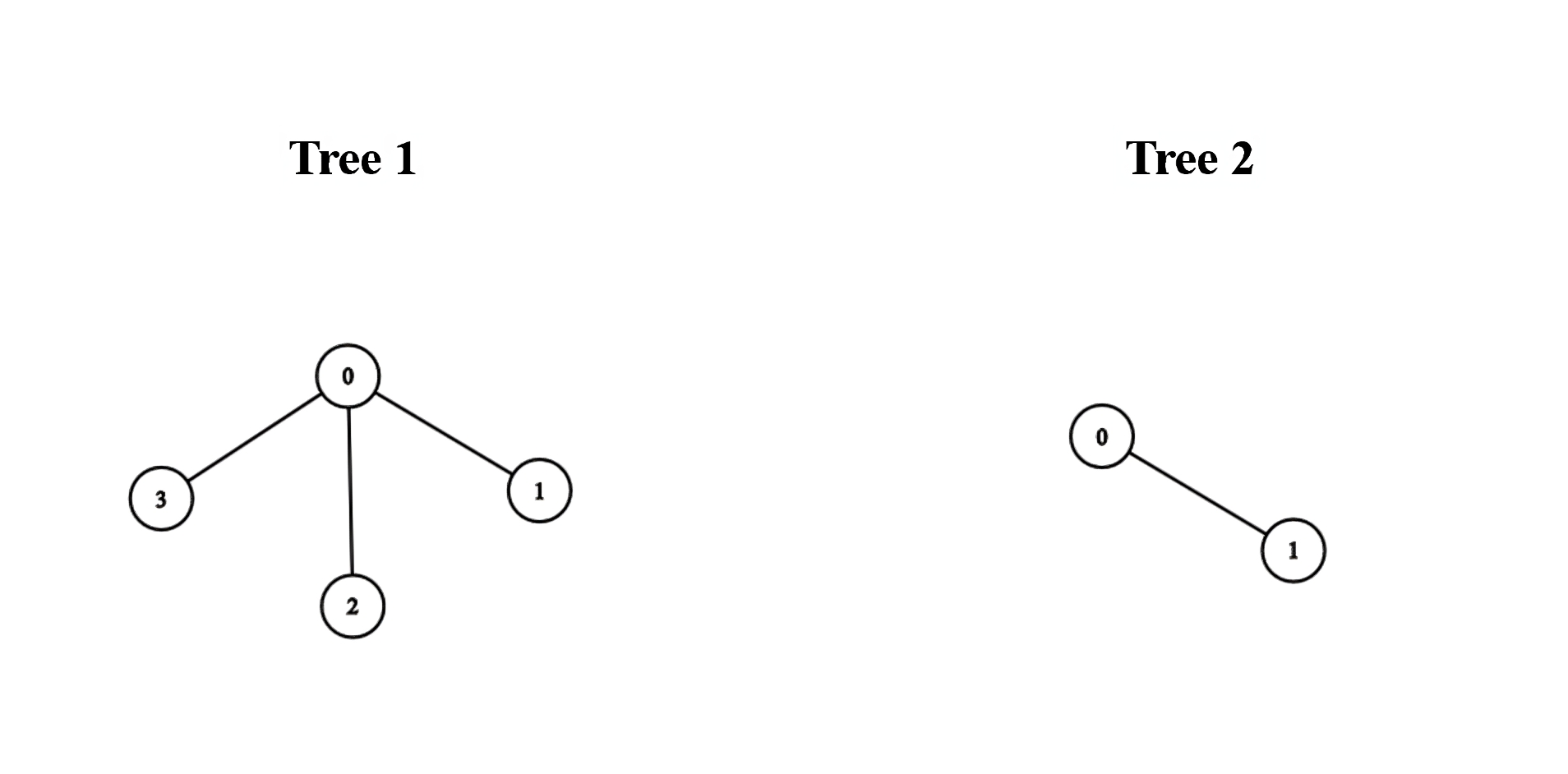
// Example 1
$edges1 = [[0,1],[0,2],[0,3]];
$edges2 = [[0,1]];
echo minimumDiameterAfterMerge($edges1, $edges2);  // Output: 3

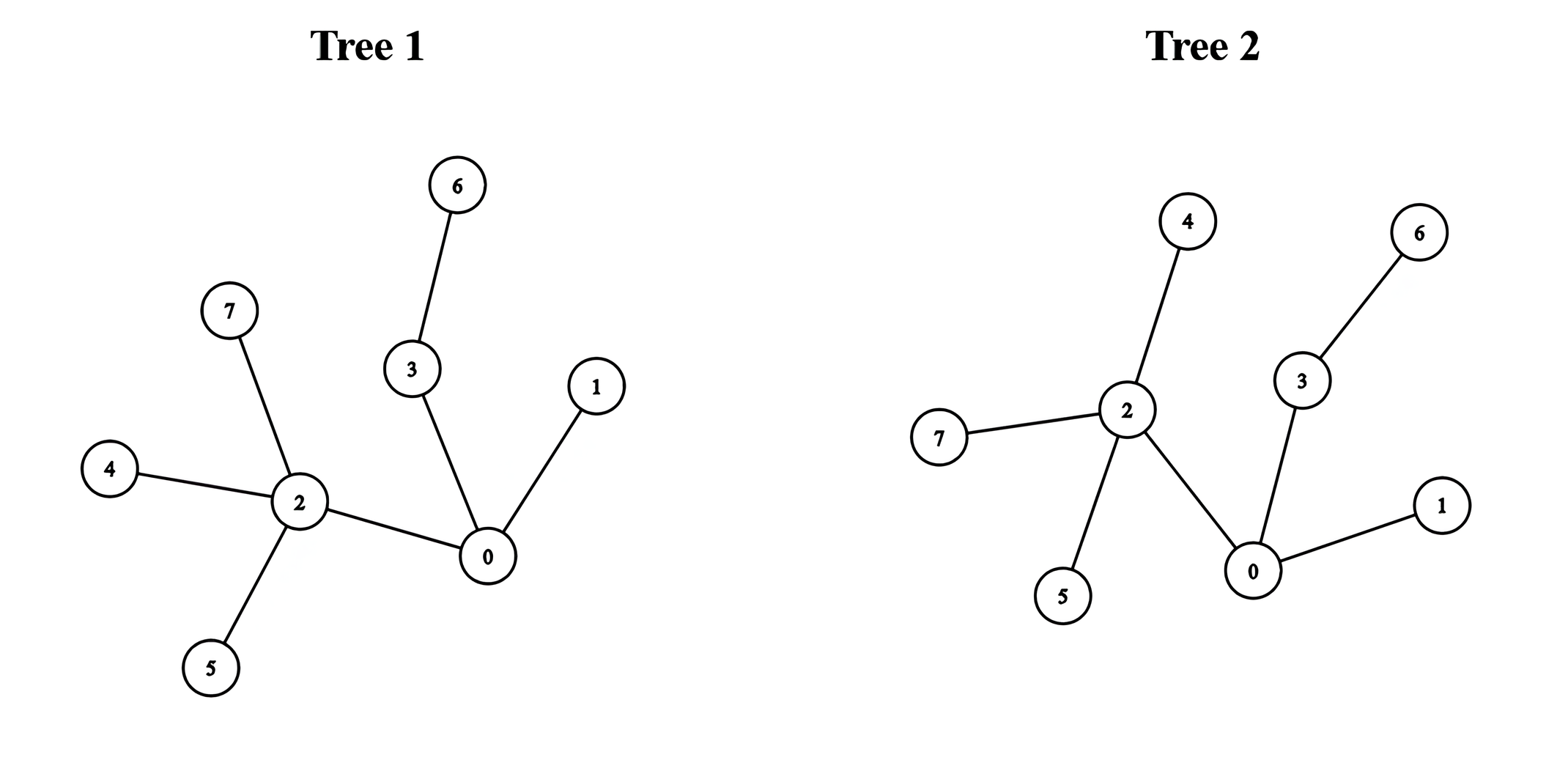
// Example 2
$edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]];
$edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]];
echo minimumDiameterAfterMerge($edges1, $edges2);  // Output: 5
?>

Explanation:

1. BFS Helper Function: The bfs function calculates the farthest node from a given starting node and returns the distance array and the farthest node found. This is essential for calculating the diameter of the tree.

2. Get Diameter and Center: The getDiameterAndCenter function finds the diameter of a tree and its center. The center of the tree is crucial for minimizing the new tree's diameter when merging two trees.

3. Main Solution:

   • We first build adjacency lists for both trees.
   • We calculate the diameter and center for both trees.
   • We perform BFS from the centers of both trees to get the longest paths within each tree.
   • Finally, we calculate the maximum of the three values to get the minimum diameter of the merged tree.

Time Complexity:

• Constructing the adjacency list: O(n + m)
• BFS traversal: O(n + m)
• Overall time complexity is O(n + m), which is efficient for the input size limit of 105.

This approach ensures we find the minimum possible diameter when merging the two trees.

[kovatz]

Thanks to solve this problem

[mah-shamim]

Thanks