2577. Minimum Time to Visit a Cell In a Grid

[mah-shamim]

Topics: Array, Breadth-First Search, Graph, Heap (Priority Queue), Matrix, Shortest Path

You are given a m x n matrix grid consisting of non-negative integers where grid[row][col] represents the minimum time required to be able to visit the cell (row, col), which means you can visit the cell (row, col) only when the time you visit it is greater than or equal to grid[row][col].

You are standing in the top-left cell of the matrix in the 0th second, and you must move to any adjacent cell in the four directions: up, down, left, and right. Each move you make takes 1 second.

Return the minimum time required in which you can visit the bottom-right cell of the matrix. If you cannot visit the bottom-right cell, then return -1.

Example 1:

• Input: grid = [[0,1,3,2],[5,1,2,5],[4,3,8,6]]
• Output: 7
• Explanation: One of the paths that we can take is the following:
  • at t = 0, we are on the cell (0,0).
  • at t = 1, we move to the cell (0,1). It is possible because grid[0][1] <= 1.
  • at t = 2, we move to the cell (1,1). It is possible because grid[1][1] <= 2.
  • at t = 3, we move to the cell (1,2). It is possible because grid[1][2] <= 3.
  • at t = 4, we move to the cell (1,1). It is possible because grid[1][1] <= 4.
  • at t = 5, we move to the cell (1,2). It is possible because grid[1][2] <= 5.
  • at t = 6, we move to the cell (1,3). It is possible because grid[1][3] <= 6.
  • at t = 7, we move to the cell (2,3). It is possible because grid[2][3] <= 7.
    The final time is 7. It can be shown that it is the minimum time possible.

Example 2:

• Input: grid = [[0,2,4],[3,2,1],[1,0,4]]
• Output: -1
• Explanation: There is no path from the top left to the bottom-right cell.

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 10>sup>5
• 0 <= grid[i][j] <= 10>sup>5
• grid[0][0] == 0

Hint:

1. Try using some algorithm that can find the shortest paths on a graph.
2. Consider the case where you have to go back and forth between two cells of the matrix to unlock some other cells.

[mah-shamim]

We can apply a modified version of Dijkstra's algorithm using a priority queue. This problem essentially asks us to find the shortest time required to visit the bottom-right cell from the top-left cell, where each move has a time constraint based on the values in the grid.

Approach:

1. Graph Representation: Treat each cell in the grid as a node. The edges are the adjacent cells (up, down, left, right) that you can move to.

2. Priority Queue (Min-Heap): Use a priority queue to always explore the cell with the least time required. This ensures that we are processing the cells in order of the earliest time we can reach them.

3. Modified BFS: For each cell, we will check if we can move to its neighboring cells and update the time at which we can visit them. If a cell is visited at a later time than the current, we add it back into the queue with the new time.

4. Early Exit: Once we reach the bottom-right cell, we can return the time. If we exhaust the queue without reaching it, return -1.

Let's implement this solution in PHP: 2577. Minimum Time to Visit a Cell In a Grid

<?php
/**
 * @param Integer[][] $grid
 * @return Integer
 */
function minimumTime($grid) {
    $m = count($grid);
    $n = count($grid[0]);

    // Early exit if the adjacent cells from the starting point are both blocked
    if ($grid[0][1] > 1 && $grid[1][0] > 1) {
        return -1;
    }

    // Directional movements: right, down, left, up
    $dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]];

    // Priority queue to store (time, row, col)
    $minHeap = new SplPriorityQueue();
    $minHeap->setExtractFlags(SplPriorityQueue::EXTR_DATA); // Extract data only
    $minHeap->insert([0, 0, 0], 0); // (time, i, j)

    // Seen array to track visited cells
    $seen = array_fill(0, $m, array_fill(0, $n, false));
    $seen[0][0] = true;

    while (!$minHeap->isEmpty()) {
        list($time, $i, $j) = $minHeap->extract();
        if ($i === $m - 1 && $j === $n - 1) {
            return $time; // Reached the bottom-right cell
        }

        foreach ($dirs as $dir) {
            $x = $i + $dir[0];
            $y = $j + $dir[1];

            // Skip invalid or already visited cells
            if ($x < 0 || $x >= $m || $y < 0 || $y >= $n || $seen[$x][$y]) {
                continue;
            }

            // Calculate the waiting time if needed
            $extraWait = ($grid[$x][$y] - $time) % 2 === 0 ? 1 : 0;
            $nextTime = max($time + 1, $grid[$x][$y] + $extraWait);

            $minHeap->insert([$nextTime, $x, $y], -$nextTime); // Use -$nextTime to mimic min-heap
            $seen[$x][$y] = true;
        }
    }

    return -1; // Unable to reach the bottom-right cell
}

// Example 1
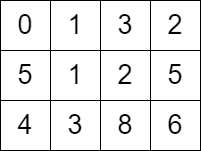
$grid1 = [
    [0, 1, 3, 2],
    [5, 1, 2, 5],
    [4, 3, 8, 6]
];
echo minimumTime($grid1) . PHP_EOL; // Output: 7

// Example 2
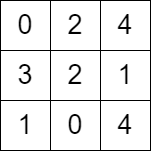
$grid2 = [
    [0, 2, 4],
    [3, 2, 1],
    [1, 0, 4]
];
echo minimumTime($grid2) . PHP_EOL; // Output: -1
?>

Explanation:

1. Priority Queue:
   The SplPriorityQueue is used to ensure that the cells with the minimum time are processed first. The priority is stored as -time because PHP's SplPriorityQueue is a max-heap by default.

2. Traversal:
   Starting from the top-left cell (0, 0), the algorithm processes all reachable cells, considering the earliest time each can be visited (max(0, grid[newRow][newCol] - (time + 1))).

3. Visited Cells:
   A visited array keeps track of cells that have already been processed to avoid redundant computations and infinite loops.

4. Boundary and Validity Check:
   The algorithm ensures we stay within the bounds of the grid and processes only valid neighbors.

5. Time Calculation:
   Each move takes one second, and if the cell requires waiting (i.e., grid[newRow][newCol] > time + 1), the algorithm waits until the required time.

6. Edge Case:
   If the queue is exhausted and the bottom-right cell is not reached, the function returns -1.

---

Complexity Analysis

1. Time Complexity:

   • Each cell is added to the priority queue at most once: O(m x n x log(m x n)), where m and n are the grid dimensions.

2. Space Complexity:

   • The space for the priority queue and the visited array is O(m x n).

---

Example Runs

Input:

$grid = [
    [0, 1, 3, 2],
    [5, 1, 2, 5],
    [4, 3, 8, 6]
];
echo minimumTime($grid); // Output: 7

Input:

$grid = [
    [0, 2, 4],
    [3, 2, 1],
    [1, 0, 4]
];
echo minimumTime($grid); // Output: -1

This solution is efficient and works well within the constraints.

[basharul-siddike]

Thanks to solve the "Minimum Time to Visit a Cell in a Grid" problem

[mah-shamim]

Thanks