2684. Maximum Number of Moves in a Grid #763
-
|
Topics: You are given a 0-indexed You can start at any cell in the first column of the matrix, and traverse the grid in the following way:
Return the maximum number of moves that you can perform. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We can use Dynamic Programming (DP) to keep track of the maximum number of moves from each cell, starting from any cell in the first column. Here’s the step-by-step approach: Approach:
Let's implement this solution in PHP: 2684. Maximum Number of Moves in a Grid <?php
/**
* @param Integer[][] $grid
* @return Integer
*/
function maxMoves($grid) {
$m = count($grid);
$n = count($grid[0]);
// Initialize DP array with 0 moves for all cells
$dp = array_fill(0, $m, array_fill(0, $n, 0));
// Traverse the grid from the second-to-last column to the first
for ($col = $n - 2; $col >= 0; $col--) {
for ($row = 0; $row < $m; $row++) {
// Possible moves (right-up, right, right-down)
$moves = [
[$row - 1, $col + 1],
[$row, $col + 1],
[$row + 1, $col + 1]
];
foreach ($moves as $move) {
list($newRow, $newCol) = $move;
if ($newRow >= 0 && $newRow < $m && $grid[$newRow][$newCol] > $grid[$row][$col]) {
$dp[$row][$col] = max($dp[$row][$col], $dp[$newRow][$newCol] + 1);
}
}
}
}
// Find the maximum moves starting from any cell in the first column
$maxMoves = 0;
for ($row = 0; $row < $m; $row++) {
$maxMoves = max($maxMoves, $dp[$row][0]);
}
return $maxMoves;
}
// Example usage:
$grid1 = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]];
$grid2 = [[3,2,4],[2,1,9],[1,1,7]];
echo maxMoves($grid1); // Output: 3
echo "\n";
echo maxMoves($grid2); // Output: 0
?>Explanation:
Complexity Analysis:
This solution is efficient given the constraints and will work within the provided limits. |
Beta Was this translation helpful? Give feedback.
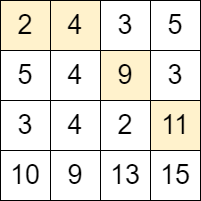
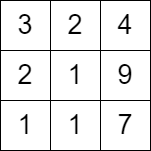
We can use Dynamic Programming (DP) to keep track of the maximum number of moves from each cell, starting from any cell in the first column. Here’s the step-by-step approach:
Approach:
Define DP Array: Let
dp[row][col]represent the maximum number of moves possible starting fromgrid[row][col]. Initialize this with0for all cells.Traverse the Grid:
col, calculate possible moves forcol-1.dp[row][col]based on possible moves(row - 1, col + 1),(row, col + 1), and(row + 1, col + 1), only if the value of the destination cell is strictly greater than the current cell.Calculate the Ma…