diff --git a/algorithms/002661-first-completely-painted-row-or-column/README.md b/algorithms/002661-first-completely-painted-row-or-column/README.md
new file mode 100644
index 000000000..f53f78f9f
--- /dev/null
+++ b/algorithms/002661-first-completely-painted-row-or-column/README.md
@@ -0,0 +1,138 @@
+2661\. First Completely Painted Row or Column
+
+**Difficulty:** Medium
+
+**Topics:** `Array`, `Hash Table`, `Matrix`
+
+You are given a **0-indexed** integer array `arr`, and an `m x n` integer **matrix** `mat`. `arr` and `mat` both contain **all** the integers in the range `[1, m * n]`.
+
+Go through each index `i` in `arr` starting from index `0` and paint the cell in `mat` containing the integer `arr[i]`.
+
+Return _the smallest index `i` at which either a row or a column will be completely painted in `mat`_.
+
+**Example 1:**
+
+![grid1](https://assets.leetcode.com/uploads/2023/01/18/grid1.jpg)
+
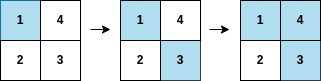
+- **Input:** arr = [1,3,4,2], mat = [[1,4],[2,3]]
+- **Output:** 2
+- **Explanation:** The moves are shown in order, and both the first row and second column of the matrix become fully painted at `arr[2]`.
+
+**Example 2:**
+
+![grid2](https://assets.leetcode.com/uploads/2023/01/18/grid2.jpg)
+
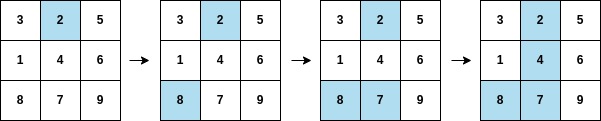
+- **Input:** arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
+- **Output:** 3
+- **Explanation:** The second column becomes fully painted at `arr[3]`.
+
+
+
+**Constraints:**
+
+- `m == mat.length`
+- `n = mat[i].length`
+- `arr.length == m * n`
+- <code>1 <= m, n <= 10<sup>5</sup></code>
+- <code>1 <= m * n <= 10<sup>5</sup></code>
+- `1 <= arr[i], mat[r][c] <= m * n`
+- All the integers of `arr` are **unique**.
+- All the integers of `mat` are **unique**.
+
+
+**Hint:**
+1. Can we use a frequency array?
+2. Pre-process the positions of the values in the matrix.
+3. Traverse the array and increment the corresponding row and column frequency using the pre-processed positions.
+4. If the row frequency becomes equal to the number of columns, or vice-versa return the current index.
+
+
+
+**Solution:**
+
+We can follow these steps:
+
+### Approach
+
+1. **Pre-process the positions of elements**:
+   - First, we need to store the positions of the elements in the matrix. We can create a dictionary (`position_map`) that maps each value in the matrix to its `(row, col)` position.
+
+2. **Frequency Arrays**:
+   - We need two frequency arrays: one for the rows and one for the columns.
+   - As we go through the `arr` array, we will increment the frequency of the respective row and column for each element.
+
+3. **Check for Complete Row or Column**:
+   - After each increment, check if any row or column becomes completely painted (i.e., its frequency reaches the size of the matrix's columns or rows).
+   - If so, return the current index.
+
+4. **Return the result**:
+   - The index where either a row or column is fully painted is our answer.
+
+### Detailed Steps
+1. Create a map `position_map` for each value in `mat` to its `(row, col)` position.
+2. Create arrays `row_count` and `col_count` to track the number of painted cells in each row and column.
+3. Traverse through `arr` and for each element, update the respective row and column counts.
+4. If at any point a row or column is completely painted, return that index.
+
+Let's implement this solution in PHP: **[2661. First Completely Painted Row or Column](https://github.com/mah-shamim/leet-code-in-php/tree/main/algorithms/002661-first-completely-painted-row-or-column/solution.php)**
+
+```php
+<?php
+/**
+ * @param Integer[] $arr
+ * @param Integer[][] $mat
+ * @return Integer
+ */
+function firstCompleteIndex($arr, $mat) {
+    ...
+    ...
+    ...
+    /**
+     * go to ./solution.php
+     */
+}
+
+// Example usage:
+$arr = [1, 3, 4, 2];
+$mat = [[1, 4], [2, 3]];
+echo firstCompleteIndex($arr, $mat); // Output: 2
+
+$arr = [2, 8, 7, 4, 1, 3, 5, 6, 9];
+$mat = [[3, 2, 5], [1, 4, 6], [8, 7, 9]];
+echo firstCompleteIndex($arr, $mat); // Output: 3
+?>
+```
+
+### Explanation:
+
+1. **Pre-processing positions**:
+   - We build a dictionary `position_map` where each value in `mat` is mapped to its `(row, col)` position. This helps in directly accessing the position of any value in constant time during the traversal of `arr`.
+
+2. **Frequency counts**:
+   - We initialize `row_count` and `col_count` arrays with zeros. These arrays will keep track of how many times a cell in a specific row or column has been painted.
+
+3. **Traversing the array**:
+   - For each value in `arr`, we look up its position in `position_map`, then increment the corresponding row and column counts.
+   - After updating the counts, we check if any row or column has reached its full size (i.e., `row_count[$row] == n` or `col_count[$col] == m`). If so, we return the current index `i`.
+
+4. **Return Result**:
+   - The first index where either a row or column is completely painted is returned.
+
+### Time Complexity:
+- **Pre-processing**: We build `position_map` in `O(m * n)`.
+- **Traversal**: We process each element of `arr` (which has a length of `m * n`), and for each element, we perform constant-time operations to update and check the row and column frequencies, which takes `O(1)` time.
+- Overall, the time complexity is `O(m * n)`.
+
+### Space Complexity:
+- We store the positions of all elements in `position_map`, and we use `O(m + n)` space for the frequency arrays. Therefore, the space complexity is `O(m * n)`.
+
+This solution should efficiently handle the problem within the given constraints.
+
+**Contact Links**
+
+If you found this series helpful, please consider giving the **[repository](https://github.com/mah-shamim/leet-code-in-php)** a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!
+
+If you want more helpful content like this, feel free to follow me:
+
+- **[LinkedIn](https://www.linkedin.com/in/arifulhaque/)**
+- **[GitHub](https://github.com/mah-shamim)**
\ No newline at end of file
diff --git a/algorithms/002661-first-completely-painted-row-or-column/solution.php b/algorithms/002661-first-completely-painted-row-or-column/solution.php
new file mode 100644
index 000000000..0da88fbb0
--- /dev/null
+++ b/algorithms/002661-first-completely-painted-row-or-column/solution.php
@@ -0,0 +1,43 @@
+<?php
+
+class Solution {
+
+    /**
+     * @param Integer[] $arr
+     * @param Integer[][] $mat
+     * @return Integer
+     */
+    function firstCompleteIndex($arr, $mat) {
+        $m = count($mat);
+        $n = count($mat[0]);
+
+        // Step 1: Preprocess the positions of elements in the matrix
+        $position_map = [];
+        for ($i = 0; $i < $m; $i++) {
+            for ($j = 0; $j < $n; $j++) {
+                $position_map[$mat[$i][$j]] = [$i, $j];
+            }
+        }
+
+        // Step 2: Initialize row and column counts
+        $row_count = array_fill(0, $m, 0); // Frequency of painted cells in each row
+        $col_count = array_fill(0, $n, 0); // Frequency of painted cells in each column
+
+        // Step 3: Traverse arr and update counts
+        foreach ($arr as $i => $value) {
+            list($row, $col) = $position_map[$value];
+
+            // Increment the row and column counts
+            $row_count[$row]++;
+            $col_count[$col]++;
+
+            // Step 4: Check if any row or column is fully painted
+            if ($row_count[$row] == $n || $col_count[$col] == $m) {
+                return $i;
+            }
+        }
+
+        // If no row or column is fully painted, return -1 (although the problem guarantees a solution)
+        return -1;
+    }
+}
\ No newline at end of file