README.rst

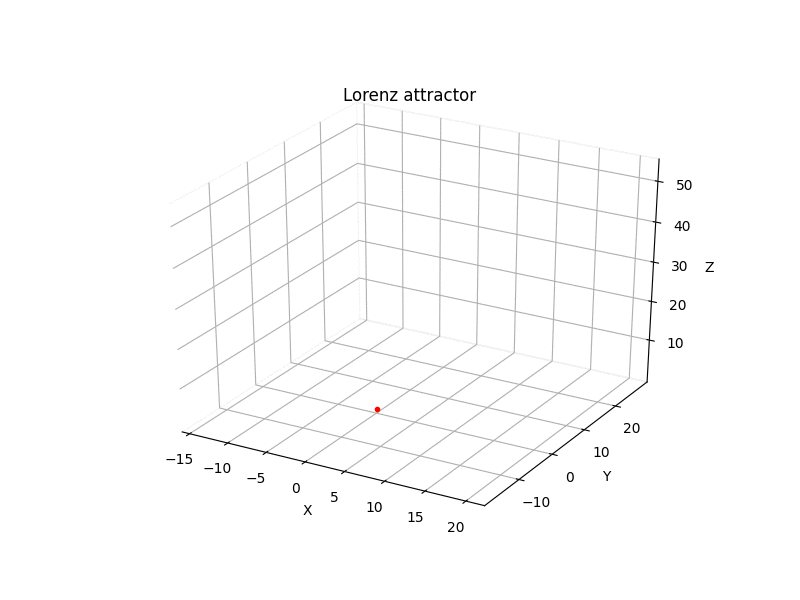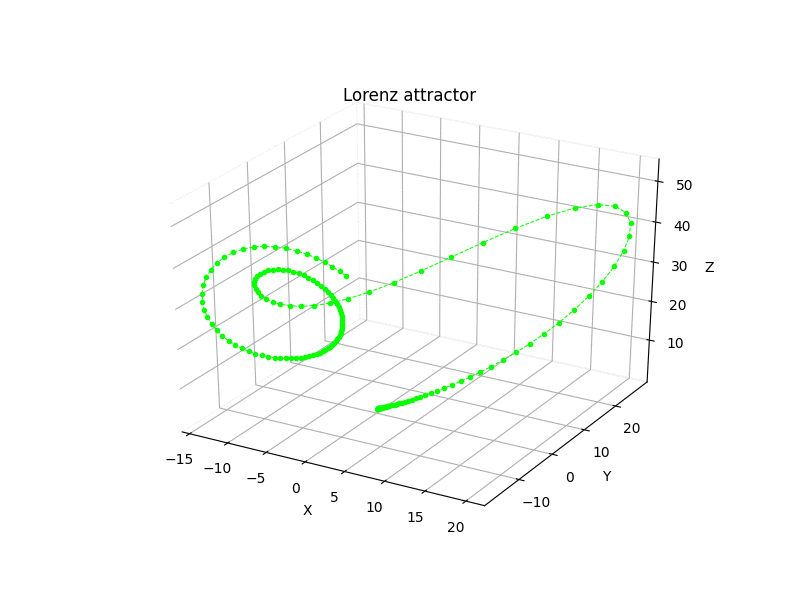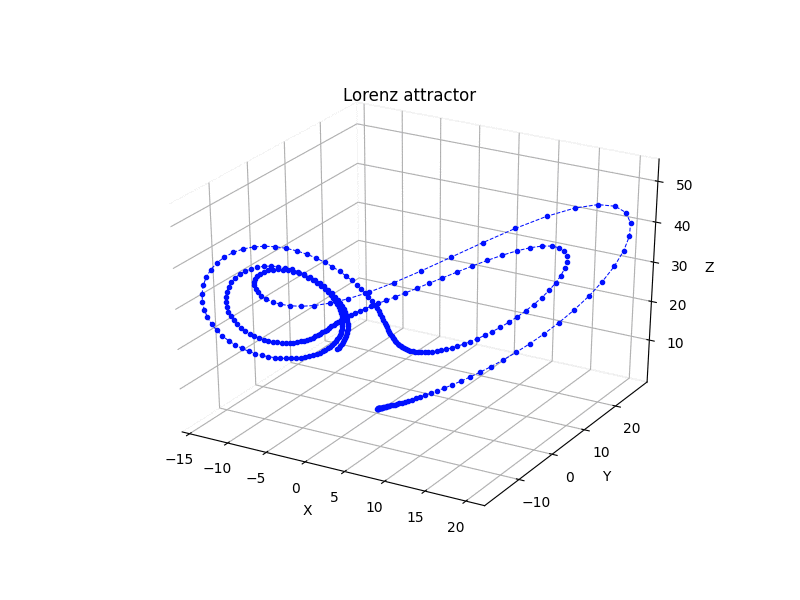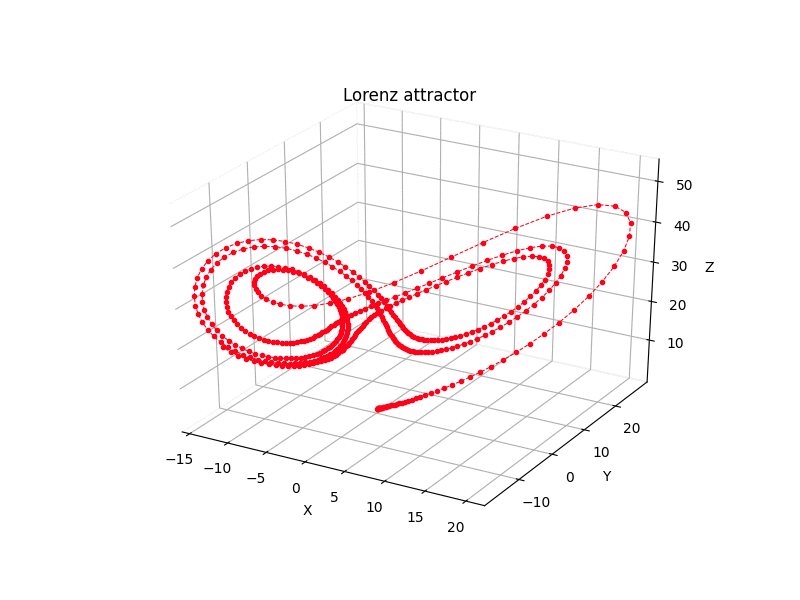
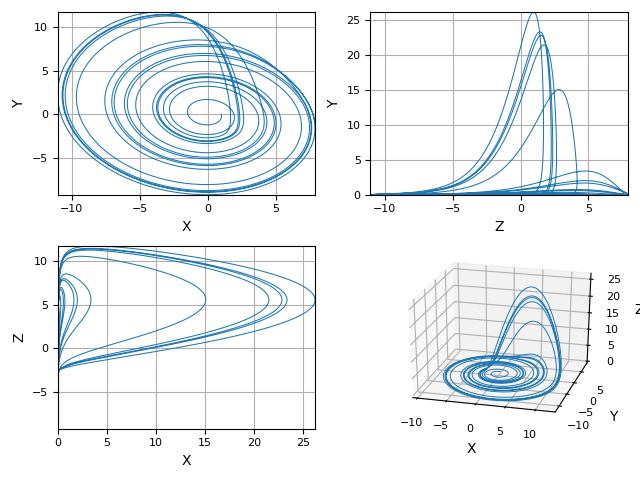
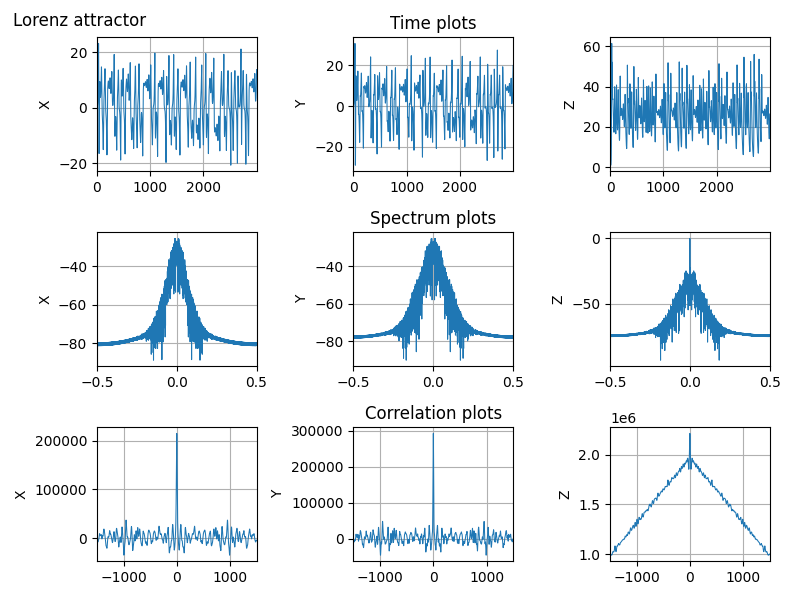
Python scripts for some 3rd-order chaotic systems (Lorenz attractor, Nose-Hoover oscillator, Rossler attractor, Riktake model, Duffing map etc.)

Chaotic attractors

Math model:

dx/dt = sigma * (y - x)
dy/dt = rho * x - y - x * z
dz/dt = x * y - beta * z

where sigma = 10, rho = 28 and beta = 8/3.

Main info

Title	Analysis and modeling chaotic systems
Author	Alexander Kapitanov
Contact	<email_hidden>
Project lang	Python 3
First Release	30 May 2019
License	GNU GPL 3.0.

Chaotic system

Rossler attractor:

dx/dt = -(y + z)
dy/dt = x + a * y
dz/dt = b + z * (x - c)

where a = 0.2, b = 0.2 and c = 5.7.

Spectrum and auto correlation

Source code

You can check the latest sources with the command:

$ git clone <chaospy.git>
$ cd chaospy
$ <install miniconda for your operation system>
$ conda create -y -n venv python==3.9
$ conda activate venv
$ pip install -r requirements.txt

Example run:

$ python run.py --show_plots --show_all lorenz

Dependencies

Project requirements: requirements.txt

Chaotic models

• Lorenz
• Rossler
• Rikitake
• Duffing
• Nose-Hoover
• Lotka-Volterra
• Wang
• Chua

Help

usage: parser.py [-h] [-p POINTS] [-s STEP]
                 [--init_point INIT_POINT [INIT_POINT ...]] [--show_plots]
                 [--save_plots] [--add_2d_gif]
                 {lorenz,rossler,rikitake,chua,duffing,wang,nose-hoover,lotka-volterra}
                 ...

    Specify command line arguments for dynamic system.Calculate some math
    parameters and plot some graphs of a given chaotic system.

    optional arguments:
      -h, --help            show this help message and exit
      -p POINTS, --points POINTS
                            Number of points for dymanic system. Default: 1024.
      -s STEP, --step STEP  Step size for calculating the next coordinates of
                            chaotic system. Default: 100.
      --init_point INIT_POINT [INIT_POINT ...]
                            Initial point as string of three floats: "X, Y, Z".
      --show_plots          Show plots of a model. Default: False.
      --save_plots          Save plots to PNG files. Default: False.
      --add_2d_gif          Add 2D coordinates to 3D model into GIF. Default:
                            False.

    Chaotic models:
      You can select one of the chaotic models:

      {lorenz,rossler,rikitake,chua,duffing,wang,nose-hoover,lotka-volterra}
        lorenz              Lorenz chaotic model
        rossler             Rossler chaotic model
        rikitake            Rikitake chaotic model
        chua                Chua chaotic model
        duffing             Duffing chaotic model
        wang                Wang chaotic model
        nose-hoover         Nose-hoover chaotic model
        lotka-volterra      Lotka-volterra chaotic model

Chaotic attractors are used as subparse command. Example:

Lorenz attractor

usage: parser.py lorenz [-h] [--sigma SIGMA] [--beta BETA] [--rho RHO]

optional arguments:
  -h, --help     show this help message and exit

Lorenz model arguments:
  --sigma SIGMA  Lorenz system parameter. Default: 10
  --beta BETA    Lorenz system parameter. Default: 2.6666
  --rho RHO      Lorenz system parameter. Default: 28

Chua circuit

usage: parser.py chua [-h] [--alpha ALPHA] [--beta BETA] [--mu0 MU0]
                      [--mu1 MU1]

optional arguments:
  -h, --help     show this help message and exit

Chua model arguments:
  --alpha ALPHA  Chua system parameter. Default: 0.1
  --beta BETA    Chua system parameter. Default: 28
  --mu0 MU0      Chua system parameter. Default: -1.143
  --mu1 MU1      Chua system parameter. Default: -0.714

See Also

• Wiki
• Habr