公式渲染有问题,详细报告可见博客https://www.xilluillblog.cn/2024/03/31/FFT%E5%8A%A0%E9%80%9F%E5%8D%B7%E7%A7%AF/
卷积在当前的图像处理领域中被广泛应用,是许多计算机视觉和图像处理任务的基础操作之一。然而,传统的时域卷积在处理大尺寸核(kernel)时可能效率较低。为了优化计算速度,傅里叶变换被引入到卷积中,通过将卷积操作转换到频域进行计算。本文旨在讨论卷积在图像处理中的重要性,并比较不同实现方式的性能,包括OpenCV和SciPy自带的卷积函数。最重要的是,本文编写了基于NumPy的频域加速卷积算法,比较了其与时域卷积的时间复杂度。
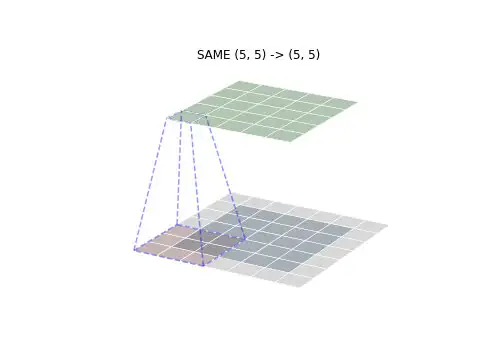
在图像处理领域,卷积是一种重要的操作,通过将图像与特定的核(kernel)进行卷积操作,可以实现一系列图像处理任务,如模糊、边缘检测、锐化等。卷积操作可以使图像在不同尺度上进行平滑或突出边缘等特征,从而帮助人们更好地理解图像中的信息。例如,通过应用不同的卷积核,可以检测图像中的边缘,提取纹理信息,或者进行图像去噪等处理,从而为后续的分析和识别提供更好的基础。
随着深度学习的发展,卷积神经网络(Convolutional Neural Networks,CNNs)成为图像处理和计算机视觉领域的重要工具。$CNNs$通过卷积层对图像进行特征提取,然后通过池化层和全连接层进行分类或回归等任务。卷积层的引入使得网络能够自动学习图像中的特征,从而在图像识别、分割、检测等任务中取得了巨大成功。
通过传统图像处理和深度学习两个角度介绍,可以更全面地展示卷积在图像处理中的重要性和意义。
在实现基于傅里叶变换的频域加速卷积算法时,考虑了使用其他语言的实现方式,包括C++和MATLAB。这两种语言在性能方面都有一定优势,C++具有较高的性能,而MATLAB能够充分利用硬件进行矩阵加速,从而提高计算效率。
然而,最终选择了使用Python和NumPy进行实现。NumPy是Python中用于科学计算的重要库,其底层实现部分采用C语言编写,具有较高的性能。NumPy提供了丰富的数学函数和数据结构,能够高效地进行数组操作和线性代数运算,使得基于NumPy的算法在性能上能够接近*C++*的实现。
选择Python作为实现平台还有其他几个重要原因。首先,Python作为一种高级语言,具有简洁易读的语法,使得算法的编写和调试更为方便。其次,Python平台提供了丰富的第三方库支持,例如OpenCV,可以方便地进行图像处理相关的比较和验证。最重要的是,Python作为一种流行的科学计算语言,拥有庞大的社区和生态系统,例如SciPy提供了一个卷积接口,以选择使用FFT加速或者直接进行卷积。
因此,尽管Python受限于一些性质导致了编写的底层算法性能不佳,但考虑到NumPy和Python平台的诸多优势,选择了Python和NumPy作为实现基于傅里叶变换的频域加速卷积算法的平台。
在OpenCV的文档中可以找到 **cv2.filter2D()**的原理。这个函数其实是计算的相关运算。这个情况很常见,无论是深度学习里面的可学习参量,还是说这次实验用的是对称卷积核。所以这个相关运算不会干扰本文的实验。
二维傅里叶变换其实是相当复杂的,关于他的快速实现有多种方法。但是不变的是其时间复杂度降至$O(nlogn)$,这为加速卷积运算提供了可能。
根据官方文档API可以看得到该函数的接收变量。
| 参数 | 类型 | 默认值 | 具体含义 |
|---|---|---|---|
| src | NumPy.ndarray | / | 原图像 |
| ddepth | int | / | 目标图像深度 |
| kernel | NumPy.ndarray | / | 卷积核 |
| anchor | tuple | (-1,-1) | 卷积锚点 |
| delta | / | 0 | 偏移量 |
| borderType | enum | cv2.BORDER_DEFALUT | 边缘类型 |
并且OpenCV本身用C++实现该函数时,当卷积核大小比较小时用时域卷积,而很大时用DFT加速运算。而本文则使用FFT加速运算。
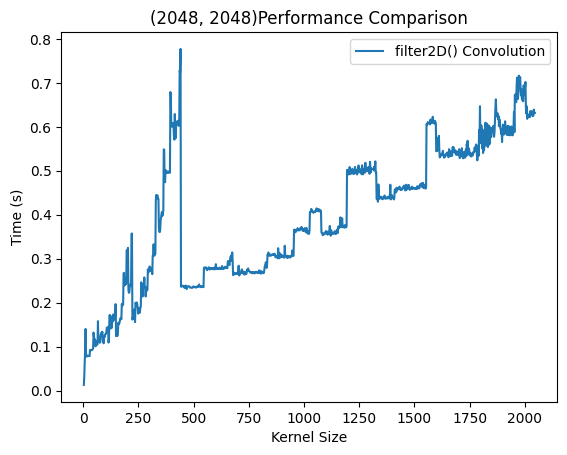
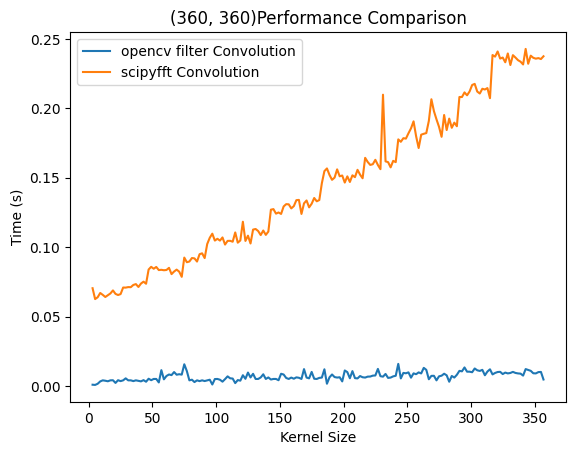
在图像尺寸为$2048×2048$下进行多次卷积调用该函数,可以测出该函数的性能曲线。蓝色曲线可以看出在相对尺寸较小的卷积核是近似$O(n^2)$快速增长的,而达到一定大小之后使用DFT加速了运算。可以看出相近尺寸的卷积核时间用时基本一致,这是因为进行DFT时的长宽选择固定,最后呈现出阶段性上升和整体的$O(n^2)$增长。
实际上无论是NumPy还是OpenCV都没有真正的时域卷积。因此我通过编写代码实现了一个多通道的时域卷积。
def conv2d_numpy(input_data, kernel, stride=1, padding=0):
# 获取输入数据的尺寸和通道数
# 如果输入数据是三通道的图像,那么获取通道数
dim= len(input_data.shape)
kernel = np.expand_dims(kernel, 2).repeat(dim, axis=2)
if dim == 2:
input_data = np.expand_dims(input_data, 2).repeat(1, axis=2)
input_height, input_width, input_channels = input_data.shape
# 获取卷积核的尺寸和通道数
kernel_height, kernel_width,kernel_channels = kernel.shape
# 计算输出图像的尺寸
output_height = (input_height - kernel_height + 2 * padding) // stride + 1
output_width = (input_width - kernel_width + 2 * padding) // stride + 1
# 初始化输出图像
output_data = np.zeros((output_height, output_width,input_channels))
kernel_side = kernel_height//2
# 填充输入数据(根据填充数量添加额外的行和列)
if padding > 0:
input_data = np.pad(input_data, ((padding, padding), (padding, padding),(0,0)), mode='constant',constant_values = (0,0))
# 执行多通道卷积操作
for i in range(0, output_height, stride):
for j in range(0, output_width, stride):
for k in range(input_channels):
output_data[i // stride, j // stride,k] = np.sum(input_data[i:i+kernel_width, j:j+kernel_width, k] * kernel[:, :, k])
return output_data 虽然NumPy本身是C++实现具有高性能,但是python的循环速度非常慢,导致该算法性能极低。
根据公式可以推导出频域相乘可以代替时域卷积。但是值得注意的是,在离散信号中,频域相乘对应的是时域循环卷积,这同样适用于二维图像。
$$
\begin{aligned}
\text{y[n]}& =x[n]®h[n]=\sum_{m=0}^{N-1}x[m]h[((n-m))N],\quad n=0,1,\cdots,N-1\text{。} \
Y(k)& =\operatorname{DFT}{y[n]} \
&=\sum{k=0}^{N-1}\sum_{m=0}^{N-1}x[m]h[((n-m))N]\mathrm{e}^{-\mathrm{j}\frac{2\pi}Nkn} \
\text{}& =\sum{m=0}^{N-1}x[m]\sum_{k=0}^{N-1}h[((n-m))N]\mathrm{e}^{-\text{j}\frac{2\pi}Nkn} \
{}\text{}& =\sum{m=0}^{N-1}x[m]\mathrm{e}^{-\mathrm{j}\frac{2\pi}Nkm}\sum_{k=0}^{N-1}h[n]\mathrm{e}^{-\mathrm{j}\frac{2\pi}Nkn} \
&=X[k]H[k]
\end{aligned}
$$
测试算法时做的实验均为灰度图计算,后续实验将在三通道RGB彩色图上进行实验。
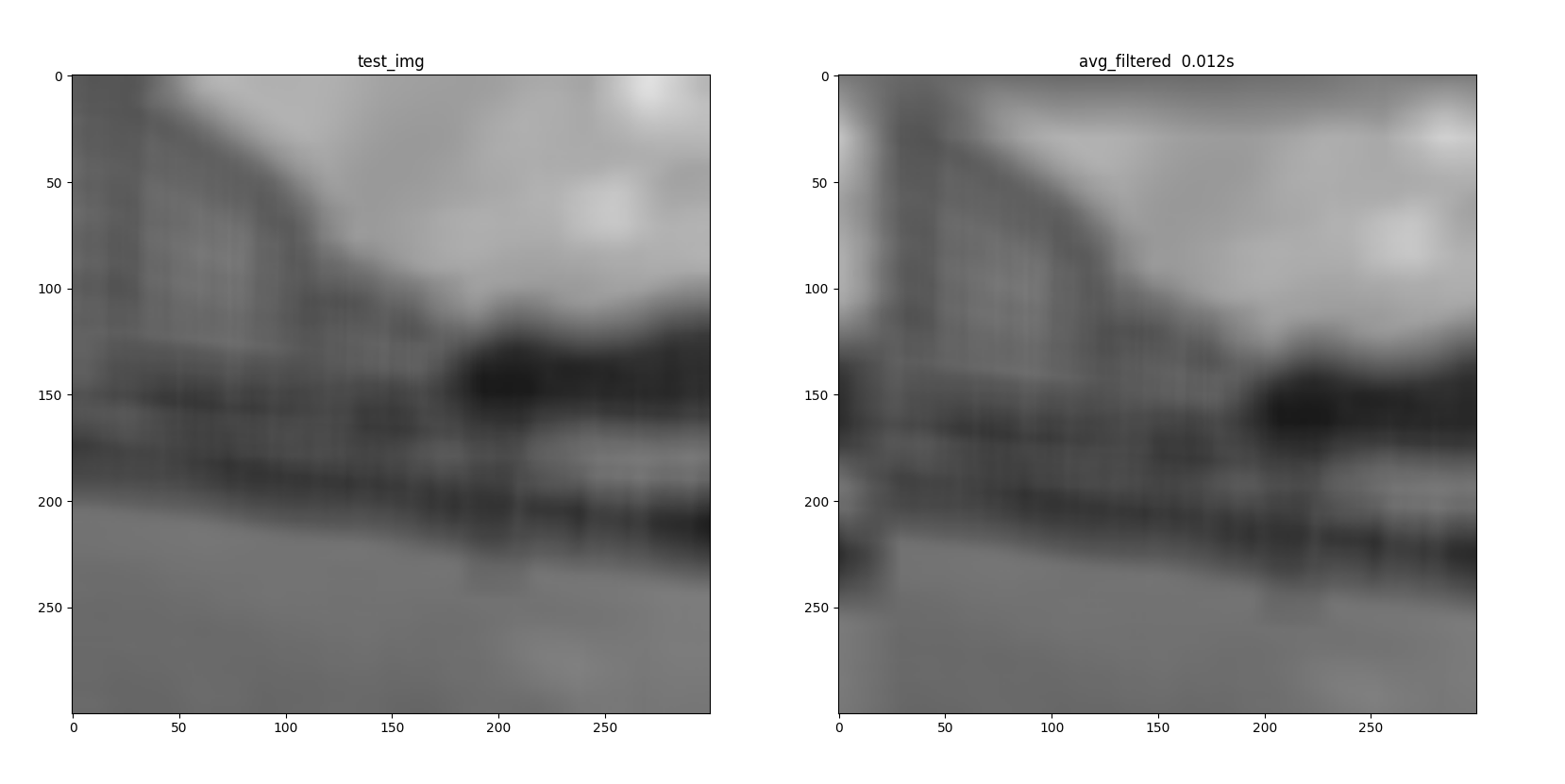
可以观察右侧结果图的边缘非常奇怪,这其实就是时域上的循环卷积,使图像整体进行了循环。所以需要格外的填充操作修复这一问题。
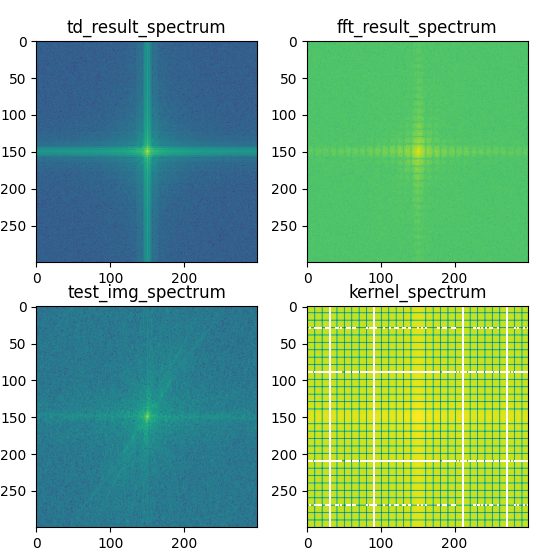
从频域也可以看出,直接相乘导致的方形分界线非常明显,而真正的时域卷积会略有不同。
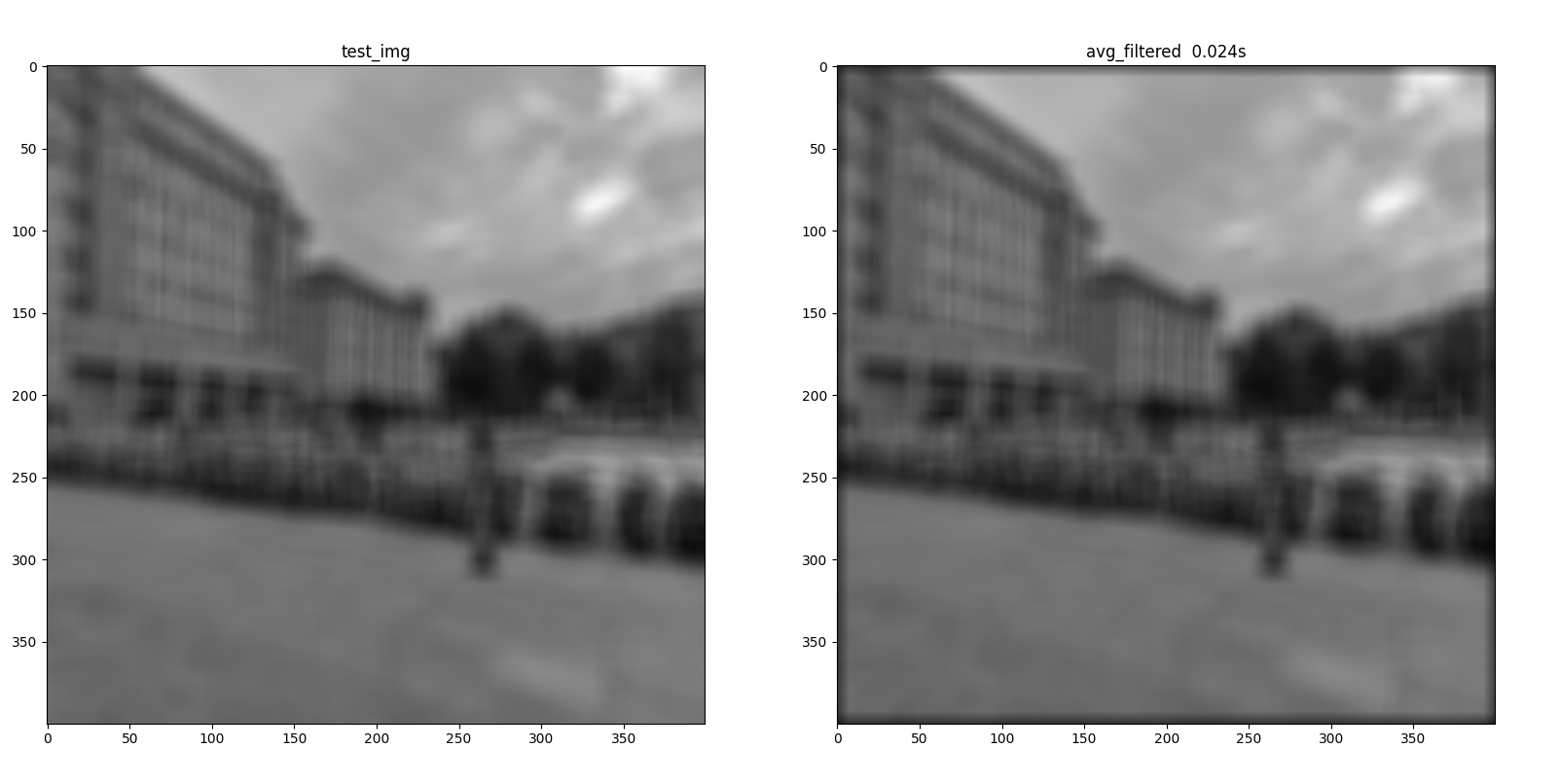
加入填充和裁剪操作才能让频域相乘逆变换这一操作正确执行,右图为镜像填充对比左图的常量填充。
SciPy其实提供了一个卷积接口,并且均为NumPy实现,性能比起自己手写的更加高效和稳定,因此本文也将这一接口加入了实验。
| 参数* | 类型 | 默认值 | 具体含义 |
|---|---|---|---|
| in1 | NumPy.ndarray | / | 原图像 |
| in2 | NumPy.ndarray | / | 卷积核 |
| mode | str {'full', 'valid', 'same'} | full | 输出尺寸 |
| method | str {'auto', 'direct', 'FFT'} | auto | 是否使用FFT加速 |
本文设计了filter2D方法和FFT方法对比,以及时域方法于FFT方法对比。前者在正常$2048×2048$尺寸下运行,后者在$360×360$分辨率下进行计算,确保在短时间内获得更多实验数据。同时在SciPy统一平台上做了相同的测试。
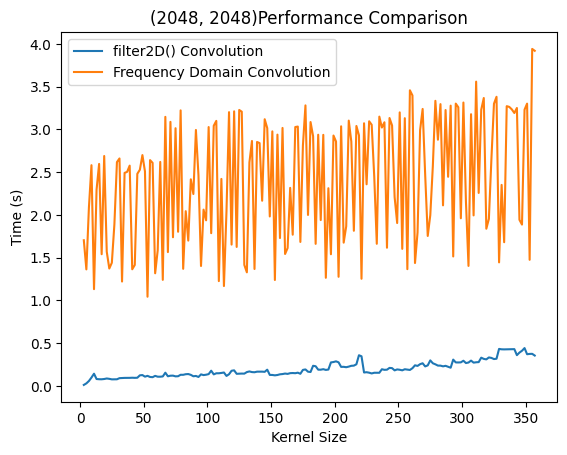
可以看出频域相乘这套算法会存在周期性或者随机性负载增加,推测应该是不同大小的卷积核在固定尺寸下进行FFT计算会花费不同的时间。整体也是缓慢上升趋势。而前半段使用时域卷积,后半段使用DFT加速的*filter2D()*方法则呈现出稳定上升趋势。
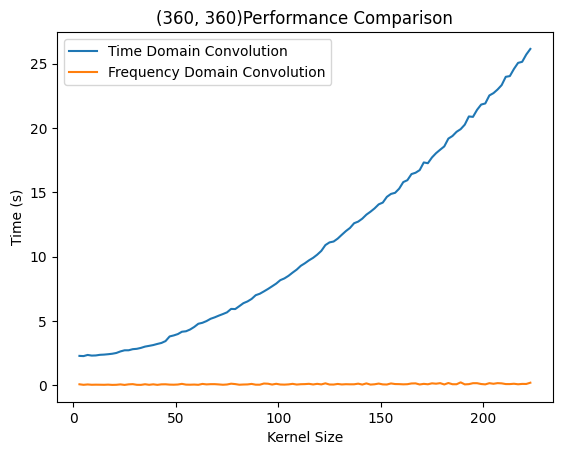
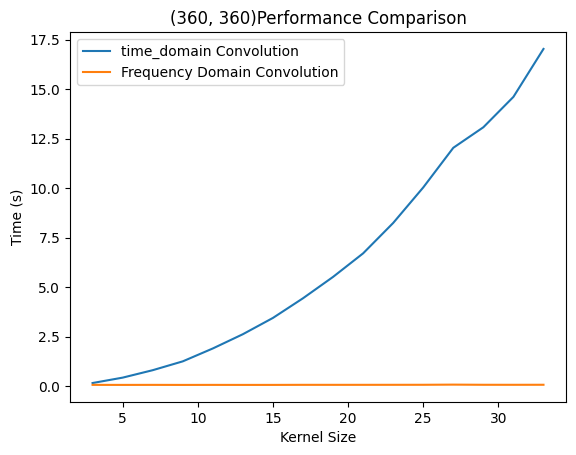
而时域卷积呈现出明显的$O(n^2)$复杂度,符合理论推测。当然,这一方法显著慢于前两种方法的原因在于python作为解释性语言在密集计算场景下性能不佳。而OpenCV是*C++编写的库,因此当有更多的计算交给C++*完成,就会获得更高的性能。这两次实验只能比较出几种算法的复杂度区别,而想看到两种方法在某一卷积核大小附近完成了性能反超,则需要更为统一的计算平台。
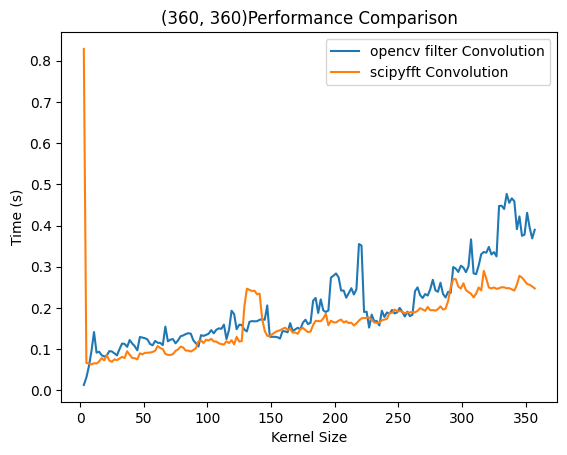
右侧为SciPy则提供了统一的性能比较平台,在上述实验条件下分别调用计算性能。用不同实验平台得出了相似结果,即时域卷积在很小的时候和FFT速度相当,在大尺寸下远慢于FFT方法。有意思的是,SciPy的时域实现还没有自己编写的快。
由于几种方法性能差异都太大,无法观察到FFT方法的时间复杂度,因此本文设计了SciPy和OpenCV的比较实验,其中图8右侧中OpenCV运行在2048×2048的方法下,由于已知OpenCV为$O(n^2)$复杂度,故通过这种方法比较得出FFT方法的复杂度。
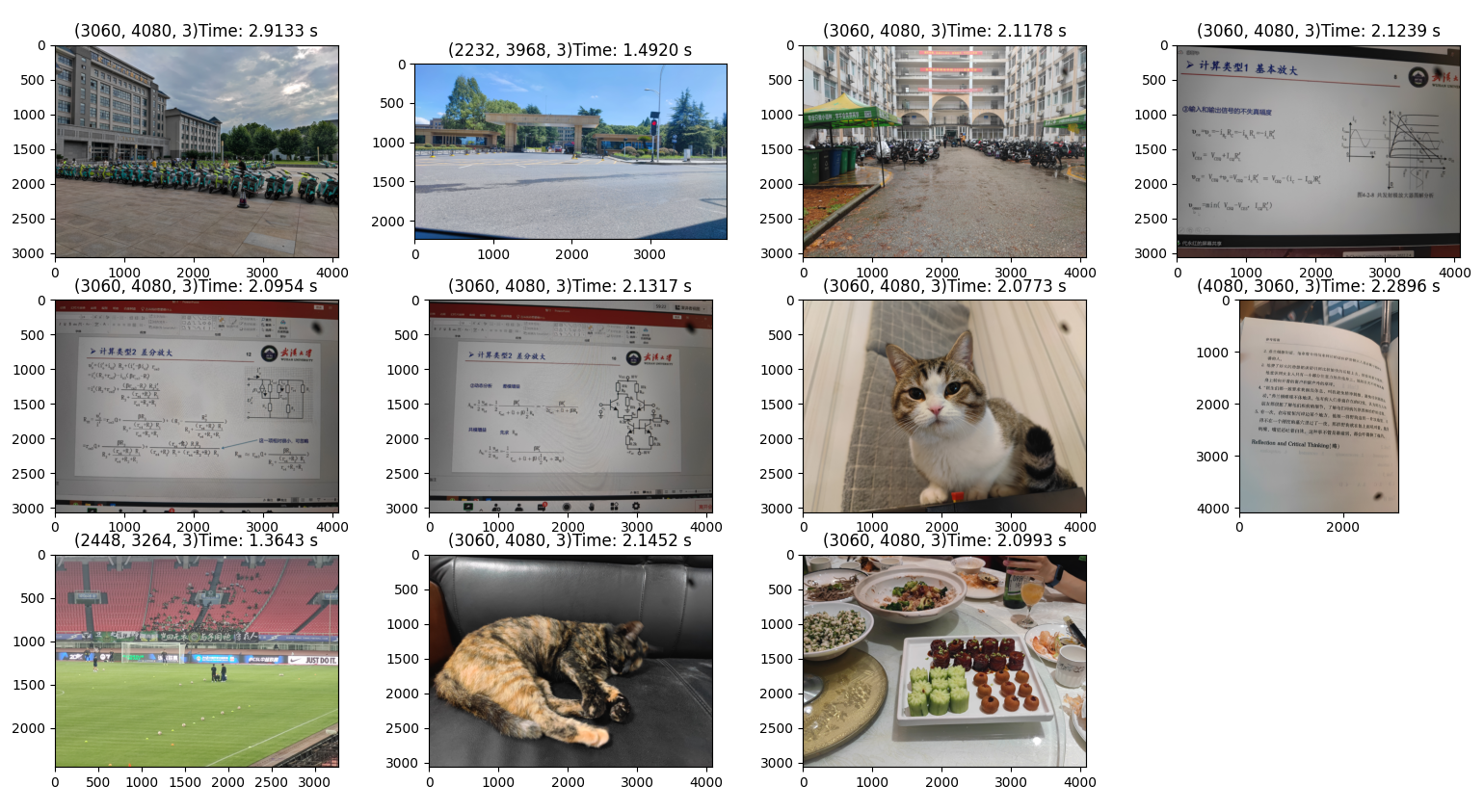

| 图片序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7×7卷积用时 | 2.91 | 1.49 | 2.11 | 2.12 | 2.09 | 2.13 | 2.07 | 2.22 | 1.36 | 2.14 | 2.09 |
| 359×359卷积用时 | 3.29 | 1.78 | 2.61 | 2.59 | 2.57 | 2.60 | 2.62 | 2.64 | 1.67 | 2.46 | 2.47 |
由实验数据可知,相同分辨率的在同一尺度下卷积没有太大的区别。这和FFT的具体实现有关系。例如Cooley–Tukey算法在素数矩阵上性能就会变差。
这份报告介绍了基于NumPy的FFT快速卷积算法。首先讨论了卷积在图像处理中的重要性,然后比较了不同实现方式的性能,包括OpenCV和SciPy自带的卷积函数。接着详细介绍了算法的实现过程,并通过实验对比了不同方法的性能表现。实验结果显示,在大尺寸卷积核情况下,FFT方法明显优于时域卷积。最后总结了实验数据,指出了不同尺寸矩阵对FFT算法性能的影响。整体而言,本文提出的基于NumPy的FFT快速卷积算法能够有效提高图像处理中卷积操作的计算速度。
[1] SciPy.signal.convolve — SciPy v1.12.0 手册
[2] NumPy FFT 性能提升|极客笔记 (deepinout.com)