404
+Page not found
+Page not found
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+# Set up model
+
+# Define flows
+K = 32
+torch.manual_seed(0)
+
+latent_size = 4
+b = torch.Tensor([1] * (latent_size // 2) + [0] * (latent_size // 2))
+flows = []
+for i in range(K):
+ s = nf.nets.MLP([latent_size, 4 * latent_size, latent_size], init_zeros=True)
+ t = nf.nets.MLP([latent_size, 4 * latent_size, latent_size], init_zeros=True)
+ if i % 2 == 0:
+ flows += [nf.flows.MaskedAffineFlow(b, t, s)]
+ else:
+ flows += [nf.flows.MaskedAffineFlow(1 - b, t, s)]
+ flows += [nf.flows.ActNorm(latent_size)]
+
+# Set augmented target
+target = nf.distributions.TwoIndependent(nf.distributions.TwoMoons(),
+ nf.distributions.DiagGaussian(2))
+# Set base distribution
+q0 = nf.distributions.DiagGaussian(4)
+
+# Construct flow model
+nfm = nf.NormalizingFlow(q0=q0, flows=flows, p=target)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+nfm = nfm.to(device)
+nfm = nfm.double()
+
+# Initialize ActNorm
+z, _ = nfm.sample(num_samples=2 ** 7)
+z_np = z.to('cpu').data.numpy()
+
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.title("Standard coordinates")
+plt.show()
+
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 2].flatten(), z_np[:, 3].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.title("Augmented coordinates")
+plt.show()
+# Plot augmented target
+z = target.sample(num_samples=2 ** 16)
+z_np = z.to('cpu').data.numpy()
+
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.title("Standard coordinates")
+plt.show()
+
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 2].flatten(), z_np[:, 3].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.title("Augmented coordinates")
+plt.show()
+# Train model
+max_iter = 20000
+num_samples = 2 * 10
+anneal_iter = 10000
+show_iter = 1000
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-4, weight_decay=1e-6)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+ loss = nfm.reverse_kld(num_samples, beta=np.min([1., 0.01 + it / anneal_iter]))
+
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned posterior
+ if (it + 1) % show_iter == 0:
+ z, _ = nfm.sample(num_samples=2 ** 14)
+ z_np = z.to('cpu').data.numpy()
+
+ plt.figure(figsize=(15, 15))
+ plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+ plt.gca().set_aspect('equal', 'box')
+ plt.title("Standard coordinates")
+ plt.show()
+
+ plt.figure(figsize=(15, 15))
+ plt.hist2d(z_np[:, 2].flatten(), z_np[:, 3].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+ plt.gca().set_aspect('equal', 'box')
+ plt.title("Augmented coordinates")
+ plt.show()
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot learned distribution
+z, _ = nfm.sample(num_samples=2 ** 16)
+z_np = z.to('cpu').data.numpy()
+
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.title("Standard coordinates")
+plt.show()
+
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 2].flatten(), z_np[:, 3].flatten(), (50, 50), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.title("Augmented coordinates")
+plt.show()
+This example shows how one can easily change the base distribution with our API. +First, let's look at how the normalizing flow can learn a two moons target distribution with a Gaussian distribution as the base.
+# Import packages
+import torch
+import numpy as np
+
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from mpl_toolkits.mplot3d import Axes3D
+from matplotlib import cm
+
+from tqdm import tqdm
+# Set up model
+
+# Define 2D Gaussian base distribution
+base = nf.distributions.base.DiagGaussian(2)
+
+# Define list of flows
+num_layers = 32
+flows = []
+for i in range(num_layers):
+ # Neural network with two hidden layers having 64 units each
+ # Last layer is initialized by zeros making training more stable
+ param_map = nf.nets.MLP([1, 64, 64, 2], init_zeros=True)
+ # Add flow layer
+ flows.append(nf.flows.AffineCouplingBlock(param_map))
+ # Swap dimensions
+ flows.append(nf.flows.Permute(2, mode='swap'))
+
+# Construct flow model
+model = nf.NormalizingFlow(base, flows)
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+# Define target distribution
+target = nf.distributions.TwoMoons()
+# Plot target distribution
+grid_size = 200
+xx, yy = torch.meshgrid(torch.linspace(-3, 3, grid_size), torch.linspace(-3, 3, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.to(device)
+
+log_prob = target.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Plot initial flow distribution
+model.eval()
+log_prob = model.log_prob(zz).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 4000
+num_samples = 2 ** 9
+show_iter = 500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=5e-4, weight_decay=1e-5)
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ x = target.sample(num_samples).to(device)
+
+ # Compute loss
+ loss = model.forward_kld(x)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ model.eval()
+ log_prob = model.log_prob(zz)
+ model.train()
+ prob = torch.exp(log_prob.to('cpu').view(*xx.shape))
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot target distribution
+f, ax = plt.subplots(1, 2, sharey=True, figsize=(15, 7))
+
+log_prob = target.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[0].pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+
+ax[0].set_aspect('equal', 'box')
+ax[0].set_axis_off()
+ax[0].set_title('Target', fontsize=24)
+
+# Plot learned distribution
+model.eval()
+log_prob = model.log_prob(zz).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[1].pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+
+ax[1].set_aspect('equal', 'box')
+ax[1].set_axis_off()
+ax[1].set_title('Real NVP', fontsize=24)
+
+plt.subplots_adjust(wspace=0.1)
+
+plt.show()
+Notice there is a bridge between the two modes of the learned target. +This is not a big deal usually since the bridge is really thin, and going to higher dimensional space will make it expoentially unlike to have samples within the bridge. +However, we can see the shape of each mode is also a bit distorted. +So it would be nice to get rid of the bridge. Now let's try to use a Gaussian mixture distribution as our base distribution, instead of a single Gaussian.
+# Set up model
+
+# Define a mixture of Gaussians with 2 modes.
+base = nf.distributions.base.GaussianMixture(2,2, loc=[[-2,0],[2,0]],scale=[[0.3,0.3],[0.3,0.3]])
+
+# Define list of flows
+num_layers = 32
+flows = []
+for i in range(num_layers):
+ # Neural network with two hidden layers having 64 units each
+ # Last layer is initialized by zeros making training more stable
+ param_map = nf.nets.MLP([1, 64, 64, 2], init_zeros=True)
+ # Add flow layer
+ flows.append(nf.flows.AffineCouplingBlock(param_map))
+ # Swap dimensions
+ flows.append(nf.flows.Permute(2, mode='swap'))
+
+# Construct flow model
+model = nf.NormalizingFlow(base, flows).cuda()
+# Plot initial flow distribution
+model.eval()
+log_prob = model.log_prob(zz).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 4000
+num_samples = 2 ** 9
+show_iter = 500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=5e-4, weight_decay=1e-5)
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ x = target.sample(num_samples).to(device)
+
+ # Compute loss
+ loss = model.forward_kld(x)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ model.eval()
+ log_prob = model.log_prob(zz)
+ model.train()
+ prob = torch.exp(log_prob.to('cpu').view(*xx.shape))
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+Now the modes are in better shape! And there is no bridge between the two modes!
+This is a Neural Spline Flow model which has circularand unbounded random variables combined in one random vector.
+# Import packages
+import torch
+import numpy as np
+
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+# Set up target
+class Target:
+ def __init__(self, ndim, ind_circ):
+ self.ndim = ndim
+ self.ind_circ = ind_circ
+
+ def sample(self, n):
+ s = torch.randn(n, self.ndim)
+ c = torch.rand(n, self.ndim) > 0.6
+ s = c * (0.3 * s - 0.5) + (1 - 1. * c) * (s + 1.3)
+ u = torch.rand(n, len(self.ind_circ))
+ s_ = torch.acos(2 * u - 1)
+ c = torch.rand(n, len(self.ind_circ)) > 0.3
+ s_[c] = -s_[c]
+ s[:, self.ind_circ] = (s_ + 1) % (2 * np.pi) - np.pi
+ return s
+
+# Visualize target
+target = Target(2, [1])
+s = target.sample(1000000)
+plt.hist(s[:, 0].data.numpy(), bins=200)
+plt.show()
+plt.hist(s[:, 1].data.numpy(), bins=200)
+plt.show()
+base = nf.distributions.UniformGaussian(2, [1], torch.tensor([1., 2 * np.pi]))
+
+# Visualize base
+s = base.sample(1000000)
+plt.hist(s[:, 0].data.numpy(), bins=200)
+plt.show()
+plt.hist(s[:, 1].data.numpy(), bins=200)
+plt.show()
+# Create normalizing flow
+K = 20
+
+flow_layers = []
+for i in range(K):
+ flow_layers += [nf.flows.CircularAutoregressiveRationalQuadraticSpline(2, 1, 128, [1],
+ tail_bound=torch.tensor([5., np.pi]),
+ permute_mask=True)]
+
+model = nf.NormalizingFlow(base, flow_layers)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+model.eval()
+with torch.no_grad():
+ s, _ = model.sample(50000)
+model.train()
+plt.hist(s[:, 0].cpu().data.numpy(), bins=100)
+plt.show()
+plt.hist(s[:, 1].cpu().data.numpy(), bins=100)
+plt.show()
+# Train model
+max_iter = 20000
+num_samples = 2 ** 10
+show_iter = 5000
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=1e-4, weight_decay=1e-4)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ x = target.sample(num_samples)
+
+ # Compute loss
+ loss = model.forward_kld(x.to(device))
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned density
+ if (it + 1) % show_iter == 0:
+ model.eval()
+ with torch.no_grad():
+ s, _ = model.sample(50000)
+ model.train()
+ plt.hist(s[:, 0].cpu().data.numpy(), bins=100)
+ plt.show()
+ plt.hist((s[:, 1].cpu().data.numpy() - 1) % (2 * np.pi), bins=100)
+ plt.show()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+In this notebook, we train normalizing flows to fit predefined prior distributions, testing their expressivity. The plots are generated to visualize the learned distributions for given layers $K$, and the training loss is plotted to compare the expressivity of different flows.
+%load_ext autoreload
+%autoreload 2
+
+# Import required packages
+import torch
+import numpy as np
+
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+
+print("PyTorch version: %s" % torch.__version__)
+dev = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
+print("Using device: %s" % dev)
+
+#z shape is (batch_size, num_samples, dim)
+priors = []
+priors.append(nf.distributions.TwoModes(2.0, 0.2))
+priors.append(nf.distributions.Sinusoidal(0.4, 4))
+priors.append(nf.distributions.Sinusoidal_gap(0.4, 4))
+priors.append(nf.distributions.Sinusoidal_split(0.4, 4))
+priors.append(nf.distributions.Smiley(0.15))
+
+
+# Plot prior distributions
+grid_size = 200
+grid_length = 4.0
+grid_shape = ([-grid_length, grid_length], [-grid_length, grid_length])
+
+space_mesh = torch.linspace(-grid_length, grid_length, grid_size)
+xx, yy = torch.meshgrid(space_mesh, space_mesh)
+z = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2)
+z = z.reshape(-1, 2)
+
+K_arr = [2, 8, 32]
+max_iter = 30000
+batch_size = 512
+num_samples = 256
+save_iter = 1000
+
+for k in range(len(priors)):
+ log_prob = priors[k].log_prob(z)
+ prob = torch.exp(log_prob)
+
+ plt.figure(figsize=(10, 10))
+ plt.pcolormesh(xx, yy, prob.reshape(grid_size, grid_size))
+ plt.show()
+flow_types = ("Planar", "Radial", "NICE", "RealNVP")
+max_iter = 20000
+batch_size = 1024
+plot_batches = 10 ** 2
+plot_samples = 10 ** 4
+save_iter = 50
+
+for name in flow_types:
+ K_arr = [2, 8, 32]
+ for K in K_arr:
+ print("Flow type {} with K = {}".format(name, K))
+ for k in range(len(priors)):
+ if k == 0 or k == 4:
+ anneal_iter = 10000
+ else: # turn annealing off when fitting to sinusoidal distributions
+ anneal_iter = 1
+
+ flows = []
+ b = torch.tensor([0,1])
+ for i in range(K):
+ if name == "Planar":
+ flows += [nf.flows.Planar((2,))]
+ elif name == "Radial":
+ flows += [nf.flows.Radial((2,))]
+ elif name == "NICE":
+ flows += [nf.flows.MaskedAffineFlow(b, nf.nets.MLP([2, 16, 16, 2], init_zeros=True))]
+ elif name == "RealNVP":
+ flows += [nf.flows.MaskedAffineFlow(b, nf.nets.MLP([2, 16, 16, 2], init_zeros=True),
+ nf.nets.MLP([2, 16, 16, 2], init_zeros=True))]
+ b = 1-b # parity alternation for mask
+
+ q0 = nf.distributions.DiagGaussian(2)
+ nfm = nf.NormalizingFlow(p=priors[k], q0=q0, flows=flows)
+ nfm.to(dev) # Move model on GPU if available
+
+ # Train model
+ loss_hist = np.array([])
+ log_q_hist = np.array([])
+ log_p_hist = np.array([])
+ x = torch.zeros(batch_size, device=dev)
+
+ optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-3, weight_decay=1e-3)
+ for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+ loss = nfm.reverse_kld(batch_size, np.min([1.0, 0.01 + it / anneal_iter]))
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ if (it + 1) % save_iter == 0:
+ loss_hist = np.append(loss_hist, loss.cpu().data.numpy())
+
+ # Plot learned posterior distribution
+ z_np = np.zeros((0, 2))
+ for i in range(plot_batches):
+ z, _ = nfm.sample(plot_samples)
+ z_np = np.concatenate((z_np, z.cpu().data.numpy()))
+ plt.figure(figsize=(10, 10))
+ plt.hist2d(z_np[:, 0], z_np[:, 1], (grid_size, grid_size), grid_shape)
+ plt.show()
+ np.save("{}-K={}-k={}".format(name,K,k), (z_np, loss.cpu().data.numpy()))
+
+ # Plot training history
+ plt.figure(figsize=(10, 10))
+ plt.plot(loss_hist, label='loss')
+ plt.legend()
+ plt.show()
+fig = plt.figure(figsize=(14, 10))
+K_arr = [2, 8, 32]
+nrows=5
+ncols=7
+axes = [ fig.add_subplot(nrows, ncols, r * ncols + c + 1) for r in range(0, nrows) for c in range(0, ncols) ]
+
+for ax in axes:
+ ax.set_xticks([])
+ ax.set_yticks([])
+
+grid_size = 100
+grid_length = 4.0
+grid_shape = ([-grid_length, grid_length], [-grid_length, grid_length])
+
+space_mesh = torch.linspace(-grid_length, grid_length, grid_size)
+xx, yy = torch.meshgrid(space_mesh, space_mesh)
+z = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2)
+z = z.reshape(-1, 2)
+axes[0].annotate('Target', xy=(0.5, 1.10), xytext=(0.5, 1.20), xycoords='axes fraction',
+ fontsize=24, ha='center', va='bottom',
+ arrowprops=dict(arrowstyle='-[, widthB=1.5, lengthB=0.2', lw=2.0))
+for k in range(5):
+ axes[k*ncols].set_ylabel('{}'.format(k+1), rotation=0, fontsize=20, labelpad=15)
+ log_prob = priors[k].log_prob(z)
+ prob = torch.exp(log_prob)
+ axes[k*ncols + 0].pcolormesh(xx, yy, prob.reshape(grid_size, grid_size))
+
+
+for l in range(len(K_arr)):
+ K = K_arr[l]
+ if l == 1:
+ axes[0*ncols + l+1].annotate('Planar flows', xy=(0.5, 1.10), xytext=(0.5, 1.20), xycoords='axes fraction',
+ fontsize=24, ha='center', va='bottom',
+ arrowprops=dict(arrowstyle='-[, widthB=6.0, lengthB=0.2', lw=2.0))
+ axes[4*ncols + l+1].set_xlabel('K = {}'.format(K), fontsize=20)
+ for k in range(5):
+ z_np, _ = np.load("Planar-K={}-k={}.npy".format(K,k), allow_pickle=True)
+ axes[k*ncols + l+1].hist2d(z_np[:, 0], z_np[:, 1], (grid_size, grid_size), grid_shape)
+
+for l in range(len(K_arr)):
+ K = K_arr[l]
+ if l == 1:
+ axes[0*ncols + l+1+len(K_arr)].annotate('Radial flows', xy=(0.5, 1.10), xytext=(0.5, 1.20), xycoords='axes fraction',
+ fontsize=24, ha='center', va='bottom',
+ arrowprops=dict(arrowstyle='-[, widthB=6.0, lengthB=0.2', lw=2.0))
+ axes[4*ncols + l+1+len(K_arr)].set_xlabel('K = {}'.format(K), fontsize=20)
+ for k in range(5):
+ z_np, _ = np.load("Radial-K={}-k={}.npy".format(K,k), allow_pickle=True)
+ axes[k*ncols + l+1+len(K_arr)].hist2d(z_np[:, 0], z_np[:, 1], (grid_size, grid_size), grid_shape)
+
+fig.subplots_adjust(hspace=0.02, wspace=0.02)
+
+for l in range(1,4):
+ for k in range(5):
+ pos1 = axes[k*ncols + l].get_position() # get the original position
+ pos2 = [pos1.x0 + 0.01, pos1.y0, pos1.width, pos1.height]
+ axes[k*ncols + l].set_position(pos2) # set a new position
+
+for l in range(4,7):
+ for k in range(5):
+ pos1 = axes[k*ncols + l].get_position() # get the original position
+ pos2 = [pos1.x0 + 0.02, pos1.y0, pos1.width, pos1.height]
+ axes[k*ncols + l].set_position(pos2) # set a new position
+from itertools import repeat
+
+k_arr = [0, 2, 4]
+fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))
+markers = ['s', 'o', 'v', 'P', 'd']
+
+for k in range(len(k_arr)):
+ loss = [[] for i in repeat(None, len(flow_types))]
+ for intt, name in enumerate(flow_types):
+ for K in K_arr:
+ _, loss_v = np.load("{}-K={}-k={}.npy".format(name,K,k), allow_pickle=True)
+ loss[intt].append(loss_v)
+ axes[k].plot(K_arr, loss[intt], marker=markers[intt], label=name)
+ axes[k].set_title('Target {}'.format(k_arr[k]+1), fontsize=16)
+ axes[k].set_xlabel('Flow length', fontsize=12)
+ axes[k].set_ylabel('Variational bound (nats)', fontsize=12)
+ axes[k].legend()
+ axes[k].grid('major')
+
+fig.tight_layout(pad=2.0)
+Here, we train a conditional normalizing flow model $q(x|c)$. Our target $p(x|c)$ is a simple 2D Gaussian $\mathcal{N}(x|\mu, \sigma)$, where we condition on the mean $\mu$ and standard deviation $\sigma$, i.e. $c = (\mu, \sigma)$. We apply conditional autoregressive and coupling neural spline flows as well as a conditional masked autoregressive flow to the problem.
+# Import packages
+import torch
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+
+from tqdm import tqdm
+# Get device to be used
+device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
+# Define target
+target = nf.distributions.target.ConditionalDiagGaussian()
+context_size = 4
+
+# Plot target
+grid_size = 100
+xx, yy = torch.meshgrid(torch.linspace(-2, 2, grid_size), torch.linspace(-2, 2, grid_size), indexing='ij')
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.to(device)
+context_plot = torch.cat([torch.tensor([0.3, 0.9]).to(device) + torch.zeros_like(zz),
+ 0.6 * torch.ones_like(zz)], dim=-1)
+logp = target.log_prob(zz, context_plot)
+p_target = torch.exp(logp).view(*xx.shape).cpu().data.numpy()
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, p_target, shading='auto')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Define flows
+K = 4
+
+latent_size = 2
+hidden_units = 128
+hidden_layers = 2
+
+flows = []
+for i in range(K):
+ flows += [nf.flows.AutoregressiveRationalQuadraticSpline(latent_size, hidden_layers, hidden_units,
+ num_context_channels=context_size)]
+ flows += [nf.flows.LULinearPermute(latent_size)]
+
+# Set base distribution
+q0 = nf.distributions.DiagGaussian(2, trainable=False)
+
+# Construct flow model
+model = nf.ConditionalNormalizingFlow(q0, flows, target)
+
+# Move model on GPU if available
+model = model.to(device)
+# Plot initial flow distribution, target as contours
+model.eval()
+log_prob = model.log_prob(zz, context_plot).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy(), shading='auto')
+plt.contour(xx, yy, p_target, cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 5000
+batch_size= 128
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=3e-4, weight_decay=1e-5)
+
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ context = torch.cat([torch.randn((batch_size, 2), device=device),
+ 0.5 + 0.5 * torch.rand((batch_size, 2), device=device)],
+ dim=-1)
+ x = target.sample(batch_size, context)
+
+ # Compute loss
+ loss = model.forward_kld(x, context)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+100%|████████████████████████████████████████████████████████████| 5000/5000 [01:34<00:00, 52.69it/s] ++
# Plot trained flow distribution, target as contours
+model.eval()
+log_prob = model.log_prob(zz, context_plot).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy(), shading='auto')
+plt.contour(xx, yy, p_target, cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Define flows
+K = 4
+
+latent_size = 2
+hidden_units = 128
+hidden_layers = 2
+
+flows = []
+for i in range(K):
+ flows += [nf.flows.CoupledRationalQuadraticSpline(latent_size, hidden_layers, hidden_units,
+ num_context_channels=context_size)]
+ flows += [nf.flows.LULinearPermute(latent_size)]
+
+# Set base distribution
+q0 = nf.distributions.DiagGaussian(2, trainable=False)
+
+# Construct flow model
+model = nf.ConditionalNormalizingFlow(q0, flows, target)
+
+# Move model on GPU if available
+model = model.to(device)
+# Plot initial flow distribution, target as contours
+model.eval()
+log_prob = model.log_prob(zz, context_plot).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy(), shading='auto')
+plt.contour(xx, yy, p_target, cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 5000
+batch_size= 128
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=3e-4, weight_decay=1e-5)
+
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ context = torch.cat([torch.randn((batch_size, 2), device=device),
+ 0.5 + 0.5 * torch.rand((batch_size, 2), device=device)],
+ dim=-1)
+ x = target.sample(batch_size, context)
+
+ # Compute loss
+ loss = model.forward_kld(x, context)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+100%|████████████████████████████████████████████████████████████| 5000/5000 [02:16<00:00, 36.51it/s] ++
# Plot trained flow distribution, target as contours
+model.eval()
+log_prob = model.log_prob(zz, context_plot).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy(), shading='auto')
+plt.contour(xx, yy, p_target, cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Define flows
+K = 4
+
+latent_size = 2
+hidden_units = 128
+num_blocks = 2
+
+flows = []
+for i in range(K):
+ flows += [nf.flows.MaskedAffineAutoregressive(latent_size, hidden_units,
+ context_features=context_size,
+ num_blocks=num_blocks)]
+ flows += [nf.flows.LULinearPermute(latent_size)]
+
+# Set base distribution
+q0 = nf.distributions.DiagGaussian(2, trainable=False)
+
+# Construct flow model
+model = nf.ConditionalNormalizingFlow(q0, flows, target)
+
+# Move model on GPU if available
+model = model.to(device)
+# Plot initial flow distribution, target as contours
+model.eval()
+log_prob = model.log_prob(zz, context_plot).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy(), shading='auto')
+plt.contour(xx, yy, p_target, cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 5000
+batch_size= 128
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-5)
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ context = torch.cat([torch.randn((batch_size, 2), device=device),
+ 0.5 + 0.5 * torch.rand((batch_size, 2), device=device)],
+ dim=-1)
+ x = target.sample(batch_size, context)
+
+ # Compute loss
+ loss = model.forward_kld(x, context)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+100%|████████████████████████████████████████████████████████████| 5000/5000 [02:00<00:00, 41.53it/s] ++
# Plot trained flow distribution, target as contours
+model.eval()
+log_prob = model.log_prob(zz, context_plot).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy(), shading='auto')
+plt.contour(xx, yy, p_target, cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Import required packages
+import torch
+import torchvision as tv
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+# Set up model
+
+# Define flows
+L = 3
+K = 16
+torch.manual_seed(0)
+
+input_shape = (3, 32, 32)
+n_dims = np.prod(input_shape)
+channels = 3
+hidden_channels = 256
+split_mode = 'channel'
+scale = True
+num_classes = 10
+
+# Set up flows, distributions and merge operations
+q0 = []
+merges = []
+flows = []
+for i in range(L):
+ flows_ = []
+ for j in range(K):
+ flows_ += [nf.flows.GlowBlock(channels * 2 ** (L + 1 - i), hidden_channels,
+ split_mode=split_mode, scale=scale)]
+ flows_ += [nf.flows.Squeeze()]
+ flows += [flows_]
+ if i > 0:
+ merges += [nf.flows.Merge()]
+ latent_shape = (input_shape[0] * 2 ** (L - i), input_shape[1] // 2 ** (L - i),
+ input_shape[2] // 2 ** (L - i))
+ else:
+ latent_shape = (input_shape[0] * 2 ** (L + 1), input_shape[1] // 2 ** L,
+ input_shape[2] // 2 ** L)
+ q0 += [nf.distributions.ClassCondDiagGaussian(latent_shape, num_classes)]
+
+
+# Construct flow model with the multiscale architecture
+model = nf.MultiscaleFlow(q0, flows, merges)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+# Prepare training data
+batch_size = 128
+
+transform = tv.transforms.Compose([tv.transforms.ToTensor(), nf.utils.Scale(255. / 256.), nf.utils.Jitter(1 / 256.)])
+train_data = tv.datasets.CIFAR10('datasets/', train=True,
+ download=True, transform=transform)
+train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, shuffle=True,
+ drop_last=True)
+
+test_data = tv.datasets.CIFAR10('datasets/', train=False,
+ download=True, transform=transform)
+test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size)
+
+train_iter = iter(train_loader)
+# Train model
+max_iter = 20000
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adamax(model.parameters(), lr=1e-3, weight_decay=1e-5)
+
+for i in tqdm(range(max_iter)):
+ try:
+ x, y = next(train_iter)
+ except StopIteration:
+ train_iter = iter(train_loader)
+ x, y = next(train_iter)
+ optimizer.zero_grad()
+ loss = model.forward_kld(x.to(device), y.to(device))
+
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ loss_hist = np.append(loss_hist, loss.detach().to('cpu').numpy())
+ del(x, y, loss)
+
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Model samples
+num_sample = 10
+
+with torch.no_grad():
+ y = torch.arange(num_classes).repeat(num_sample).to(device)
+ x, _ = model.sample(y=y)
+ x_ = torch.clamp(x, 0, 1)
+ plt.figure(figsize=(10, 10))
+ plt.imshow(np.transpose(tv.utils.make_grid(x_, nrow=num_classes).cpu().numpy(), (1, 2, 0)))
+ plt.show()
+# Get bits per dim
+n = 0
+bpd_cum = 0
+with torch.no_grad():
+ for x, y in iter(test_loader):
+ nll = model(x.to(device), y.to(device))
+ nll_np = nll.cpu().numpy()
+ bpd_cum += np.nansum(nll_np / np.log(2) / n_dims + 8)
+ n += len(x) - np.sum(np.isnan(nll_np))
+
+ print('Bits per dim: ', bpd_cum / n)
+Here, we show how a flow can be trained to generate images with the normflows package. The flow is a class-conditional Glow model, which is based on the multi-scale architecture. This Glow model is applied to the CIFAR-10 dataset.
To get started, we have to install the normflows package.
!pip install normflows
+# Import required packages
+import torch
+import torchvision as tv
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+Now that we imported the necessary packages, we create a flow model. Glow consists of nf.flows.GlowBlocks, that are arranged in a nf.MultiscaleFlow, following the multi-scale architecture. The base distribution is a nf.distributions.ClassCondDiagGaussian, which is a diagonal Gaussian with mean and standard deviation dependent on the class label of the image.
# Set up model
+
+# Define flows
+L = 3
+K = 16
+torch.manual_seed(0)
+
+input_shape = (3, 32, 32)
+n_dims = np.prod(input_shape)
+channels = 3
+hidden_channels = 256
+split_mode = 'channel'
+scale = True
+num_classes = 10
+
+# Set up flows, distributions and merge operations
+q0 = []
+merges = []
+flows = []
+for i in range(L):
+ flows_ = []
+ for j in range(K):
+ flows_ += [nf.flows.GlowBlock(channels * 2 ** (L + 1 - i), hidden_channels,
+ split_mode=split_mode, scale=scale)]
+ flows_ += [nf.flows.Squeeze()]
+ flows += [flows_]
+ if i > 0:
+ merges += [nf.flows.Merge()]
+ latent_shape = (input_shape[0] * 2 ** (L - i), input_shape[1] // 2 ** (L - i),
+ input_shape[2] // 2 ** (L - i))
+ else:
+ latent_shape = (input_shape[0] * 2 ** (L + 1), input_shape[1] // 2 ** L,
+ input_shape[2] // 2 ** L)
+ q0 += [nf.distributions.ClassCondDiagGaussian(latent_shape, num_classes)]
+
+
+# Construct flow model with the multiscale architecture
+model = nf.MultiscaleFlow(q0, flows, merges)
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+With torchvision we can download the CIFAR-10 dataset.
# Prepare training data
+batch_size = 128
+
+transform = tv.transforms.Compose([tv.transforms.ToTensor(), nf.utils.Scale(255. / 256.), nf.utils.Jitter(1 / 256.)])
+train_data = tv.datasets.CIFAR10('datasets/', train=True,
+ download=True, transform=transform)
+train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, shuffle=True,
+ drop_last=True)
+
+test_data = tv.datasets.CIFAR10('datasets/', train=False,
+ download=True, transform=transform)
+test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size)
+
+train_iter = iter(train_loader)
+Now, can train the model on the image data.
+# Train model
+max_iter = 20000
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adamax(model.parameters(), lr=1e-3, weight_decay=1e-5)
+
+for i in tqdm(range(max_iter)):
+ try:
+ x, y = next(train_iter)
+ except StopIteration:
+ train_iter = iter(train_loader)
+ x, y = next(train_iter)
+ optimizer.zero_grad()
+ loss = model.forward_kld(x.to(device), y.to(device))
+
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ loss_hist = np.append(loss_hist, loss.detach().to('cpu').numpy())
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+To evaluate our model, we first draw samples from our model. When sampling, we can specify the classes, so we draw then samples from each class.
+# Model samples
+num_sample = 10
+
+with torch.no_grad():
+ y = torch.arange(num_classes).repeat(num_sample).to(device)
+ x, _ = model.sample(y=y)
+ x_ = torch.clamp(x, 0, 1)
+ plt.figure(figsize=(10, 10))
+ plt.imshow(np.transpose(tv.utils.make_grid(x_, nrow=num_classes).cpu().numpy(), (1, 2, 0)))
+ plt.show()
+For quantitative evaluation, we can compute the bits per dim of our model.
+# Get bits per dim
+n = 0
+bpd_cum = 0
+with torch.no_grad():
+ for x, y in iter(test_loader):
+ nll = model(x.to(device), y.to(device))
+ nll_np = nll.cpu().numpy()
+ bpd_cum += np.nansum(nll_np / np.log(2) / n_dims + 8)
+ n += len(x) - np.sum(np.isnan(nll_np))
+
+ print('Bits per dim: ', bpd_cum / n)
+Note that to get competitive performance, a much larger model then specified in this notebook, which is trained over 100 thousand to 1 million iterations, is needed.
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+# Set up model
+
+# Define flows
+K = 32
+#torch.manual_seed(0)
+
+b = torch.tensor([0, 1])
+flows = []
+for i in range(K):
+ s = nf.nets.MLP([2, 4, 4, 2])
+ t = nf.nets.MLP([2, 4, 4, 2])
+ if i % 2 == 0:
+ flows += [nf.flows.MaskedAffineFlow(b, t, s)]
+ else:
+ flows += [nf.flows.MaskedAffineFlow(1 - b, t, s)]
+
+# Set target and base distribution
+img = 1 - plt.imread('img.png')[:, :, 0] # Specify the path to your image here
+target = nf.distributions.ImagePrior(img)
+q0 = nf.distributions.DiagGaussian(2)
+
+# Construct flow model
+nfm = nf.NormalizingFlow(q0=q0, flows=flows, p=target)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+nfm = nfm.to(device)
+nfm = nfm.double()
+# Plot prior distribution
+grid_size = 200
+xx, yy = torch.meshgrid(torch.linspace(-3, 3, grid_size), torch.linspace(-3, 3, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.double().to(device)
+log_prob = target.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.show()
+
+# Plot initial posterior distribution
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.show()
+# Train model
+max_iter = 10000
+num_samples = 2 * 16
+show_iter = 2000
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-4, weight_decay=1e-4)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+ x = nfm.p.sample(num_samples).double()
+ loss = nfm.forward_kld(x)
+ loss.backward()
+ optimizer.step()
+
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+ prob = torch.exp(log_prob)
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(10, 10))
+ plt.pcolormesh(xx, yy, prob.data.numpy())
+ plt.show()
+
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot learned distribution
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.show()
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from sklearn.datasets import make_moons
+
+from matplotlib import pyplot as plt
+
+from tqdm import tqdm
+# Set up model
+
+# Define flows
+K = 16
+torch.manual_seed(0)
+
+latent_size = 2
+hidden_units = 128
+hidden_layers = 2
+
+flows = []
+for i in range(K):
+ flows += [nf.flows.AutoregressiveRationalQuadraticSpline(latent_size, hidden_layers, hidden_units)]
+ flows += [nf.flows.LULinearPermute(latent_size)]
+
+# Set base distribuiton
+q0 = nf.distributions.DiagGaussian(2, trainable=False)
+
+# Construct flow model
+nfm = nf.NormalizingFlow(q0=q0, flows=flows)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+nfm = nfm.to(device)
+# Plot target distribution
+x_np, _ = make_moons(2 ** 20, noise=0.1)
+plt.figure(figsize=(15, 15))
+plt.hist2d(x_np[:, 0], x_np[:, 1], bins=200)
+plt.show()
+
+# Plot initial flow distribution
+grid_size = 100
+xx, yy = torch.meshgrid(torch.linspace(-1.5, 2.5, grid_size), torch.linspace(-2, 2, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.to(device)
+
+nfm.eval()
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+nfm.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 10000
+num_samples = 2 ** 9
+show_iter = 500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-3, weight_decay=1e-5)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ x_np, _ = make_moons(num_samples, noise=0.1)
+ x = torch.tensor(x_np).float().to(device)
+
+ # Compute loss
+ loss = nfm.forward_kld(x)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ nfm.eval()
+ log_prob = nfm.log_prob(zz)
+ nfm.train()
+ prob = torch.exp(log_prob.to('cpu').view(*xx.shape))
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(xx, yy, prob.data.numpy())
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot learned distribution
+nfm.eval()
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+nfm.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+We aim to approximate a distribution having as circular and a normal coordinate. To construct such a case, let $x$ be the normal (unbound) coordinate follow a standard normal distribution, i.e. +$$ p(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} x ^ 2}.$$ +The circular random variable $\phi$ follows a von Mises distribution given by +$$ p(\phi|x) = \frac{1}{2\pi I_0(1)} e^{\cos(\phi-\mu(x))}, $$ +where $I_0$ is the $0^\text{th}$ order Bessel function of the first kind and we set $\mu(x) = 3x$. Hence, our full target is given by +$$ p(x, \phi) = p(x)p(\phi|x) = \frac{1}{(2\pi)^{\frac{3}{2}} I_0(1)} e^{-\frac{1}{2} x ^ 2 + \cos(\phi-3x)}. $$ +We use a neural spline flow that models the two coordinates accordingly.
+# Import packages
+import torch
+import numpy as np
+
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from mpl_toolkits.mplot3d import Axes3D
+from matplotlib import cm
+
+from tqdm import tqdm
+This is our target $p(x, \phi)$.
+# Set up target
+class GaussianVonMises(nf.distributions.Target):
+ def __init__(self):
+ super().__init__(prop_scale=torch.tensor(2 * np.pi),
+ prop_shift=torch.tensor(-np.pi))
+ self.n_dims = 2
+ self.max_log_prob = -1.99
+ self.log_const = -1.5 * np.log(2 * np.pi) - np.log(np.i0(1))
+
+ def log_prob(self, x):
+ return -0.5 * x[:, 0] ** 2 + torch.cos(x[:, 1] - 3 * x[:, 0]) + self.log_const
+target = GaussianVonMises()
+# Plot target
+grid_size = 300
+xx, yy = torch.meshgrid(torch.linspace(-2.5, 2.5, grid_size), torch.linspace(-np.pi, np.pi, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+
+log_prob = target.log_prob(zz).view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+base = nf.distributions.UniformGaussian(2, [1], torch.tensor([1., 2 * np.pi]))
+
+K = 12
+
+flow_layers = []
+for i in range(K):
+ flow_layers += [nf.flows.CircularAutoregressiveRationalQuadraticSpline(2, 1, 512, [1], num_bins=10,
+ tail_bound=torch.tensor([5., np.pi]),
+ permute_mask=True)]
+
+model = nf.NormalizingFlow(base, flow_layers, target)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+# Plot model
+log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 10000
+num_samples = 2 ** 14
+show_iter = 2500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=5e-4)
+scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, max_iter)
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Compute loss
+ loss = model.reverse_kld(num_samples)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned model
+ if (it + 1) % show_iter == 0:
+ model.eval()
+ with torch.no_grad():
+ log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+ model.train()
+ prob = torch.exp(log_prob)
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+ # Iterate scheduler
+ scheduler.step()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# 2D plot
+f, ax = plt.subplots(1, 2, sharey=True, figsize=(15, 7))
+
+log_prob = target.log_prob(zz).view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[0].pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+ax[0].set_aspect('equal', 'box')
+
+ax[0].set_xticks(ticks=[-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
+ax[0].set_xticklabels(['$-\pi$', r'$-\frac{\pi}{2}$', '$0$', r'$\frac{\pi}{2}$', '$\pi$'],
+ fontsize=20)
+ax[0].set_yticks(ticks=[-2, -1, 0, 1, 2])
+ax[0].set_yticklabels(['$-2$', '$-1$', '$0$', '$1$', '$2$'],
+ fontsize=20)
+ax[0].set_xlabel('$\phi$', fontsize=24)
+ax[0].set_ylabel('$x$', fontsize=24)
+
+ax[0].set_title('Target', fontsize=24)
+
+log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[1].pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+ax[1].set_aspect('equal', 'box')
+
+ax[1].set_xticks(ticks=[-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
+ax[1].set_xticklabels(['$-\pi$', r'$-\frac{\pi}{2}$', '$0$', r'$\frac{\pi}{2}$', '$\pi$'],
+ fontsize=20)
+ax[1].set_xlabel('$\phi$', fontsize=24)
+
+ax[1].set_title('Neural Spline Flow', fontsize=24)
+
+plt.subplots_adjust(wspace=0.1)
+
+plt.show()
+# 3D plot
+fig = plt.figure(figsize=(15, 7))
+ax1 = fig.add_subplot(1, 2, 1, projection='3d')
+ax2 = fig.add_subplot(1, 2, 2, projection='3d')
+
+phi = np.linspace(-np.pi, np.pi, grid_size)
+z = np.linspace(-2.5, 2.5, grid_size)
+
+# create the surface
+x = np.outer(np.ones(grid_size), np.cos(phi))
+y = np.outer(np.ones(grid_size), np.sin(phi))
+z = np.outer(z, np.ones(grid_size))
+
+# Target
+log_prob = target.log_prob(zz).view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+prob_vis = prob / torch.max(prob)
+myheatmap = prob_vis.data.numpy()
+
+ax1._axis3don = False
+ax1.plot_surface(x, y, z, cstride=1, rstride=1, facecolors=cm.coolwarm(myheatmap), shade=False)
+
+ax1.set_title('Target', fontsize=24, y=0.97, pad=0)
+
+# Model
+log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+prob_vis = prob / torch.max(prob)
+myheatmap = prob_vis.data.numpy()
+
+ax2._axis3don = False
+ax2.plot_surface(x, y, z, cstride=1, rstride=1, facecolors=cm.coolwarm(myheatmap), shade=False)
+
+t = ax2.set_title('Neural Spline Flow', fontsize=24, y=0.97, pad=0)
+
+plt.subplots_adjust(wspace=-0.4)
+
+plt.show()
+This is the example we consider in our paper about the normflows package.
We aim to approximate a distribution having as circular and a normal coordinate. To construct such a case, let $x$ be the normal (unbound) coordinate follow a standard normal distribution, i.e. +$$ p(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} x ^ 2}.$$ +The circular random variable $\phi$ follows a von Mises distribution given by +$$ p(\phi|x) = \frac{1}{2\pi I_0(1)} e^{\cos(\phi-\mu(x))}, $$ +where $I_0$ is the $0^\text{th}$ order Bessel function of the first kind and we set $\mu(x) = 3x$. Hence, our full target is given by +$$ p(x, \phi) = p(x)p(\phi|x) = \frac{1}{(2\pi)^{\frac{3}{2}} I_0(1)} e^{-\frac{1}{2} x ^ 2 + \cos(\phi-3x)}. $$ +We use a neural spline flow that models the two coordinates accordingly.
+# Install normflows in Colab
+!pip install normflows
+# Import packages
+import torch
+import numpy as np
+
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from mpl_toolkits.mplot3d import Axes3D
+from matplotlib import cm
+
+from tqdm import tqdm
+This is our target $p(x, \phi)$.
+# Set up target
+class GaussianVonMises(nf.distributions.Target):
+ def __init__(self):
+ super().__init__(prop_scale=torch.tensor(2 * np.pi),
+ prop_shift=torch.tensor(-np.pi))
+ self.n_dims = 2
+ self.max_log_prob = -1.99
+ self.log_const = -1.5 * np.log(2 * np.pi) - np.log(np.i0(1))
+
+ def log_prob(self, x):
+ return -0.5 * x[:, 0] ** 2 + torch.cos(x[:, 1] - 3 * x[:, 0]) + self.log_const
+target = GaussianVonMises()
+# Plot target
+grid_size = 300
+xx, yy = torch.meshgrid(torch.linspace(-2.5, 2.5, grid_size), torch.linspace(-np.pi, np.pi, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+
+log_prob = target.log_prob(zz).view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+base = nf.distributions.UniformGaussian(2, [1], torch.tensor([1., 2 * np.pi]))
+
+K = 12
+
+flow_layers = []
+for i in range(K):
+ flow_layers += [nf.flows.CircularAutoregressiveRationalQuadraticSpline(2, 1, 512, [1], num_bins=10,
+ tail_bound=torch.tensor([5., np.pi]),
+ permute_mask=True)]
+
+model = nf.NormalizingFlow(base, flow_layers, target)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+# Plot model
+log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 10000
+num_samples = 2 ** 14
+show_iter = 2500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=5e-4)
+scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, max_iter)
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Compute loss
+ loss = model.reverse_kld(num_samples)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned model
+ if (it + 1) % show_iter == 0:
+ model.eval()
+ with torch.no_grad():
+ log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+ model.train()
+ prob = torch.exp(log_prob)
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+ # Iterate scheduler
+ scheduler.step()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# 2D plot
+f, ax = plt.subplots(1, 2, sharey=True, figsize=(15, 7))
+
+log_prob = target.log_prob(zz).view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[0].pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+ax[0].set_aspect('equal', 'box')
+
+ax[0].set_xticks(ticks=[-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
+ax[0].set_xticklabels(['$-\pi$', r'$-\frac{\pi}{2}$', '$0$', r'$\frac{\pi}{2}$', '$\pi$'],
+ fontsize=20)
+ax[0].set_yticks(ticks=[-2, -1, 0, 1, 2])
+ax[0].set_yticklabels(['$-2$', '$-1$', '$0$', '$1$', '$2$'],
+ fontsize=20)
+ax[0].set_xlabel('$\phi$', fontsize=24)
+ax[0].set_ylabel('$x$', fontsize=24)
+
+ax[0].set_title('Target', fontsize=24)
+
+log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[1].pcolormesh(yy, xx, prob.data.numpy(), cmap='coolwarm')
+ax[1].set_aspect('equal', 'box')
+
+ax[1].set_xticks(ticks=[-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
+ax[1].set_xticklabels(['$-\pi$', r'$-\frac{\pi}{2}$', '$0$', r'$\frac{\pi}{2}$', '$\pi$'],
+ fontsize=20)
+ax[1].set_xlabel('$\phi$', fontsize=24)
+
+ax[1].set_title('Neural Spline Flow', fontsize=24)
+
+plt.subplots_adjust(wspace=0.1)
+
+plt.show()
+# 3D plot
+fig = plt.figure(figsize=(15, 7))
+ax1 = fig.add_subplot(1, 2, 1, projection='3d')
+ax2 = fig.add_subplot(1, 2, 2, projection='3d')
+
+phi = np.linspace(-np.pi, np.pi, grid_size)
+z = np.linspace(-2.5, 2.5, grid_size)
+
+# create the surface
+x = np.outer(np.ones(grid_size), np.cos(phi))
+y = np.outer(np.ones(grid_size), np.sin(phi))
+z = np.outer(z, np.ones(grid_size))
+
+# Target
+log_prob = target.log_prob(zz).view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+prob_vis = prob / torch.max(prob)
+myheatmap = prob_vis.data.numpy()
+
+ax1._axis3don = False
+ax1.plot_surface(x, y, z, cstride=1, rstride=1, facecolors=cm.coolwarm(myheatmap), shade=False)
+
+ax1.set_title('Target', fontsize=24, y=0.97, pad=0)
+
+# Model
+log_prob = model.log_prob(zz.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+prob_vis = prob / torch.max(prob)
+myheatmap = prob_vis.data.numpy()
+
+ax2._axis3don = False
+ax2.plot_surface(x, y, z, cstride=1, rstride=1, facecolors=cm.coolwarm(myheatmap), shade=False)
+
+t = ax2.set_title('Neural Spline Flow', fontsize=24, y=0.97, pad=0)
+
+plt.show()
+from __future__ import print_function
+import torch
+import torch.utils.data
+from torch import nn, optim
+from torch.distributions.normal import Normal
+from torch.nn import functional as F
+from torchvision import datasets, transforms
+from tqdm import tqdm
+import argparse
+from datetime import datetime
+import os
+import pandas as pd
+parser = argparse.ArgumentParser(description="FlowVAE implementation on MNIST")
+parser.add_argument(
+ "--batch-size",
+ type=int,
+ default=256,
+ metavar="N",
+ help="Training batch size (default: 256)",
+)
+parser.add_argument(
+ "--latent-size",
+ type=int,
+ default=40,
+ metavar="N",
+ help="Latent dimension size (default: 40)",
+)
+parser.add_argument(
+ "--epochs",
+ type=int,
+ default=15,
+ metavar="N",
+ help="Nr of training epochs (default: 15)",
+)
+parser.add_argument(
+ "--dataset",
+ type=str,
+ default="mnist",
+ metavar="N",
+ help="Dataset to train and test on (mnist, cifar10 or cifar100) (default: mnist)",
+)
+parser.add_argument(
+ "--no-cuda", action="store_true", default=False, help="enables CUDA training"
+)
+parser.add_argument(
+ "--seed", type=int, default=15, metavar="S", help="Random Seed (default: 1)"
+)
+parser.add_argument(
+ "--log-intv",
+ type=int,
+ default=20,
+ metavar="N",
+ help="Training log status interval (default: 20",
+)
+parser.add_argument(
+ "--experiment_mode",
+ type=bool,
+ default=False,
+ metavar="N",
+ help="Experiment mode (conducts 10 runs and saves results as DataFrame (default: False)",
+)
+parser.add_argument(
+ "--runs",
+ type=int,
+ default=10,
+ metavar="N",
+ help="Number of runs in experiment_mode (experiment_mode has to be turned to True to use) (default: 10)",
+)
+args = parser.parse_args()
+args.cuda = not args.no_cuda and torch.cuda.is_available()
+torch.manual_seed(args.seed)
+device = torch.device("cuda" if args.cuda else "cpu")
+if args.dataset == "mnist":
+ img_dim = 28
+elif args.dataset == "cifar10" or args.dataset == "cifar100":
+ img_dim = 32
+else:
+ raise ValueError("The only dataset calls supported are: mnist, cifar10, cifar100")
+class VAE(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.encode = nn.Sequential(
+ nn.Linear(img_dim**2, 512),
+ nn.ReLU(True),
+ nn.Linear(512, 256),
+ nn.ReLU(True),
+ )
+ self.f1 = nn.Linear(256, args.latent_size)
+ self.f2 = nn.Linear(256, args.latent_size)
+ self.decode = nn.Sequential(
+ nn.Linear(args.latent_size, 256),
+ nn.ReLU(True),
+ nn.Linear(256, 512),
+ nn.ReLU(True),
+ nn.Linear(512, img_dim**2),
+ )
+
+ def forward(self, x):
+ # Encode
+ mu, log_var = self.f1(
+ self.encode(x.view(x.size(0) * x.size(1), img_dim**2))
+ ), self.f2(self.encode(x.view(x.size(0) * x.size(1), img_dim**2)))
+
+ # Reparametrize variables
+ std = torch.exp(0.5 * log_var)
+ norm_scale = torch.randn_like(std)
+ z_ = mu + norm_scale * std
+
+ # Q0 and prior
+ q0 = Normal(mu, torch.exp((0.5 * log_var)))
+ p = Normal(0.0, 1.0)
+
+ # Decode
+ z_ = z_.view(z_.size(0), args.latent_size)
+ zD = self.decode(z_)
+ out = torch.sigmoid(zD)
+
+ return out, mu, log_var
+def bound(rce, x, mu, log_var):
+ kld = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
+ return F.binary_cross_entropy(rce, x.view(-1, img_dim**2), reduction="sum") + kld
+class BinaryTransform:
+ def __init__(self, thresh=0.5):
+ self.thresh = thresh
+
+ def __call__(self, x):
+ return (x > self.thresh).type(x.type())
+# Training
+def flow_vae_datasets(
+ id,
+ download=True,
+ batch_size=args.batch_size,
+ shuffle=True,
+ transform=transforms.Compose([transforms.ToTensor(), BinaryTransform()]),
+):
+ data_d_train = {
+ "mnist": datasets.MNIST(
+ "datasets", train=True, download=True, transform=transform
+ ),
+ "cifar10": datasets.CIFAR10(
+ "datasets", train=True, download=True, transform=transform
+ ),
+ "cifar100": datasets.CIFAR100(
+ "datasets", train=True, download=True, transform=transform
+ ),
+ }
+ data_d_test = {
+ "mnist": datasets.MNIST(
+ "datasets", train=False, download=True, transform=transform
+ ),
+ "cifar10": datasets.CIFAR10(
+ "datasets", train=False, download=True, transform=transform
+ ),
+ "cifar100": datasets.CIFAR100(
+ "datasets", train=False, download=True, transform=transform
+ ),
+ }
+ train_loader = torch.utils.data.DataLoader(
+ data_d_train.get(id), batch_size=batch_size, shuffle=shuffle
+ )
+
+ test_loader = torch.utils.data.DataLoader(
+ data_d_test.get(id), batch_size=batch_size, shuffle=shuffle
+ )
+ return train_loader, test_loader
+model = VAE().to(device)
+optimizer = optim.Adam(model.parameters(), lr=0.001)
+# train_losses = []
+train_loader, test_loader = flow_vae_datasets(args.dataset)
+Train
+def train(model, epoch):
+ model.train()
+ tr_loss = 0
+ progressbar = tqdm(enumerate(train_loader), total=len(train_loader))
+ for batch_n, (x, n) in progressbar:
+ x = x.to(device)
+ optimizer.zero_grad()
+ rc_batch, mu, log_var = model(x)
+ loss = bound(rc_batch, x.view(x.size(0) * x.size(1), img_dim**2), mu, log_var)
+ loss.backward()
+ tr_loss += loss.item()
+ optimizer.step()
+ progressbar.update()
+ if batch_n % args.log_intv == 0:
+ print(
+ "Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}".format(
+ epoch,
+ batch_n * len(x),
+ len(train_loader.dataset),
+ 100.0 * batch_n / len(train_loader),
+ loss.item() / len(x),
+ )
+ )
+ progressbar.close()
+ print(
+ "====> Epoch: {} Average loss: {:.4f}".format(
+ epoch, tr_loss / len(train_loader.dataset)
+ )
+ )
+def test(model, epoch):
+ model.eval()
+ test_loss = 0
+ with torch.no_grad():
+ for i, (x, _) in enumerate(test_loader):
+ x = x.to(device)
+ rc_batch, mu, log_var = model(x)
+ test_loss += bound(rc_batch, x, mu, log_var).item()
+
+ test_loss /= len(test_loader.dataset)
+ print("====> Test set loss: {:.4f}".format(test_loss))
+ return test_loss
+test_losses = []
+if __name__ == "__main__":
+ if args.experiment_mode:
+ min_test_losses = []
+ min_test_losses.append(str(args))
+ for i in range(args.runs):
+ test_losses = []
+ model.__init__()
+ model = model.to(device)
+ optimizer = optim.Adam(model.parameters(), lr=0.001)
+ if i == 0:
+ seed = args.seed
+ else:
+ seed += 1
+ torch.manual_seed(seed)
+ for e in range(args.epochs):
+ train(model, e)
+ tl = test(model, e)
+ test_losses.append(tl)
+ print("====> Lowest test set loss: {:.4f}".format(min(test_losses)))
+ min_test_losses.append(min(test_losses))
+ Series = pd.Series(min_test_losses)
+
+ dirName = "experiments"
+ if not os.path.exists(dirName):
+ os.mkdir(dirName)
+ else:
+ pass
+ file_name = dirName + "/{}.xlsx".format(str(datetime.now()))
+ file_name = file_name.replace(":", "-")
+ Series.to_excel(file_name, index=False, header=None)
+ else:
+ for e in range(args.epochs):
+ train(model, e)
+ tl = test(model, e)
+ test_losses.append(tl)
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+K = 16
+#torch.manual_seed(0)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+
+flows = []
+for i in range(K):
+ flows += [nf.flows.Planar((2,))]
+target = nf.distributions.TwoModes(2, 0.1)
+
+q0 = nf.distributions.DiagGaussian(2)
+nfm = nf.NormalizingFlow(q0=q0, flows=flows, p=target)
+nfm.to(device)
+# Plot target distribution
+grid_size = 200
+xx, yy = torch.meshgrid(torch.linspace(-3, 3, grid_size), torch.linspace(-3, 3, grid_size))
+z = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+log_prob = target.log_prob(z.to(device)).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+
+plt.figure(figsize=(10, 10))
+plt.pcolormesh(xx, yy, prob)
+plt.show()
+
+# Plot initial flow distribution
+z, _ = nfm.sample(num_samples=2 ** 20)
+z_np = z.to('cpu').data.numpy()
+plt.figure(figsize=(10, 10))
+plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (grid_size, grid_size), range=[[-3, 3], [-3, 3]])
+plt.show()
+# Train model
+max_iter = 20000
+num_samples = 2 * 20
+anneal_iter = 10000
+annealing = True
+show_iter = 2000
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-3, weight_decay=1e-4)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+ if annealing:
+ loss = nfm.reverse_kld(num_samples, beta=np.min([1., 0.01 + it / anneal_iter]))
+ else:
+ loss = nfm.reverse_kld(num_samples)
+ loss.backward()
+ optimizer.step()
+
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ torch.cuda.manual_seed(0)
+ z, _ = nfm.sample(num_samples=2 ** 20)
+ z_np = z.to('cpu').data.numpy()
+
+ plt.figure(figsize=(10, 10))
+ plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (grid_size, grid_size), range=[[-3, 3], [-3, 3]])
+ plt.show()
+
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot learned distribution
+z, _ = nfm.sample(num_samples=2 ** 20)
+z_np = z.to('cpu').data.numpy()
+plt.figure(figsize=(10, 10))
+plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (grid_size, grid_size), range=[[-3, 3], [-3, 3]])
+plt.show()
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+from tqdm import tqdm
+# Set up model
+
+# Define flows
+K = 64
+torch.manual_seed(0)
+
+latent_size = 2
+b = torch.Tensor([1 if i % 2 == 0 else 0 for i in range(latent_size)])
+flows = []
+for i in range(K):
+ s = nf.nets.MLP([latent_size, 2 * latent_size, latent_size], init_zeros=True)
+ t = nf.nets.MLP([latent_size, 2 * latent_size, latent_size], init_zeros=True)
+ if i % 2 == 0:
+ flows += [nf.flows.MaskedAffineFlow(b, t, s)]
+ else:
+ flows += [nf.flows.MaskedAffineFlow(1 - b, t, s)]
+ flows += [nf.flows.ActNorm(latent_size)]
+
+# Set target and q0
+target = nf.distributions.TwoModes(2, 0.1)
+q0 = nf.distributions.DiagGaussian(2)
+
+# Construct flow model
+nfm = nf.NormalizingFlow(q0=q0, flows=flows, p=target)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+nfm = nfm.to(device)
+nfm = nfm.double()
+
+# Initialize ActNorm
+z, _ = nfm.sample(num_samples=2 ** 7)
+z_np = z.to('cpu').data.numpy()
+plt.figure(figsize=(15, 15))
+plt.hist2d(z_np[:, 0].flatten(), z_np[:, 1].flatten(), (200, 200), range=[[-3, 3], [-3, 3]])
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Plot target distribution
+grid_size = 200
+xx, yy = torch.meshgrid(torch.linspace(-3, 3, grid_size), torch.linspace(-3, 3, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.double().to(device)
+log_prob = target.log_prob(zz).to('cpu').view(*xx.shape)
+prob_target = torch.exp(log_prob)
+
+# Plot initial posterior distribution
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.contour(xx, yy, prob_target.data.numpy(), cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 20000
+num_samples = 2 * 10
+anneal_iter = 10000
+annealing = True
+show_iter = 1000
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(nfm.parameters(), lr=1e-4, weight_decay=1e-6)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+ if annealing:
+ loss = nfm.reverse_kld(num_samples, beta=np.min([1., 0.001 + it / anneal_iter]))
+ else:
+ loss = nfm.reverse_alpha_div(num_samples, dreg=True, alpha=1)
+
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned posterior
+ if (it + 1) % show_iter == 0:
+ log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+ prob = torch.exp(log_prob)
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(xx, yy, prob.data.numpy())
+ plt.contour(xx, yy, prob_target.data.numpy(), cmap=plt.get_cmap('cool'), linewidths=2)
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot learned posterior distribution
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.contour(xx, yy, prob_target.data.numpy(), cmap=plt.get_cmap('cool'), linewidths=2)
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+This notebook illustrates how to use the normflows packages by training a simple Real NVP model to a 2D distribution consisting on two half moons.
Before we can start, we have to install the package.
+!pip install normflows
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from matplotlib import pyplot as plt
+
+from tqdm import tqdm
+After importing the required packages, we want to create a nf.NormalizingFlow model. Therefore, we need a base distribution, which we set to be a Gaussian, and a list of flow layers. The flow layers are simply affine coupling layers, whereby nf.AffineCouplingBlock already includes the splitting and merging of the features as it is done in coupling. We also swap the features after each layer to ensure that they are all modified.
# Set up model
+
+# Define 2D Gaussian base distribution
+base = nf.distributions.base.DiagGaussian(2)
+
+# Define list of flows
+num_layers = 32
+flows = []
+for i in range(num_layers):
+ # Neural network with two hidden layers having 64 units each
+ # Last layer is initialized by zeros making training more stable
+ param_map = nf.nets.MLP([1, 64, 64, 2], init_zeros=True)
+ # Add flow layer
+ flows.append(nf.flows.AffineCouplingBlock(param_map))
+ # Swap dimensions
+ flows.append(nf.flows.Permute(2, mode='swap'))
+
+# Construct flow model
+model = nf.NormalizingFlow(base, flows)
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+model = model.to(device)
+This is our target distribution.
+# Define target distribution
+target = nf.distributions.TwoMoons()
+# Plot target distribution
+grid_size = 200
+xx, yy = torch.meshgrid(torch.linspace(-3, 3, grid_size), torch.linspace(-3, 3, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.to(device)
+
+log_prob = target.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Plot initial flow distribution
+model.eval()
+log_prob = model.log_prob(zz).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+Now, we are ready to train the flow model. This can be done in a similar fashion as standard neural networks. Since we use samples from the target for training, we use the forward KL divergence as objective, which is equivalent to maximum likelihood.
+# Train model
+max_iter = 4000
+num_samples = 2 ** 9
+show_iter = 500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(model.parameters(), lr=5e-4, weight_decay=1e-5)
+
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ x = target.sample(num_samples).to(device)
+
+ # Compute loss
+ loss = model.forward_kld(x)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ model.eval()
+ log_prob = model.log_prob(zz)
+ model.train()
+ prob = torch.exp(log_prob.to('cpu').view(*xx.shape))
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+This is our trained flow model!
+Note that there might be a density filament connecting the two modes, which is due to an architectural limitation of normalizing flows, especially prominent in Real NVP. You can find out more about it in this paper.
+# Plot target distribution
+f, ax = plt.subplots(1, 2, sharey=True, figsize=(15, 7))
+
+log_prob = target.log_prob(zz).to('cpu').view(*xx.shape)
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[0].pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+
+ax[0].set_aspect('equal', 'box')
+ax[0].set_axis_off()
+ax[0].set_title('Target', fontsize=24)
+
+# Plot learned distribution
+model.eval()
+log_prob = model.log_prob(zz).to('cpu').view(*xx.shape)
+model.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+ax[1].pcolormesh(xx, yy, prob.data.numpy(), cmap='coolwarm')
+
+ax[1].set_aspect('equal', 'box')
+ax[1].set_axis_off()
+ax[1].set_title('Real NVP', fontsize=24)
+
+plt.subplots_adjust(wspace=0.1)
+
+plt.show()
+# Import required packages
+import torch
+import numpy as np
+import normflows as nf
+
+from sklearn.datasets import make_moons
+
+from matplotlib import pyplot as plt
+
+from tqdm import tqdm
+# Set up model
+
+# Define flows
+K = 16
+torch.manual_seed(0)
+
+latent_size = 2
+hidden_units = 128
+hidden_layers = 3
+
+flows = []
+for i in range(K):
+ net = nf.nets.LipschitzMLP([latent_size] + [hidden_units] * (hidden_layers - 1) + [latent_size],
+ init_zeros=True, lipschitz_const=0.9)
+ flows += [nf.flows.Residual(net, reduce_memory=True)]
+ flows += [nf.flows.ActNorm(latent_size)]
+
+# Set prior and q0
+q0 = nf.distributions.DiagGaussian(2, trainable=False)
+
+# Construct flow model
+nfm = nf.NormalizingFlow(q0=q0, flows=flows)
+
+# Move model on GPU if available
+enable_cuda = True
+device = torch.device('cuda' if torch.cuda.is_available() and enable_cuda else 'cpu')
+nfm = nfm.to(device)
+
+# Initialize ActNorm
+x_np, _ = make_moons(2 ** 9, noise=0.1)
+x = torch.tensor(x_np).float().to(device)
+_ = nfm.log_prob(x)
+# Plot target distribution
+x_np, _ = make_moons(2 ** 20, noise=0.1)
+plt.figure(figsize=(15, 15))
+plt.hist2d(x_np[:, 0], x_np[:, 1], bins=200)
+plt.show()
+
+# Plot initial flow distribution
+grid_size = 100
+xx, yy = torch.meshgrid(torch.linspace(-1.5, 2.5, grid_size), torch.linspace(-2, 2, grid_size))
+zz = torch.cat([xx.unsqueeze(2), yy.unsqueeze(2)], 2).view(-1, 2)
+zz = zz.to(device)
+
+nfm.eval()
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+nfm.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+# Train model
+max_iter = 20000
+num_samples = 2 ** 9
+show_iter = 500
+
+
+loss_hist = np.array([])
+
+optimizer = torch.optim.Adam(nfm.parameters(), lr=3e-4, weight_decay=1e-5)
+for it in tqdm(range(max_iter)):
+ optimizer.zero_grad()
+
+ # Get training samples
+ x_np, _ = make_moons(num_samples, noise=0.1)
+ x = torch.tensor(x_np).float().to(device)
+
+ # Compute loss
+ loss = nfm.forward_kld(x)
+
+ # Do backprop and optimizer step
+ if ~(torch.isnan(loss) | torch.isinf(loss)):
+ loss.backward()
+ optimizer.step()
+
+ # Make layers Lipschitz continuous
+ nf.utils.update_lipschitz(nfm, 50)
+
+ # Log loss
+ loss_hist = np.append(loss_hist, loss.to('cpu').data.numpy())
+
+ # Plot learned distribution
+ if (it + 1) % show_iter == 0:
+ nfm.eval()
+ log_prob = nfm.log_prob(zz)
+ nfm.train()
+ prob = torch.exp(log_prob.to('cpu').view(*xx.shape))
+ prob[torch.isnan(prob)] = 0
+
+ plt.figure(figsize=(15, 15))
+ plt.pcolormesh(xx, yy, prob.data.numpy())
+ plt.gca().set_aspect('equal', 'box')
+ plt.show()
+
+# Plot loss
+plt.figure(figsize=(10, 10))
+plt.plot(loss_hist, label='loss')
+plt.legend()
+plt.show()
+# Plot learned distribution
+nfm.eval()
+log_prob = nfm.log_prob(zz).to('cpu').view(*xx.shape)
+nfm.train()
+prob = torch.exp(log_prob)
+prob[torch.isnan(prob)] = 0
+
+plt.figure(figsize=(15, 15))
+plt.pcolormesh(xx, yy, prob.data.numpy())
+plt.gca().set_aspect('equal', 'box')
+plt.show()
+from __future__ import print_function
+import torch
+import torch.utils.data
+from torch import nn, optim
+from torch.distributions.normal import Normal
+from torch.nn import functional as F
+from torchvision import datasets, transforms
+from tqdm import tqdm
+from normflows.flows import Planar, Radial, MaskedAffineFlow, BatchNorm
+import argparse
+from datetime import datetime
+import os
+from normflows import nets
+import pandas as pd
+import random
+parser = argparse.ArgumentParser(description="FlowVAE implementation on MNIST")
+parser.add_argument(
+ "--batch-size",
+ type=int,
+ default=256,
+ metavar="N",
+ help="Training batch size (default: 256)",
+)
+parser.add_argument(
+ "--latent-size",
+ type=int,
+ default=40,
+ metavar="N",
+ help="Latent dimension size (default: 40)",
+)
+parser.add_argument(
+ "--K", type=int, default=10, metavar="N", help="Number of flows (default: 10)"
+)
+parser.add_argument(
+ "--flow",
+ type=str,
+ default="Planar",
+ metavar="N",
+ help="Type of flow (default: Planar)",
+)
+parser.add_argument(
+ "--epochs",
+ type=int,
+ default=15,
+ metavar="N",
+ help="Nr of training epochs (default: 15)",
+)
+parser.add_argument(
+ "--dataset",
+ type=str,
+ default="mnist",
+ metavar="N",
+ help="Dataset to train and test on (mnist, cifar10 or cifar100) (default: mnist)",
+)
+parser.add_argument(
+ "--no-cuda", action="store_true", default=False, help="enables CUDA training"
+)
+parser.add_argument(
+ "--seed", type=int, default=15, metavar="S", help="Random Seed (default: 1)"
+)
+parser.add_argument(
+ "--log-intv",
+ type=int,
+ default=20,
+ metavar="N",
+ help="Training log status interval (default: 20",
+)
+parser.add_argument(
+ "--experiment_mode",
+ type=bool,
+ default=False,
+ metavar="N",
+ help="Experiment mode (conducts 10 runs and saves results as DataFrame (default: False)",
+)
+parser.add_argument(
+ "--runs",
+ type=int,
+ default=10,
+ metavar="N",
+ help="Number of runs in experiment_mode (experiment_mode has to be turned to True to use) (default: 10)",
+)
+args = parser.parse_args()
+args.cuda = not args.no_cuda and torch.cuda.is_available()
+torch.manual_seed(args.seed)
+device = torch.device("cuda" if args.cuda else "cpu")
+class SimpleFlowModel(nn.Module):
+ def __init__(self, flows):
+ super().__init__()
+ self.flows = nn.ModuleList(flows)
+
+ def forward(self, z):
+ ld = 0.0
+ for flow in self.flows:
+ z, ld_ = flow(z)
+ ld += ld_
+
+ return z, ld
+class BinaryTransform:
+ def __init__(self, thresh=0.5):
+ self.thresh = thresh
+
+ def __call__(self, x):
+ return (x > self.thresh).type(x.type())
+class ColourNormalize:
+ def __init__(self, a=0.0, b=0.0):
+ self.a = a
+ self.b = b
+
+ def __call__(self, x):
+ return (self.b - self.a) * x / 255 + self.a
+if args.dataset == "mnist":
+ img_dim = 28
+ dtf = transforms.Compose([transforms.ToTensor(), BinaryTransform()])
+elif args.dataset == "cifar10" or args.dataset == "cifar100":
+ img_dim = 8
+ dtf = transforms.Compose(
+ [
+ transforms.RandomCrop([8, 8]),
+ transforms.ToTensor(),
+ ColourNormalize(0.0001, 1 - 0.0001),
+ ]
+ )
+else:
+ raise ValueError("The only dataset calls supported are: mnist, cifar10, cifar100")
+def extract_cifar_patch(tensor, target_size):
+ x = random.randint(0, 32 - target_size)
+ y = random.randint(0, 32 - target_size)
+ return tensor[x : x + target_size, y : y + target_size, :]
+# Training
+def flow_vae_datasets(
+ id,
+ download=True,
+ batch_size=args.batch_size,
+ shuffle=True,
+ transform=dtf,
+ patch_size=None,
+):
+ data_d_train = {
+ "mnist": datasets.MNIST(
+ "datasets", train=True, download=True, transform=transform
+ ),
+ "cifar10": datasets.CIFAR10(
+ "datasets", train=True, download=True, transform=transform
+ ),
+ "cifar100": datasets.CIFAR100(
+ "datasets", train=True, download=True, transform=transform
+ ),
+ }
+ data_d_test = {
+ "mnist": datasets.MNIST(
+ "datasets", train=False, download=True, transform=transform
+ ),
+ "cifar10": datasets.CIFAR10(
+ "datasets", train=False, download=True, transform=transform
+ ),
+ "cifar100": datasets.CIFAR100(
+ "datasets", train=False, download=True, transform=transform
+ ),
+ }
+
+ # training_data = data_d_train.get(id)
+ # test_data = data_d_test.get(id)
+ # if patch_size is not None:
+ # training_data.data = np.stack(
+ # [extract_cifar_patch(training_data.data[i, :, :], patch_size) for i in range(len(training_data.data))])
+ # test_data.data = np.stack(
+ # [extract_cifar_patch(test_data.data[i, :, :], patch_size) for i in range(len(test_data.data))])
+
+ train_loader = torch.utils.data.DataLoader(
+ data_d_train.get(id), batch_size=batch_size, shuffle=shuffle
+ )
+
+ test_loader = torch.utils.data.DataLoader(
+ data_d_test.get(id), batch_size=batch_size, shuffle=shuffle
+ )
+ return train_loader, test_loader
+class FlowVAE(nn.Module):
+ def __init__(self, flows):
+ super().__init__()
+ self.encode = nn.Sequential(
+ nn.Linear(img_dim**2, 512),
+ nn.ReLU(True),
+ nn.Linear(512, 256),
+ nn.ReLU(True),
+ )
+ self.f1 = nn.Linear(256, args.latent_size)
+ self.f2 = nn.Linear(256, args.latent_size)
+ self.decode = nn.Sequential(
+ nn.Linear(args.latent_size, 256),
+ nn.ReLU(True),
+ nn.Linear(256, 512),
+ nn.ReLU(True),
+ nn.Linear(512, img_dim**2),
+ )
+ self.flows = flows
+
+ def forward(self, x):
+ # Encode
+ mu, log_var = self.f1(
+ self.encode(x.view(x.size(0) * x.size(1), img_dim**2))
+ ), self.f2(self.encode(x.view(x.size(0) * x.size(1), img_dim**2)))
+
+ # Reparameterize variables
+ std = torch.exp(0.5 * log_var)
+ norm_scale = torch.randn_like(std)
+ z_0 = mu + norm_scale * std
+
+ # Flow transforms
+ z_, log_det = self.flows(z_0)
+ z_ = z_.squeeze()
+
+ # Q0 and prior
+ q0 = Normal(mu, torch.exp((0.5 * log_var)))
+ p = Normal(0.0, 1.0)
+
+ # KLD including logdet term
+ kld = (
+ -torch.sum(p.log_prob(z_), -1)
+ + torch.sum(q0.log_prob(z_0), -1)
+ - log_det.view(-1)
+ )
+ self.test_params = [
+ torch.mean(-torch.sum(p.log_prob(z_), -1)),
+ torch.mean(torch.sum(q0.log_prob(z_0), -1)),
+ torch.mean(log_det.view(-1)),
+ torch.mean(kld),
+ ]
+
+ # Decode
+ z_ = z_.view(z_.size(0), args.latent_size)
+ zD = self.decode(z_)
+ out = torch.sigmoid(zD)
+
+ return out, kld
+def logit(x):
+ return torch.log(x / (1 - x))
+def bound(rce, x, kld, beta):
+ if args.dataset == "mnist":
+ return (
+ F.binary_cross_entropy(rce, x.view(-1, img_dim**2), reduction="sum")
+ + beta * kld
+ )
+ elif args.dataset == "cifar10" or args.dataset == "cifar100":
+ # return (- torch.distributions.Normal(x.view(-1, img_dim ** 2), 1.).log_prob(rce)).sum() + beta * kld
+ return F.mse_loss(rce, x, reduction="sum") + beta * kld
+if args.flow == "Planar":
+ flows = SimpleFlowModel([Planar((args.latent_size,)) for k in range(args.K)])
+elif args.flow == "Radial":
+ flows = SimpleFlowModel([Radial((args.latent_size,)) for k in range(args.K)])
+elif args.flow == "RealNVP":
+ b = torch.Tensor([1 if i % 2 == 0 else 0 for i in range(args.latent_size)])
+ flows = []
+ for i in range(args.K):
+ s = nets.MLP([args.latent_size, 8, args.latent_size])
+ t = nets.MLP([args.latent_size, 8, args.latent_size])
+ if i % 2 == 0:
+ flows += [MaskedAffineFlow(b, t, s)]
+ else:
+ flows += [MaskedAffineFlow(1 - b, t, s), BatchNorm()]
+ flows = SimpleFlowModel(
+ flows[:-1]
+ ) # Remove last Batch Norm layer to allow arbitrary output
+model = FlowVAE(flows).to(device)
+optimizer = optim.Adam(model.parameters(), lr=0.001)
+# train_losses = []
+train_loader, test_loader = flow_vae_datasets(args.dataset)
+def train(model, epoch, beta):
+ model.train()
+ tr_loss = 0
+ progressbar = tqdm(enumerate(train_loader), total=len(train_loader))
+ for batch_n, (x, n) in progressbar:
+ x = x.to(device)
+ optimizer.zero_grad()
+ rc_batch, kld = model(x)
+ loss = bound(
+ rc_batch, x.view(x.size(0) * x.size(1), img_dim**2), kld.sum(), beta=beta
+ )
+ avg_loss = loss / len(x)
+ loss.backward()
+ tr_loss += loss.item()
+ optimizer.step()
+ progressbar.update()
+ if batch_n % args.log_intv == 0:
+ print(
+ "Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}".format(
+ epoch,
+ batch_n * len(x),
+ len(train_loader.dataset),
+ 100.0 * batch_n / len(train_loader),
+ loss.item() / len(x),
+ )
+ )
+ print(model.test_params)
+ progressbar.close()
+ print(
+ "====> Epoch: {} Average loss: {:.4f}".format(
+ epoch, tr_loss / len(train_loader.dataset)
+ )
+ )
+def test(model, epoch):
+ model.eval()
+ test_loss = 0
+ with torch.no_grad():
+ for i, (x, _) in enumerate(test_loader):
+ x = x.to(device)
+ rc_batch, kld = model(x)
+ test_loss += bound(
+ rc_batch, x.view(x.size(0) * x.size(1), img_dim**2), kld.sum(), beta=1
+ ).item()
+
+ test_loss /= len(test_loader.dataset)
+ print("====> Test set loss: {:.4f}".format(test_loss))
+ return test_loss
+test_losses = []
+def anneal(epoch, len_e):
+ return min(1.0, 0.01 + epoch / len_e)
+if __name__ == "__main__":
+ if args.experiment_mode:
+ min_test_losses = []
+ min_test_losses.append(str(args))
+ for i in range(args.runs):
+ test_losses = []
+ model.__init__(flows)
+ model = model.to(device)
+ optimizer = optim.Adam(model.parameters(), lr=0.001)
+ if i == 0:
+ seed = args.seed
+ else:
+ seed += 1
+ torch.manual_seed(seed)
+ for e in [i + 1 for i in range(args.epochs)]:
+ beta = anneal(e, args.epochs)
+ train(model, e, beta)
+ tl = test(model, e)
+ test_losses.append(tl)
+ print("====> Lowest test set loss: {:.4f}".format(min(test_losses)))
+ min_test_losses.append(min(test_losses))
+ Series = pd.Series(min_test_losses)
+
+ dirName = "experiments"
+ if not os.path.exists(dirName):
+ os.mkdir(dirName)
+ else:
+ pass
+ file_name = dirName + "/{}.xlsx".format(str(datetime.now()))
+ file_name = file_name.replace(":", "-")
+ Series.to_excel(file_name, index=False, header=None)
+ else:
+ for e in [i + 1 for i in range(args.epochs)]:
+ beta = anneal(e, args.epochs)
+ train(model, e, beta=beta)
+ tl = test(model, e)
+ test_losses.append(tl)
+normflows: A PyTorch Package for Normalizing Flowsnormflows is a PyTorch implementation of discrete normalizing flows. Many popular flow architectures are implemented,
+see the list below. The package can be easily installed via pip.
+The basic usage is described here, and a full documentation
+is available as well. A more detailed description of this package is given in our
+accompanying paper.
Several sample use cases are provided in the
+examples folder,
+including Glow,
+a VAE, and
+a Residual Flow.
+Moreover, two simple applications are highlighed in the examples section. You can run them
+yourself in Google Colab using the links below to get a feeling for normflows.
| Architecture | +Reference | +
|---|---|
| Planar Flow | +Rezende & Mohamed, 2015 | +
| Radial Flow | +Rezende & Mohamed, 2015 | +
| NICE | +Dinh et al., 2014 | +
| Real NVP | +Dinh et al., 2017 | +
| Glow | +Kingma et al., 2018 | +
| Masked Autoregressive Flow | +Papamakarios et al., 2017 | +
| Neural Spline Flow | +Durkan et al., 2019 | +
| Circular Neural Spline Flow | +Rezende et al., 2020 | +
| Residual Flow | +Chen et al., 2019 | +
| Stochastic Normalizing Flow | +Wu et al., 2020 | +
Note that Neural Spline Flows with circular and non-circular coordinates +are supported as well.
+The latest version of the package can be installed via pip
+pip install normflows
+At least Python 3.7 is required. If you want to use a GPU, make sure that +PyTorch is set up correctly by following the instructions at the +PyTorch website.
+To run the example notebooks clone the repository first
+git clone https://github.com/VincentStimper/normalizing-flows.git
+and then install the dependencies.
+pip install -r requirements_examples.txt
+A normalizing flow consists of a base distribution, defined in
+nf.distributions.base,
+and a list of flows, given in
+nf.flows.
+Let's assume our target is a 2D distribution. We pick a diagonal Gaussian
+base distribution, which is the most popular choice. Our flow shall be a
+Real NVP model and, therefore, we need
+to define a neural network for computing the parameters of the affine coupling
+map. One dimension is used to compute the scale and shift parameter for the
+other dimension. After each coupling layer we swap their roles.
import normflows as nf
+
+# Define 2D Gaussian base distribution
+base = nf.distributions.base.DiagGaussian(2)
+
+# Define list of flows
+num_layers = 32
+flows = []
+for i in range(num_layers):
+ # Neural network with two hidden layers having 64 units each
+ # Last layer is initialized by zeros making training more stable
+ param_map = nf.nets.MLP([1, 64, 64, 2], init_zeros=True)
+ # Add flow layer
+ flows.append(nf.flows.AffineCouplingBlock(param_map))
+ # Swap dimensions
+ flows.append(nf.flows.Permute(2, mode='swap'))
+Once they are set up, we can define a
+nf.NormalizingFlow
+model. If the target density is available, it can be added to the model
+to be used during training. Sample target distributions are given in
+nf.distributions.target.
# If the target density is not given
+model = nf.NormalizingFlow(base, flows)
+
+# If the target density is given
+target = nf.distributions.target.TwoMoons()
+model = nf.NormalizingFlow(base, flows, target)
+The loss can be computed with the methods of the model and minimized.
+# When doing maximum likelihood learning, i.e. minimizing the forward KLD
+# with no target distribution given
+loss = model.forward_kld(x)
+
+# When minimizing the reverse KLD based on the given target distribution
+loss = model.reverse_kld(num_samples=512)
+
+# Optimization as usual
+loss.backward()
+optimizer.step()
+We provide several illustrative examples of how to use the package in the
+examples
+directory. Among them are implementations of
+Glow,
+a VAE, and
+a Residual Flow.
+More advanced experiments can be done with the scripts listed in the
+repository about resampled base distributions,
+see its experiments
+folder.
Below, we consider two simple 2D examples.
+In this notebook, +which can directly be opened in +Colab, +we consider a 2D distribution with two half-moon-shaped modes as a target. We approximate it with a Real NVP model +and obtain the following results.
+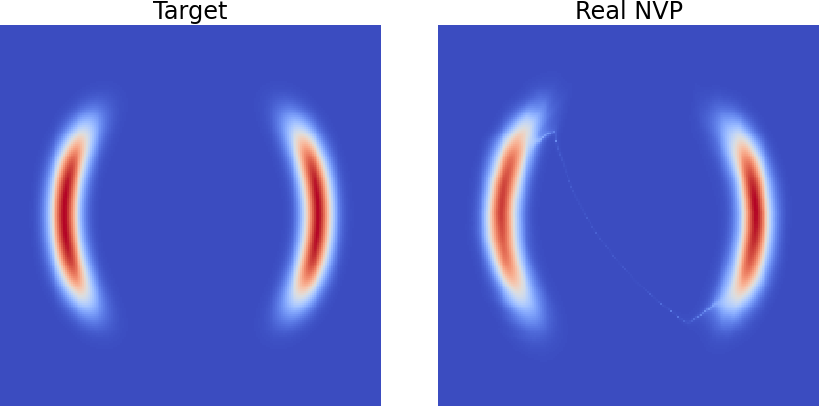
Note that there might be a density filament connecting the two modes, which is due to an architectural limitation +of normalizing flows, especially prominent in Real NVP. You can find out more about it in +this paper.
+In another example, +which is available in Colab +as well, we apply a Neural Spline Flow model to a distribution defined on a cylinder. The resulting density is visualized below.
+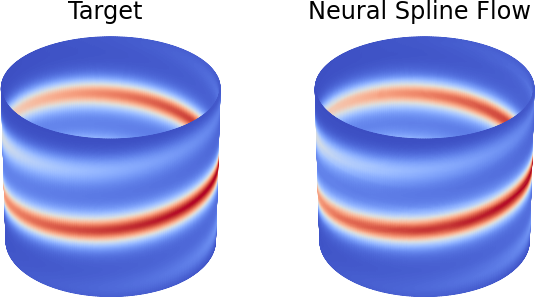
This example is considered in the paper accompanying this repository.
+If you have problems, please read the package documentation +and check out the examples section above. You are also welcome to +create issues on GitHub to get help. Note that it is +worthwhile browsing the existing open +and closed issues, which might +address the problem you are facing.
+If you find a bug or have a feature request, please +file an issue on GitHub.
+You are welcome to contribute to the package by fixing the bug or adding the feature yourself. If you want to
+contribute, please add tests for the code you added or modified and ensure it passes successfully by running pytest.
+This can be done by simply executing
pytest
+within your local version of the repository. Make sure you code is well documented, and we also encourage contributions +to the existing documentation. Once you finished coding and testing, please +create a pull request on GitHub.
+The package has been used in several research papers. Some of them are listed below.
+++Andrew Campbell, Wenlong Chen, Vincent Stimper, José Miguel Hernández-Lobato, and Yichuan Zhang. +A gradient based strategy for Hamiltonian Monte Carlo hyperparameter optimization. +In Proceedings of the 38th International Conference on Machine Learning, pp. 1238–1248. PMLR, 2021.
+ +Vincent Stimper, Bernhard Schölkopf, and José Miguel Hernández-Lobato. +Resampling Base Distributions of Normalizing Flows. +In Proceedings of The 25th International Conference on Artificial Intelligence and Statistics, volume 151, pp. 4915–4936, 2022.
+ +Laurence I. Midgley, Vincent Stimper, Gregor N. C. Simm, Bernhard Schölkopf, and José Miguel Hernández-Lobato. +Flow Annealed Importance Sampling Bootstrap. +The Eleventh International Conference on Learning Representations, 2023.
+ +Arnau Quera-Bofarull, Joel Dyer, Anisoara Calinescu, J. Doyne Farmer, and Michael Wooldridge. +BlackBIRDS: Black-Box Inference foR Differentiable Simulators. +Journal of Open Source Software, 8(89), 5776, 2023.
+ +Utkarsh Singhal, Carlos Esteves, Ameesh Makadia, and Stella X. Yu. +Learning to Transform for Generalizable Instance-wise Invariance. +Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), pp. 6211-6221, 2023.
+ +Ba-Hien Tran, Giulio Franzese, Pietro Michiardi, and Maurizio Filippone. +One-Line-of-Code Data Mollification Improves Optimization of Likelihood-based Generative Models. + Advances in Neural Information Processing Systems 36, pp. 6545–6567, 2023.
+ +
Moreover, the boltzgen package
+has been build upon normflows.
If you use normflows, please cite the
+corresponding paper as follows.
++Stimper et al., (2023). normflows: A PyTorch Package for Normalizing Flows. +Journal of Open Source Software, 8(86), 5361, https://doi.org/10.21105/joss.05361
+
Bibtex
+@article{Stimper2023,
+ author = {Vincent Stimper and David Liu and Andrew Campbell and Vincent Berenz and Lukas Ryll and Bernhard Schölkopf and José Miguel Hernández-Lobato},
+ title = {normflows: A PyTorch Package for Normalizing Flows},
+ journal = {Journal of Open Source Software},
+ volume = {8},
+ number = {86},
+ pages = {5361},
+ publisher = {The Open Journal},
+ doi = {10.21105/joss.05361},
+ url = {https://doi.org/10.21105/joss.05361},
+ year = {2023}
+}
+