1972 年由鲁道夫·贝尔提出
红黑树是平衡树的一种,在插入和删除都能在 O(lgn) 时间能完成。
红黑树能保持平衡的原因在于5条性质,红黑树必须维护这 5 条性质。
- 每一个节点不是红色就是黑色
- 根节点是黑色
- 红色节点的两个子节点为黑色
- 叶节点的 left, right 项指向一个黑色的 null 节点
- 任意一个节点,该节点到其后代所有叶子节点经过的黑色节点个数相等
红黑树插入节点与普通二叉树插入无太大区别,
因为每个节点必须有颜色,所以该插入节点必须设置一个颜色,
设置为红色比较好,因为设置为黑色,必定破坏性质 5,但设置为红色,可能破环性质 2,(排斥或)或一半可能破环性质 3.
由于当前插入的节点为红色,所以可能会违反性质 2 或(排斥或)性质 3
违反性质 2 的修正只需将根节点置为黑色即可。
违反性质 3 的修正可以细分为 6 种情况,实际上只需讨论三种情况,
因为另外三种情况为对称情况。
推论:违反性质 3 即可以推出当前节点为红色,其父节点也为红色。
假设:父节点的兄弟节点简称叔节点,父节点的父节点简称爷节点
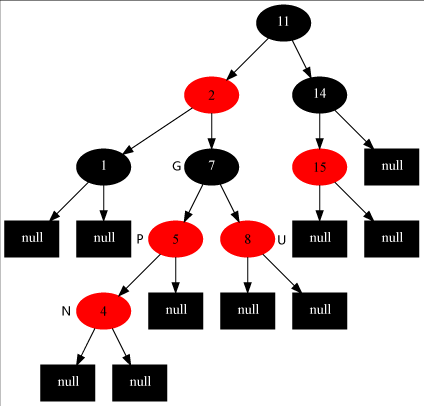
- 当叔节点为红色时,修正办法:父节点和叔节点置为黑色,爷节点置为红色;将当前节点指向爷节点,继续判读爷节点的父节点是否为红色。
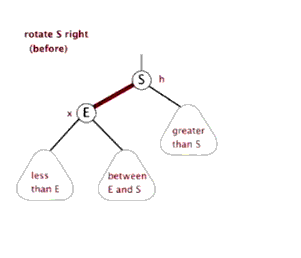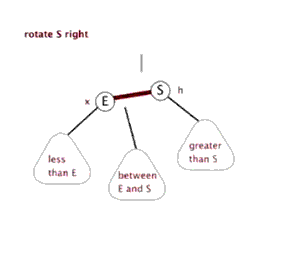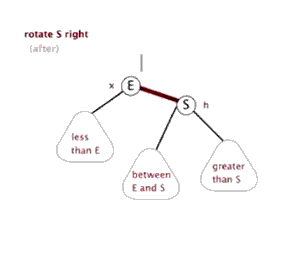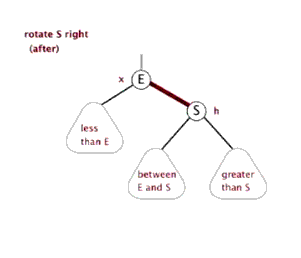
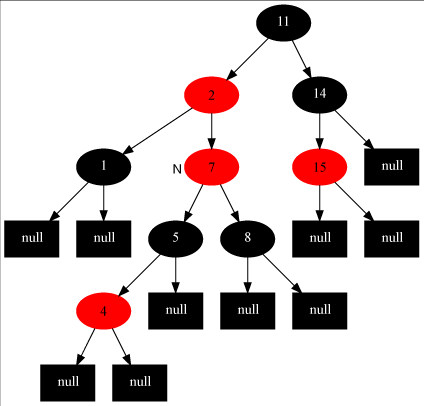
- 当叔节点为黑色,且当前节点为父节点的右孩子,修正办法:当前节点指向父节点,左旋当前节点。
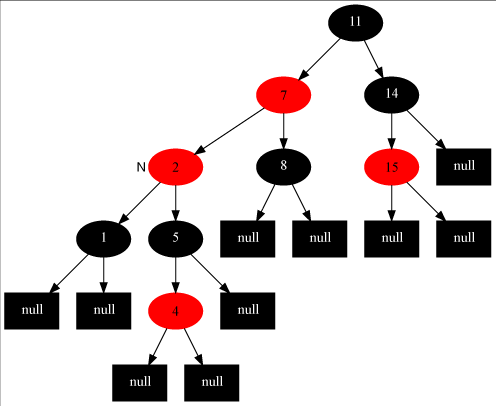
- 当叔节点为黑色,且当前节点为父节点的左孩子,修正办法:将父节点置为黑色,爷节点置为红色,右旋爷节点。
6种情况来源:父节点为爷节点的左节点有这三种情况,父节点为爷节点的右节点又有这三种情况。
两个三种情况的区别:上三种情况为父节点为爷节点的左节点时所做的操作,当父节点为爷节点的右节点时,因为对称性,情况2的左旋变为右旋,情况 3 的右旋变为左旋
从上图可以看出情况1可能转化为情况2,
情况2一定转化为情况3.
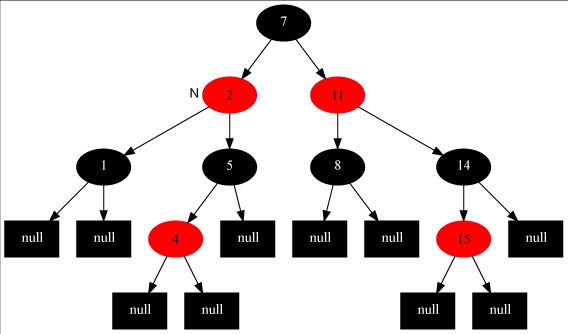
一旦执行情况2或3,即意味着树的修正结束
而情况1上升树的高度为2,
所以可以推出插入操作在O(lgn)时间内完成。
名单按照字母顺序排序。
- v1.0 2018/06/01 初稿(红黑树的插入,不含代码)