| title | thumbnail | authors | |||||
|---|---|---|---|---|---|---|---|
Guiding Text Generation with Constrained Beam Search in 🤗 Transformers |
/blog/assets/53_constrained_beam_search/thumbnail.png |
|
This blog post assumes that the reader is familiar with text generation methods using the different variants of beam search, as explained in the blog post: "How to generate text: using different decoding methods for language generation with Transformers"
Unlike ordinary beam search, constrained beam search allows us to exert control over the output of text generation. This is useful because we sometimes know exactly what we want inside the output. For example, in a Neural Machine Translation task, we might know which words must be included in the final translation with a dictionary lookup. Sometimes, generation outputs that are almost equally possible to a language model might not be equally desirable for the end-user due to the particular context. Both of these situations could be solved by allowing the users to tell the model which words must be included in the end output.
However, this is actually a very non-trivial problem. This is because the task requires us to force the generation of certain subsequences somewhere in the final output, at some point during the generation.
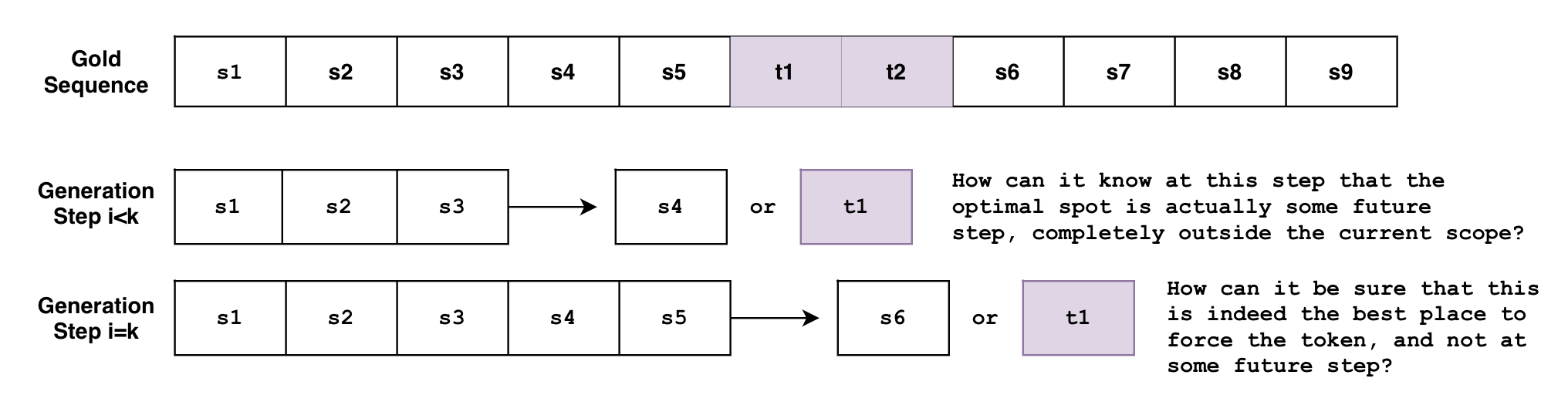
Let's say that we're want to generate a sentence S that has to include the phrase \( p_1={ t_1, t_2 } \) with tokens \( t_1, t_2 \) in order. Let's define the expected sentence \( S \) as:
The problem is that beam search generates the sequence token-by-token. Though not entirely accurate, one can think of beam search as the function \( B(\mathbf{s}{0:i}) = s{i+1} \), where it looks at the currently generated sequence of tokens from \( 0 \) to \( i \) then predicts the next token at \( i+1 \) . But how can this function know, at an arbitrary step \( i < k \) , that the tokens must be generated at some future step \( k \) ? Or when it's at the step \( i=k \) , how can it know for sure that this is the best spot to force the tokens, instead of some future step \( i>k \) ?
And what if you have multiple constraints with varying requirements? What if you want to force the phrase \( p_1={t_1, t_2} \) and also the phrase \( p_2={ t_3, t_4, t_5, t_6} \) ? What if you want the model to choose between the two phrases? What if we want to force the phrase \( p_1 \) and force just one phrase among the list of phrases \( {p_{21}, p_{22}, p_{23}} \) ?
The above examples are actually very reasonable use-cases, as it will be shown below, and the new constrained beam search feature allows for all of them!
This post will quickly go over what the new constrained beam search feature can do for you and then go into deeper details about how it works under the hood.
Let's say we're trying to translate "How old are you?" to German.
"Wie alt bist du?" is what you'd say in an informal setting, and "Wie alt sind Sie?" is what
you'd say in a formal setting.
And depending on the context, we might want one form of formality over the other, but how do we tell the model that?
Here's how we would do text translation in the traditional beam search setting.
!pip install -q git+https://github.com/huggingface/transformers.git
from transformers import AutoTokenizer, AutoModelForSeq2SeqLM
tokenizer = AutoTokenizer.from_pretrained("t5-base")
model = AutoModelForSeq2SeqLM.from_pretrained("t5-base")
encoder_input_str = "translate English to German: How old are you?"
input_ids = tokenizer(encoder_input_str, return_tensors="pt").input_ids
outputs = model.generate(
input_ids,
num_beams=10,
num_return_sequences=1,
no_repeat_ngram_size=1,
remove_invalid_values=True,
)
print("Output:\n" + 100 * '-')
print(tokenizer.decode(outputs[0], skip_special_tokens=True))Output:
----------------------------------------------------------------------------------------------------
Wie alt bist du?
But what if we knew that we wanted a formal output instead of the informal one? What if we knew from prior knowledge what the generation must include, and we could inject it into the generation?
The following is what is possible now with the force_words_ids keyword argument to model.generate():
tokenizer = AutoTokenizer.from_pretrained("t5-base")
model = AutoModelForSeq2SeqLM.from_pretrained("t5-base")
encoder_input_str = "translate English to German: How old are you?"
force_words = ["Sie"]
input_ids = tokenizer(encoder_input_str, return_tensors="pt").input_ids
force_words_ids = tokenizer(force_words, add_special_tokens=False).input_ids
outputs = model.generate(
input_ids,
force_words_ids=force_words_ids,
num_beams=5,
num_return_sequences=1,
no_repeat_ngram_size=1,
remove_invalid_values=True,
)
print("Output:\n" + 100 * '-')
print(tokenizer.decode(outputs[0], skip_special_tokens=True))Output:
----------------------------------------------------------------------------------------------------
Wie alt sind Sie?
As you can see, we were able to guide the generation with prior knowledge about our desired output. Previously we would've had to generate a bunch of possible outputs, then filter the ones that fit our requirement. Now we can do that at the generation stage.
We mentioned above a use-case where we know which words we want to be included in the final output. An example of this might be using a dictionary lookup during neural machine translation.
But what if we don't know which word forms to use, where we'd want outputs like ["raining", "rained", "rains", ...] to be equally possible? In a more general sense, there are always cases when we don't want the exact word verbatim, letter by letter, and might be open to other related possibilities too.
Constraints that allow for this behavior are Disjunctive Constraints, which allow the user to input a list of words, whose purpose is to guide the generation such that the final output must contain just at least one among the list of words.
Here's an example that uses a mix of the above two types of constraints:
from transformers import GPT2LMHeadModel, GPT2Tokenizer
model = GPT2LMHeadModel.from_pretrained("gpt2")
tokenizer = GPT2Tokenizer.from_pretrained("gpt2")
force_word = "scared"
force_flexible = ["scream", "screams", "screaming", "screamed"]
force_words_ids = [
tokenizer([force_word], add_prefix_space=True, add_special_tokens=False).input_ids,
tokenizer(force_flexible, add_prefix_space=True, add_special_tokens=False).input_ids,
]
starting_text = ["The soldiers", "The child"]
input_ids = tokenizer(starting_text, return_tensors="pt").input_ids
outputs = model.generate(
input_ids,
force_words_ids=force_words_ids,
num_beams=10,
num_return_sequences=1,
no_repeat_ngram_size=1,
remove_invalid_values=True,
)
print("Output:\n" + 100 * '-')
print(tokenizer.decode(outputs[0], skip_special_tokens=True))
print(tokenizer.decode(outputs[1], skip_special_tokens=True))Setting `pad_token_id` to `eos_token_id`:50256 for open-end generation.
Output:
----------------------------------------------------------------------------------------------------
The soldiers, who were all scared and screaming at each other as they tried to get out of the
The child was taken to a local hospital where she screamed and scared for her life, police said.
As you can see, the first output used "screaming", the second output used "screamed", and both used "scared" verbatim. The list to choose from ["screaming", "screamed", ...] doesn't have to be word forms; this can satisfy any use-case where we need just one from a list of words.
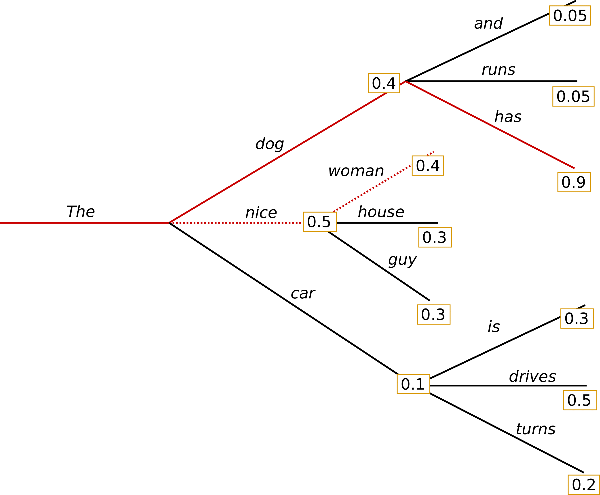
The following is an example of traditional beam search, taken from a previous blog post:
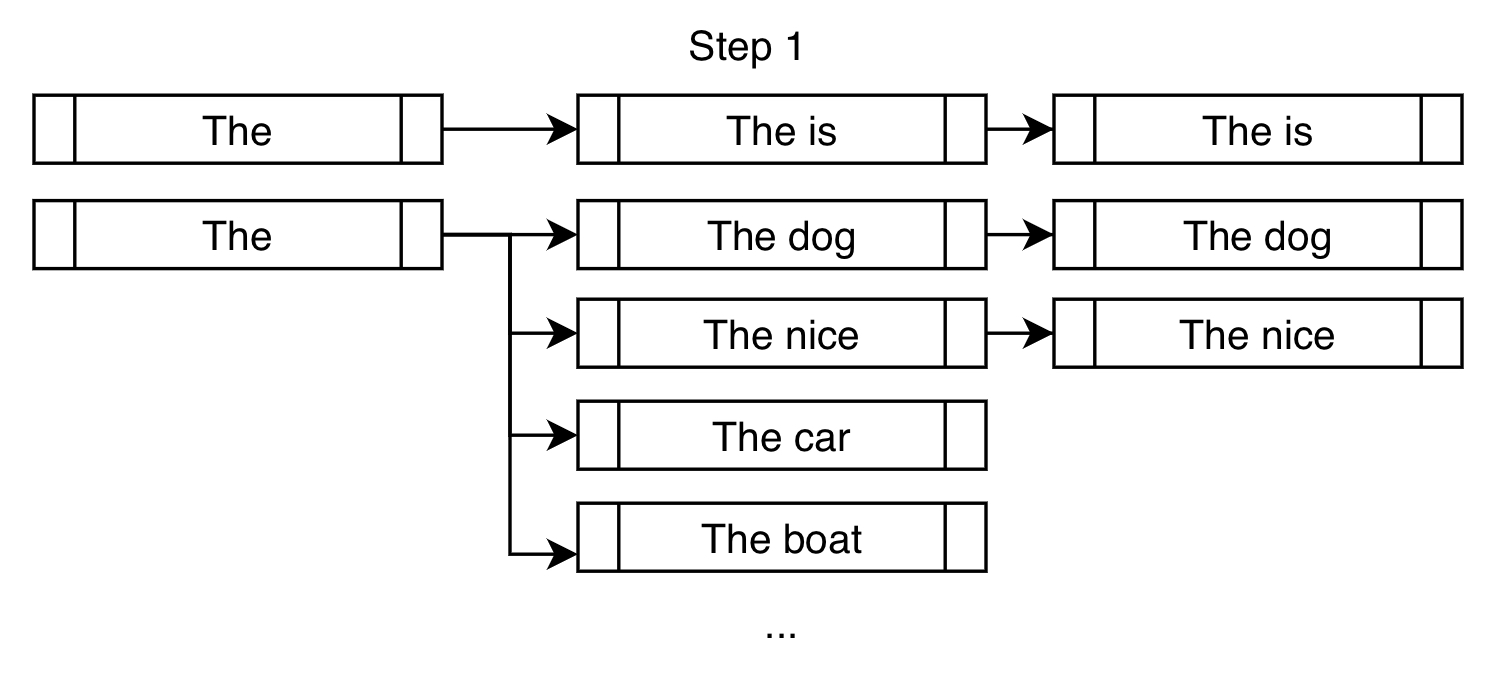
Unlike greedy search, beam search works by keeping a longer list of hypotheses. In the above picture, we have displayed three next possible tokens at each possible step in the generation.
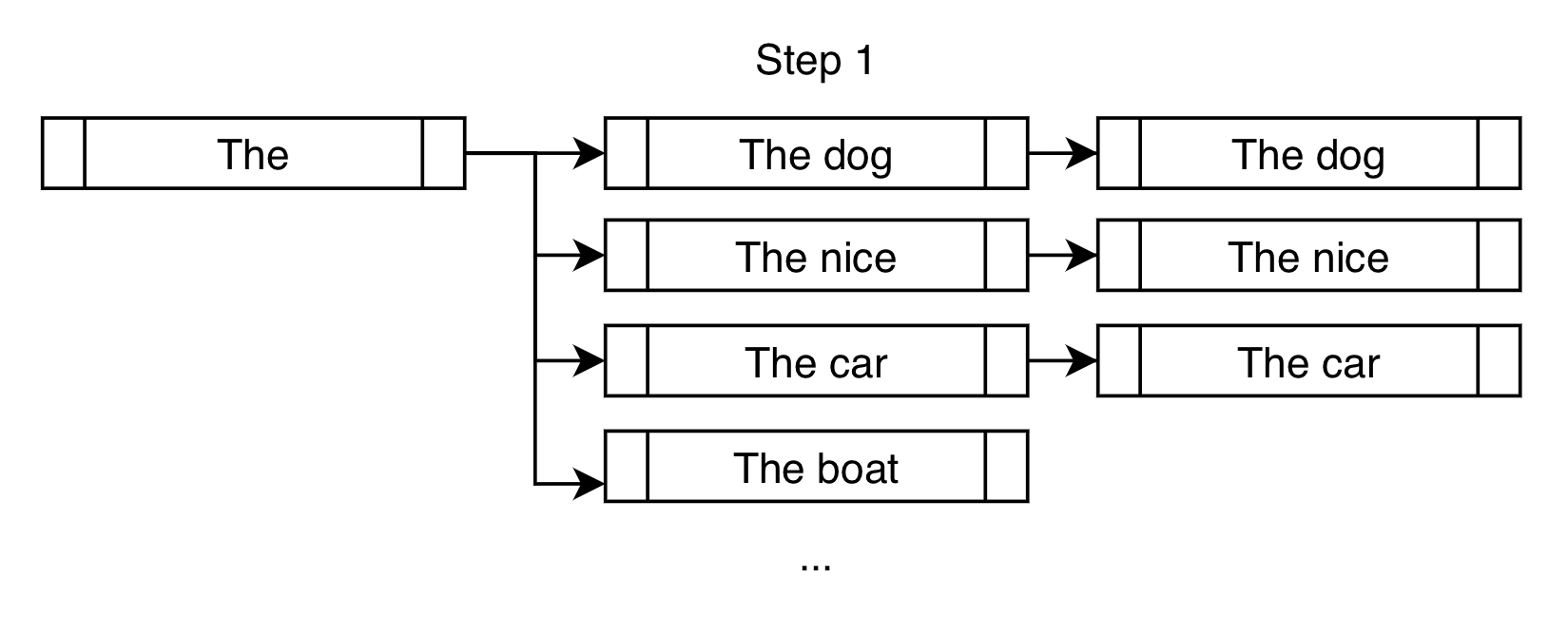
Here's another way to look at the first step of the beam search for the above example, in the case of num_beams=3:
Instead of only choosing "The dog" like what a greedy search would do, a beam search would allow further consideration of "The nice" and "The car".
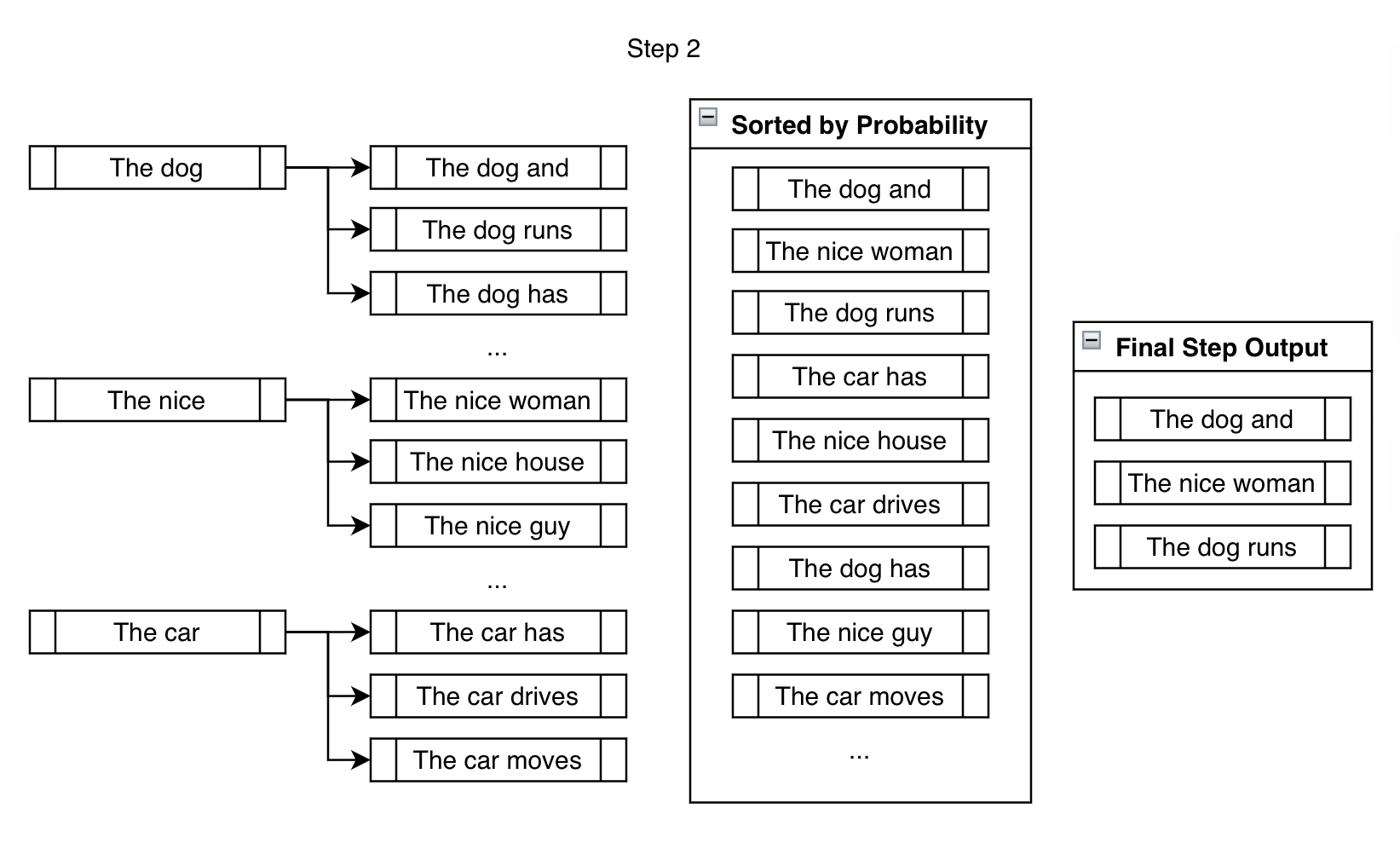
In the next step, we consider the next possible tokens for each of the three branches we created in the previous step.
Though we end up considering significantly more than num_beams outputs, we reduce them down to num_beams at the end of the step. We can't just keep branching out, then the number of beams we'd have to keep track of would be \( \text{beams}^{n} \) for \( n \) steps, which becomes very large very quickly ( \( 10 \) beams after \( 10 \) steps is \( 10,000,000,000 \) beams!).
For the rest of the generation, we repeat the above step until the ending criteria has been met, like generating the <eos> token or reaching max_length, for example. Branch out, rank, reduce, and repeat.
Constrained beam search attempts to fulfill the constraints by injecting the desired tokens at every step of the generation.
Let's say that we're trying to force the phrase "is fast" in the generated output.
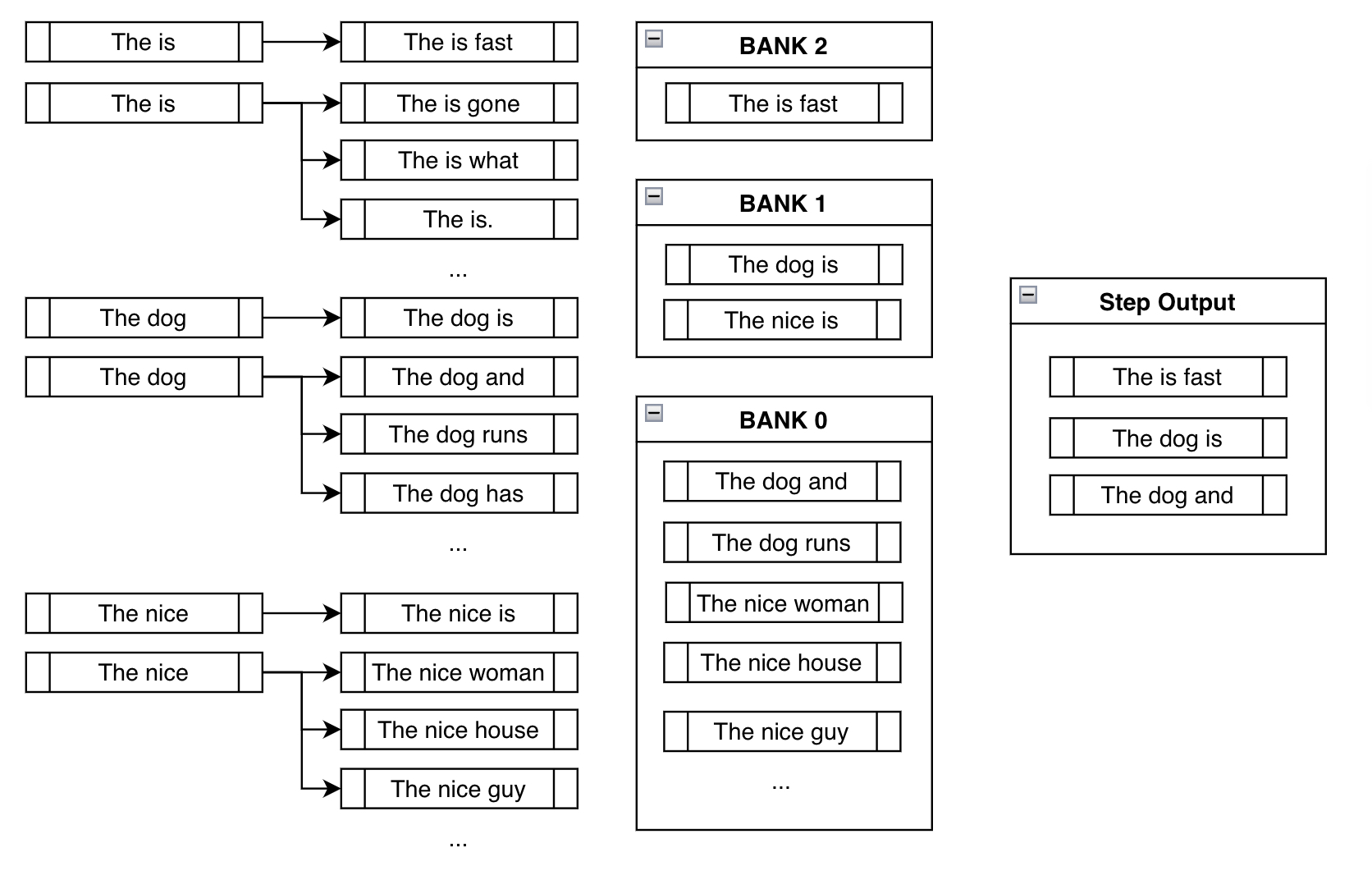
In the traditional beam search setting, we find the top k most probable next tokens at each branch and append them for consideration. In the constrained setting, we do the same but also append the tokens that will take us closer to fulfilling our constraints. Here's a demonstration:
On top of the usual high-probability next tokens like "dog" and "nice", we force the token "is" in order to get us closer to fulfilling our constraint of "is fast".
For the next step, the branched-out candidates below are mostly the same as that of traditional beam search. But like the above example, constrained beam search adds onto the existing candidates by forcing the constraints at each new branch:
Before we talk about the next step, we need to think about the resulting undesirable behavior we can see in the above step.
The problem with naively just forcing the desired phrase "is fast" in the output is that, most of the time, you'd end up with nonsensical outputs like "The is fast" above. This is actually what makes this a nontrivial problem to solve. A deeper discussion about the complexities of solving this problem can be found in the original feature request issue that was raised in huggingface/transformers.
Banks solve this problem by creating a balance between fulfilling the constraints and creating sensible output.
Bank \( n \) refers to the list of beams that have made \( n \) steps progress in fulfilling the constraints. After sorting all the possible beams into their respective banks, we do a round-robin selection. With the above example, we'd select the most probable output from Bank 2, then most probable from Bank 1, one from Bank 0, the second most probable from Bank 2, the second most probable from Bank 1, and so forth. Since we're using num_beams=3, we just do the above process three times to end up with ["The is fast", "The dog is", "The dog and"].
This way, even though we're forcing the model to consider the branch where we've manually appended the desired token, we still keep track of other high-probable sequences that probably make more sense. Even though "The is fast" fulfills our constraint completely, it's not a very sensible phrase. Luckily, we have "The dog is" and "The dog and" to work with in future steps, which hopefully will lead to more sensible outputs later on.
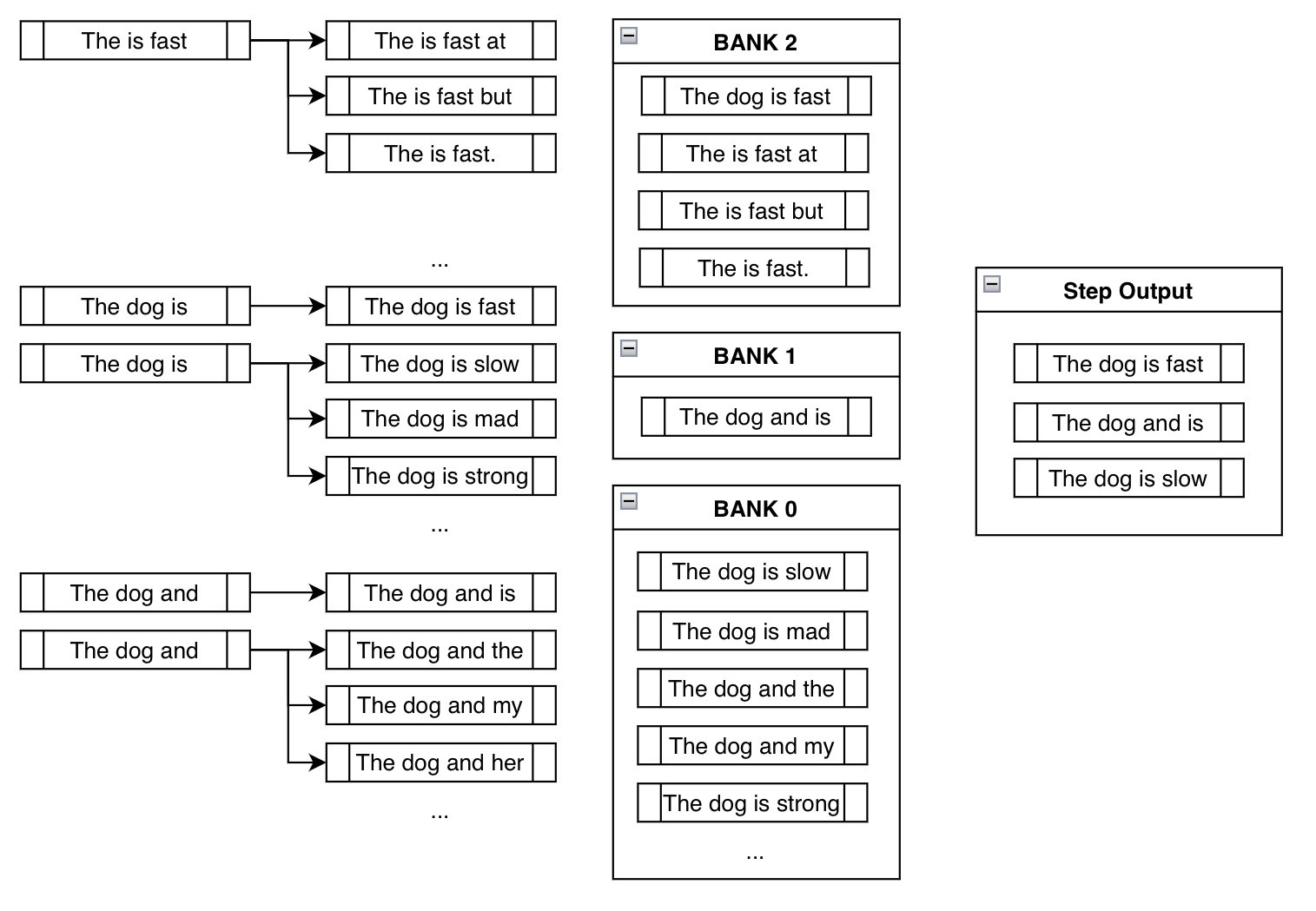
This behavior is demonstrated in the third step of the above example:
Notice how "The is fast" doesn't require any manual appending of constraint tokens since it's already fulfilled (i.e., already contains the phrase "is fast"). Also, notice how beams like "The dog is slow" or "The dog is mad" are actually in Bank 0, since, although it includes the token "is", it must restart from the beginning to generate "is fast". By appending something like "slow" after "is", it has effectively reset its progress.
And finally notice how we ended up at a sensible output that contains our constraint phrase: "The dog is fast"!
We were worried initially because blindly appending the desired tokens led to nonsensical phrases like "The is fast". However, using round-robin selection from banks, we implicitly ended up getting rid of nonsensical outputs in preference for the more sensible outputs.
The main takeaway from the explanation can be summarized as the following. At every step, we keep pestering the model to consider the tokens that fulfill our constraints, all the while keeping track of beams that don't, until we end up with reasonably high probability sequences that contain our desired phrases.
So a principled way to design this implementation was to represent each constraint as a Constraint object, whose purpose was to keep track of its progress and tell the beam search which tokens to generate next. Although we have provided the keyword argument force_words_ids for model.generate(), the following is what actually happens in the back-end:
from transformers import AutoTokenizer, AutoModelForSeq2SeqLM, PhrasalConstraint
tokenizer = AutoTokenizer.from_pretrained("t5-base")
model = AutoModelForSeq2SeqLM.from_pretrained("t5-base")
encoder_input_str = "translate English to German: How old are you?"
constraints = [
PhrasalConstraint(
tokenizer("Sie", add_special_tokens=False).input_ids
)
]
input_ids = tokenizer(encoder_input_str, return_tensors="pt").input_ids
outputs = model.generate(
input_ids,
constraints=constraints,
num_beams=10,
num_return_sequences=1,
no_repeat_ngram_size=1,
remove_invalid_values=True,
)
print("Output:\n" + 100 * '-')
print(tokenizer.decode(outputs[0], skip_special_tokens=True))Output:
----------------------------------------------------------------------------------------------------
Wie alt sind Sie?
You can define one yourself and input it into the constraints keyword argument to design your unique constraints. You just have to create a sub-class of the Constraint abstract interface class and follow its requirements. You can find more information in the definition of Constraint found here.
Some unique ideas (not yet implemented; maybe you can give it a try!) include constraints like OrderedConstraints, TemplateConstraints that may be added further down the line. Currently, the generation is fulfilled by including the sequences, wherever in the output. For example, a previous example had one sequence with scared -> screaming and the other with screamed -> scared. OrderedConstraints could allow the user to specify the order in which these constraints are fulfilled.
TemplateConstraints could allow for a more niche use of the feature, where the objective can be something like:
starting_text = "The woman"
template = ["the", "", "School of", "", "in"]
possible_outputs == [
"The woman attended the Ross School of Business in Michigan.",
"The woman was the administrator for the Harvard School of Business in MA."
]or:
starting_text = "The woman"
template = ["the", "", "", "University", "", "in"]
possible_outputs == [
"The woman attended the Carnegie Mellon University in Pittsburgh.",
]
impossible_outputs == [
"The woman attended the Harvard University in MA."
]or if the user does not care about the number of tokens that can go in between two words, then one can just use OrderedConstraint.
Constrained beam search gives us a flexible means to inject external knowledge and requirements into text generation. Previously, there was no easy way to tell the model to 1. include a list of sequences where 2. some of which are optional and some are not, such that 3. they're generated somewhere in the sequence at respective reasonable positions. Now, we can have full control over our generation with a mix of different subclasses of Constraint objects!
This new feature is based mainly on the following papers:
- Guided Open Vocabulary Image Captioning with Constrained Beam Search
- Fast Lexically Constrained Decoding with Dynamic Beam Allocation for Neural Machine Translation
- Improved Lexically Constrained Decoding for Translation and Monolingual Rewriting
- Guided Generation of Cause and Effect
Like the ones above, many new research papers are exploring ways of using external knowledge (e.g., KGs, KBs) to guide the outputs of large deep learning models. Hopefully, this constrained beam search feature becomes another effective way to achieve this purpose.
Thanks to everybody that gave guidance for this feature contribution: Patrick von Platen for being involved from the initial issue to the final PR, and Narsil Patry, for providing detailed feedback on the code.
Thumbnail of this post uses an icon with the attribution: Shorthand icons created by Freepik - Flaticon