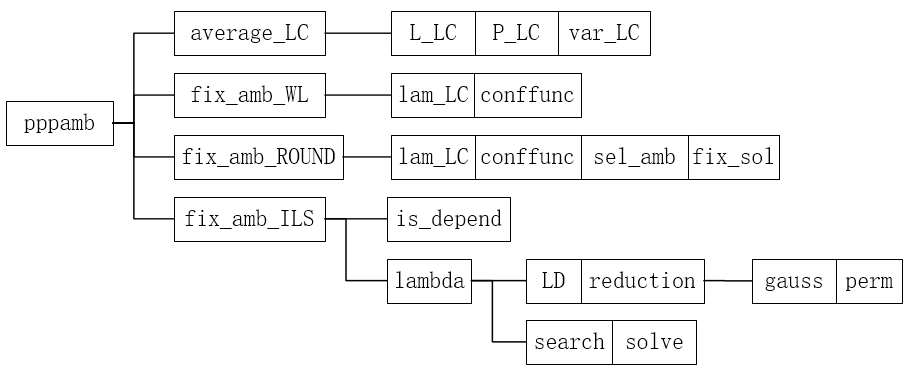
[TOC]

一、pppos()：精密单点定位主入口函数

1、函数调用流程图

2、传入参数

rtk_t    *rtk      IO  rtk控制结构体
obsd_t   *obs      I   OBS观测数据
int      n         I   OBS观测数据的数量
nav_t    *nav      I   导航数据

3、执行流程

遍历所有卫星、所有频率，结果rtk->ssat[i].fix[j]赋值0
时间更新：调用udstate_ppp()，更新状态值rtk->x及其误差协方差rtk->P
调用satposs()，计算卫星位置rs、卫星钟差dts
调用testeclipse()，排除需要排除的卫星
调用tidedisp()，计算海洋潮汐以及极潮对接收机位置产生的影响
滤波迭代、默认次数(8次)
- 调用matcpy()，复制 rtk->x到xp，rtk->P到Pp
- 调用ppp_res()，计算残差V，设计矩阵H
- 调用filter()，kalman滤波量测更新解算出xp、Pp
- 解算后，进行后验残差估计，符合限制则输出为精密单点定位状态，将解算结果xp、Pp赋值到rtk->x、rtk->P，break迭代
如果迭代次数超过设置次数，输出“迭代溢出”
如果解的状态是SOLQ_PPP
- 调用ppp_ar()进行模糊度固定，ppp_res()进行后验残差估计
- 检验通过，将解算结果xp、Pp赋值到rtk->xa、rtk->Pa，计算三个未知参数的方差，方差向量的模如果<MAX_STD_FIX，解的状态设为固定解SOLQ_FIX
- 检验不通过，rtk->nfix值设置为0
- 调用update_stat()，更新solution状态

extern void pppos(rtk_t *rtk, const obsd_t *obs, int n, const nav_t *nav)
{
    const prcopt_t *opt=&rtk->opt;
    double *rs,*dts,*var,*v,*H,*R,*azel,*xp,*Pp,dr[3]={0},std[3];
    char str[32];
    int i,j,nv,info,svh[MAXOBS],exc[MAXOBS]={0},stat=SOLQ_SINGLE;
    
    time2str(obs[0].time,str,2);
    trace(3,"pppos   : time=%s nx=%d n=%d\n",str,rtk->nx,n);
    
    rs=mat(6,n); dts=mat(2,n); var=mat(1,n); azel=zeros(2,n);
    
    //遍历所有卫星、所有频率，rtk->ssat[i].fix[j]赋值0
    for (i=0;i<MAXSAT;i++) for (j=0;j<opt->nf;j++) rtk->ssat[i].fix[j]=0;
    //卡尔曼滤波的时间更新，分为位置参数更新，钟差参数更新，对流层、电离层。相位偏差的时间参数更新
    //更新状态值 rtk->x 及其误差协方差 rtk->P
    /* temporal update of ekf states */
    udstate_ppp(rtk,obs,n,nav);     
    
    /* satellite positions and clocks */    //计算卫星位置rs、卫星钟差dts
    satposs(obs[0].time,obs,n,nav,rtk->opt.sateph,rs,dts,var,svh);
    
    /* exclude measurements of eclipsing satellite (block IIA) */
    if (rtk->opt.posopt[3]) {   //调用 testeclipse 进行排除需要排除的卫星
        testeclipse(obs,n,nav,rs);
    }
    /* earth tides correction */    //计算海洋潮汐以及极潮对接收机位置产生的影响
    if (opt->tidecorr) {
        tidedisp(gpst2utc(obs[0].time),rtk->x,opt->tidecorr==1?1:7,&nav->erp,
                 opt->odisp[0],dr);
    }
    nv=n*rtk->opt.nf*2+MAXSAT+3;    
    xp=mat(rtk->nx,1); 
    Pp=zeros(rtk->nx,rtk->nx);
    v=mat(nv,1);        //残差 v 
    H=mat(rtk->nx,nv);  //设计矩阵 H
    R=mat(nv,nv);       //测量误差的协方差 R
    
    //滤波迭代、默认次数(8次) 
    for (i=0;i<MAX_ITER;i++) {  
        
        matcpy(xp,rtk->x,rtk->nx,1);
        matcpy(Pp,rtk->P,rtk->nx,rtk->nx);  
        
        /* prefit residuals */  
        if (!(nv=ppp_res(0,obs,n,rs,dts,var,svh,dr,exc,nav,xp,rtk,v,H,R,azel))) {
            trace(2,"%s ppp (%d) no valid obs data\n",str,i+1);
            break;
        }   

        /* measurement update of ekf states */
        if ((info=filter(xp,Pp,H,v,R,rtk->nx,nv))) {    //扩展卡尔曼滤波量测更新，
                // filter用于EKF状态的量测更新，先验状态和后验状态信息的更新
                // filter_进行EKF，量测更新部分的解算                                                            
            trace(2,"%s ppp (%d) filter error info=%d\n",str,i+1,info);
            break;
        }
        /* postfit residuals */ //解算后，进行后验残差估计，符合限制则输出为精密单点定位状态
        if (ppp_res(i+1,obs,n,rs,dts,var,svh,dr,exc,nav,xp,rtk,v,H,R,azel)) {
            matcpy(rtk->x,xp,rtk->nx,1);
            matcpy(rtk->P,Pp,rtk->nx,rtk->nx);
            stat=SOLQ_PPP;
            break;      //结束迭代
        }
    }
    if (i>=MAX_ITER) {
        trace(2,"%s ppp (%d) iteration overflows\n",str,i);
    }
    if (stat==SOLQ_PPP) {
        
        /* ambiguity resolution in ppp */   //模糊度固定，RTKLIB中的ppp_ar没实现直接return 0
        if (ppp_ar(rtk,obs,n,exc,nav,azel,xp,Pp)&&
            ppp_res(9,obs,n,rs,dts,var,svh,dr,exc,nav,xp,rtk,v,H,R,azel)) {     //ppp_res计算残差
            
            matcpy(rtk->xa,xp,rtk->nx,1);
            matcpy(rtk->Pa,Pp,rtk->nx,rtk->nx);
            
            for (i=0;i<3;i++) std[i]=sqrt(Pp[i+i*rtk->nx]);
            if (norm(std,3)<MAX_STD_FIX) stat=SOLQ_FIX;
        }
        else {
            rtk->nfix=0;
        }
        /* update solution status */
        update_stat(rtk,obs,n,stat);    //更新solution状态
        
        /* hold fixed ambiguities */
        if (stat==SOLQ_FIX&&test_hold_amb(rtk)) {
            matcpy(rtk->x,xp,rtk->nx,1);
            matcpy(rtk->P,Pp,rtk->nx,rtk->nx);
            trace(2,"%s hold ambiguity\n",str);
            rtk->nfix=0;
        }
    }
    free(rs); free(dts); free(var); free(azel);
    free(xp); free(Pp); free(v); free(H); free(R);
}

二、udstate_ppp()：Kalman滤波时间更新

1、传入参数

rtk_t    *rtk      IO  rtk控制结构体
obsd_t   *obs      I   OBS观测数据
int      n         I   OBS观测数据的数量
nav_t    *nav      I   导航数据

2、执行流程

调用udpos_ppp()，位置参数更新
调用udclk_ppp()，钟差参数更新
如果在配置中选择的对流层模型为ZTD estimation或者ZTD+grad estimation，调用udtrop_ppp()，对流层参数更新
如果在配置中选择电离层模型为estimation，调用udiono_ppp()，电离层参数更新
如果选择的频率数>=3，调用uddcb_ppp()，L5接收机硬件延迟参数更新
调用udbias_ppp()，整周模糊度参数更新

static void udstate_ppp(rtk_t *rtk, const obsd_t *obs, int n, const nav_t *nav)
{
    trace(3,"udstate_ppp: n=%d\n",n);
    
    /* temporal update of position */   //调用 udpos_ppp 根据不同模式初始化状态 rtk->x 中的位置值
    udpos_ppp(rtk);     //位置参数更新
    
    /* temporal update of clock */  //调用 udclk_ppp 初始化状态 rtk->x 中的钟差值（6个，因有6个系统）
    udclk_ppp(rtk);     //钟差参数更新
    
    /* temporal update of tropospheric parameters */
    if (rtk->opt.tropopt==TROPOPT_EST||rtk->opt.tropopt==TROPOPT_ESTG) {
        udtrop_ppp(rtk);    //对流层参数更新
    }
    /* temporal update of ionospheric parameters */
    if (rtk->opt.ionoopt==IONOOPT_EST) {
        udiono_ppp(rtk,obs,n,nav);  //电离层参数更新
    }
    /* temporal update of L5-receiver-dcb parameters */
    if (rtk->opt.nf>=3) {
        uddcb_ppp(rtk);     //更新L5接收机硬件延迟参数
    }
    /* temporal update of phase-bias */ //调用 udbias_ppp 更新载波相位偏移状态值以及其误差协方差。
    udbias_ppp(rtk,obs,n,nav);      //整周模糊度更新
}

3、udpos_ppp()：位置参数更新

执行流程：

如果是PPP固定解模式PMODE_PPP_FIXED，直接用已知点的固定坐标初始化
如果是首历元，赋值单点定位的解rtk->sol.rr、VAR_POS，动力学模式，还要赋值速度、加速度
如果是PPP静态PMODE_PPP_STATIC模式，状态量不变，只给P矩阵加过程噪声
如果PMODE_PPP_KINEMA但非dynamics模式，用单点定位解rtk->sol.rr[i]和VAR_POS赋值
动力学模式动态PPP，构建状态转移矩阵F，进行状态转移
为Q矩阵加速度部分加过程噪声

static void udpos_ppp(rtk_t *rtk)
{
    double *F,*P,*FP,*x,*xp,pos[3],Q[9]={0},Qv[9];
    int i,j,*ix,nx;
    
    trace(3,"udpos_ppp:\n");
    
    //如果是PPP固定解模式，直接用已知点的固定坐标初始化
    /* fixed mode */
    if (rtk->opt.mode==PMODE_PPP_FIXED) {       
        for (i=0;i<3;i++) initx(rtk,rtk->opt.ru[i],1E-8,i);
        return;
    }
    //如果是首历元，赋值单点定位的解
    /* initialize position for first epoch */
    if (norm(rtk->x,3)<=0.0) {
        for (i=0;i<3;i++) initx(rtk,rtk->sol.rr[i],VAR_POS,i);
        if (rtk->opt.dynamics) {    //动力学模式，赋值速度、加速度
            for (i=3;i<6;i++) initx(rtk,rtk->sol.rr[i],VAR_VEL,i);
            for (i=6;i<9;i++) initx(rtk,1E-6,VAR_ACC,i);
        }
    }
    //如果是PMODE_PPP_STATIC 模式，状态量不变，只给P矩阵加过程噪声
    /* static ppp mode */
    if (rtk->opt.mode==PMODE_PPP_STATIC) {      
        for (i=0;i<3;i++) {
            rtk->P[i*(1+rtk->nx)]+=SQR(rtk->opt.prn[5])*fabs(rtk->tt);
        }
        return;
    }

    //如果PMODE_PPP_KINEMA但非dynamics模式，用单点定位解rtk->sol.rr[i]和VAR_POS赋值
    /* kinmatic mode without dynamics */    
    if (!rtk->opt.dynamics) {
        for (i=0;i<3;i++) {
            initx(rtk,rtk->sol.rr[i],VAR_POS,i);
        }
        return;
    }
    //动力学模式动态 PPP，构建状态转移矩阵 F
    /* generate valid state index */        
    ix=imat(rtk->nx,1);
    for (i=nx=0;i<rtk->nx;i++) {
        if (rtk->x[i]!=0.0&&rtk->P[i+i*rtk->nx]>0.0) ix[nx++]=i;
    }
    if (nx<9) {     //参数需要大于 9 个
        free(ix);
        return;
    }
    
    //状态转移矩阵构建
    /* state transition of position/velocity/acceleration */    
    F=eye(nx); P=mat(nx,nx); FP=mat(nx,nx); x=mat(nx,1); xp=mat(nx,1);   
    for (i=0;i<6;i++) {
        F[i+(i+3)*nx]=rtk->tt;
    }
    for (i=0;i<3;i++) {
        F[i+(i+6)*nx]=SQR(rtk->tt)/2.0;
    }
    for (i=0;i<nx;i++) {
        x[i]=rtk->x[ix[i]];
        for (j=0;j<nx;j++) {
            P[i+j*nx]=rtk->P[ix[i]+ix[j]*rtk->nx];
        }
    }
    // 状态转移
    /* x=F*x, P=F*P*F+Q */
    matmul("NN",nx,1,nx,1.0,F,x,0.0,xp);
    matmul("NN",nx,nx,nx,1.0,F,P,0.0,FP);
    matmul("NT",nx,nx,nx,1.0,FP,F,0.0,P);
    
    for (i=0;i<nx;i++) {
        rtk->x[ix[i]]=xp[i];
        for (j=0;j<nx;j++) {
            rtk->P[ix[i]+ix[j]*rtk->nx]=P[i+j*nx];
        }
    }

    //为 Q 矩阵加速度部分加过程噪声
    /* process noise added to only acceleration */  
    Q[0]=Q[4]=SQR(rtk->opt.prn[3])*fabs(rtk->tt);
    Q[8]=SQR(rtk->opt.prn[4])*fabs(rtk->tt);
    ecef2pos(rtk->x,pos);   //XYZ->BLH
    covecef(pos,Q,Qv);
    for (i=0;i<3;i++) for (j=0;j<3;j++) {
        rtk->P[i+6+(j+6)*rtk->nx]+=Qv[i+j*3];
    }
    free(ix); free(F); free(P); free(FP); free(x); free(xp);
}

4、udclk_ppp()：钟差参数更新

执行流程：

检测是否为精密星历EPHOPT_PREC，认为精密钟差是白噪声，每个历元初始化，精密星历的时间是基于 GPS 时间，忽略系统间的偏差
不是精密星历则利用前一秒的结果，并考虑系统间时差信息

static void udclk_ppp(rtk_t *rtk)
{
    double dtr;
    int i;
    
    trace(3,"udclk_ppp:\n");

    //认为钟差是白噪声,每个历元初始化
    /* initialize every epoch for clock (white noise) */    
    for (i=0;i<NSYS;i++) {
        //检测是否为精密星历EPHOPT_PREC，精密星历的时间是基于gps时间，忽略系统间的偏差
        if (rtk->opt.sateph==EPHOPT_PREC) {     //精密星历
            /* time of prec ephemeris is based gpst */
            /* negelect receiver inter-system bias  */
            dtr=rtk->sol.dtr[0];
        }
        //不是精密星历则利用前一秒的结果，并考虑系统间时差信息
        else {
            dtr=i==0?rtk->sol.dtr[0]:rtk->sol.dtr[0]+rtk->sol.dtr[i];
        }
        initx(rtk,CLIGHT*dtr,VAR_CLK,IC(i,&rtk->opt));
    }
}

5、udtrop_ppp()：对流层参数更新

6、udiono_ppp()：电离层参数更新

7、uddcb_ppp()：L5接收机硬件延迟参数更新

8、udbias_ppp()：整周模糊度参数更新

1.传入参数

IO    rtk_t *rtk			rtk solution structure
I     const obsd_t *obs	当前历元观测值
I     int n 				当前移动站观测值数目
I     const nav_t *nav     星历

2.执行流程

日界线检测
周跳检测：清除卫星周跳标志位rtk->ssat[i].slip，调用detslp_ll()，通过LLI检测周跳，调用detslp_gf()，通过几何无关组合检测周跳，调用detslp_mw()，MW组合检测周跳
遍历各个频点：
遍历各个卫星，判断是否需要重置单差相位偏移状态量，如果检测到相位中断大于门限，或ARMODE_INST单历元模糊度固定模式，或检测到时钟跳变，则重新赋值模糊度参数。
遍历各个卫星，对每一组观测数据，调用corrmeas()，进行天线相位中心修正，相位缠绕修正，卫星硬件延迟修正
bias赋赋值0；消电离层模式，不用再考虑电离层延迟，直接计算bias[i]=Lc-Pc，否则先通过双频伪距计算电离层延迟ion=(obs[i].P[0]-obs[i].P[f])/(1.0-SQR(freq1/freq2));，利用修正后的电离层延迟计算bias[i]=L[f]-P[f]+2.0*ion*SQR(freq1/freq2);
检测值是否有效，是否周跳，如果正常，统计初始模糊度和状态量之间的整体偏差offset
判断如果满足补偿门限，若载波和伪距跳变太大，为了保持一致性，需要进行校正，在原有的载波相位偏差状态量上加上offset的平均值，以此来作为载波相位偏差的时间更新
遍历各个卫星，给P矩阵加过程噪声
如果状态量无效，或有周跳发生，则用偏移值bias重置rtk->x，重置模糊度固定标志位rtk->ambc[sat-1].flags[k]=0

八、PPP-AR

ppp_ar.c 的内容在最新版的 RTKLIB 被删除了，这里介绍的是之前 2.4.2 版本的。

1、pppamb()：PPP 模糊度固定入口函数

双频的宽巷就是两频率求和，窄巷就是两频率做差。宽巷组合具有较长的波长和非常小的载波方差，有利于模糊度的求解，但是放大了测量噪声；窄巷组合具有较小的距离方差，有利于基线矢量的精度，但是波长短，载波方差较大，不利于模糊度的求解。所以先固定较容易的宽巷模糊度，再固定窄向模糊度以获得更高的精度。

2、average_LC()：计算平均线性组合

L_LC()、P_LC()、var_LC()、Lam_LC() 是进行线性组合的基本函数，分别用于计算组合（三频或双频）后的载波、伪距、方差、波长。

3、fix_amb_WL()：均值取整法固定宽巷模糊度

4、fix_amb_ROUND()：取整法固定窄巷模糊度

直接取整法不是很靠谱，容易导致模糊度固定错误，固定解可能还没有浮点解精度高。

5、fix_amb_ILS()：整数最小二乘法固定窄向模糊度

6、lambda()：最小二乘模糊度去相关法

传入参数：

int    n      I  number of float parameters      //浮点解数量
int    m      I  number of fixed solutions       //固定解数量
double *a     I  float parameters (n x 1)        //浮点参数向量
double *Q     I  covariance matrix of float parameters (n x n)   //浮点参数协方差阵
double *F     O  fixed solutions (n x m)     	//固定解
double *s     O  sum of squared residulas of fixed solutions (1 x m) //总固定残差向量

执行流程：

调用LD()，首先对浮点协方差阵进行LD分解
调用reduction()，lambda降相关性
z变换，将双差模糊度进行变换
调用search(),mlambda search，结果存储在E和s中（整数解）
调用solve()，逆Z变换，将在新空间中固定的模糊度逆变换回双差模糊度空间中，存储在F中

extern int lambda(int n, int m, const double *a, const double *Q, double *F,
                  double *s)
{
    int info;
    double *L,*D,*Z,*z,*E;
    
    if (n<=0||m<=0) return -1;
    L=zeros(n,n); D=mat(n,1); Z=eye(n); z=mat(n,1); E=mat(n,m);
    
    //调用LD()，首先对浮点协方差阵进行LD分解
    /* LD factorization */
    if (!(info=LD(n,Q,L,D))) {

        //调用reduction()，lambda降相关性
        /* lambda reduction */
        reduction(n,L,D,Z);

        // z变换，将双差模糊度进行变换
        matmul("TN",n,1,n,1.0,Z,a,0.0,z); /* z=Z'*a */
        
        //调用search(),mlambda search，结果存储在E和s中（整数解）
        /* mlambda search */
        if (!(info=search(n,m,L,D,z,E,s))) {
            //逆Z变换，将在新空间中固定的模糊度逆变换回双差模糊度空间中，存储在F中
            info=solve("T",Z,E,n,m,F); /* F=Z'\E */
        }
    }
    free(L); free(D); free(Z); free(z); free(E);
    return info;
}

1. reduction()：LAMBDA降相关

static void reduction(int n, double *L, double *D, double *Z)
{
    int i,j,k;
    double del;
    
    j=n-2; k=n-2;   //调序变换
    
    //对第0,1，...，k-1，k列进行降相关
    while (j>=0) {
        if (j<=k) for (i=j+1;i<n;i++) gauss(n,L,Z,i,j); //从最后一列开始，各列非对角线元素从上往下依次降相关
        del=D[j]+L[j+1+j*n]*L[j+1+j*n]*D[j+1];
        //检验条件，若不满足检验条件则开始进行调序变换
        if (del+1E-6<D[j+1]) { /* compared considering numerical error */
            perm(n,L,D,j,del,Z);
            k=j; j=n-2; //完成调序变换后重新从最后一列开始进行降相关及排序，k记录最后一次进行过调序变换的列序号
        }
        else j--;
    }
}

2. gauss()：整数高斯变换

static void gauss(int n, double *L, double *Z, int i, int j)
{
    int k,mu;
    
    if ((mu=(int)ROUND(L[i+j*n]))!=0) {
        for (k=i;k<n;k++) L[k+n*j]-=(double)mu*L[k+i*n];
        for (k=0;k<n;k++) Z[k+n*j]-=(double)mu*Z[k+i*n];
    }
}

3. perm()：条件方差重新排列

static void perm(int n, double *L, double *D, int j, double del, double *Z)
{
    int k;
    double eta,lam,a0,a1;
    
    eta=D[j]/del;
    lam=D[j+1]*L[j+1+j*n]/del;
    D[j]=eta*D[j+1]; D[j+1]=del;
    for (k=0;k<=j-1;k++) {
        a0=L[j+k*n]; a1=L[j+1+k*n];
        L[j+k*n]=-L[j+1+j*n]*a0+a1;
        L[j+1+k*n]=eta*a0+lam*a1;
    }
    L[j+1+j*n]=lam;
    for (k=j+2;k<n;k++) SWAP(L[k+j*n],L[k+(j+1)*n]);
    for (k=0;k<n;k++) SWAP(Z[k+j*n],Z[k+(j+1)*n]);
}

4. search()：mlambda搜索

static int search(int n, int m, const double *L, const double *D,
                  const double *zs, double *zn, double *s)
{
    int i,j,k,c,nn=0,imax=0;
    double newdist,maxdist=1E99,y;
    double *S=zeros(n,n),*dist=mat(n,1),*zb=mat(n,1),*z=mat(n,1),*step=mat(n,1);
    
    k=n-1; dist[k]=0.0; //k表示当前层，从最后一层（n-1）开始计算
    zb[k]=zs[k];//即zn
    z[k]=ROUND(zb[k]); y=zb[k]-z[k]; step[k]=SGN(y);    //四舍五入取整；取整后的数与未取整的数作差；step记录z[k]是四舍还是五入
    for (c=0;c<LOOPMAX;c++) {
        newdist=dist[k]+y*y/D[k];
        if (newdist<maxdist) {      //如果当前累积目标函数计算值小于当前超椭圆半径
            //情况1：若还未计算至第一层，继续计算累积目标函数值
            if (k!=0) { 
                dist[--k]=newdist;  //记录下当前层的累积目标函数值，dist[k]表示了第k,k+1,...,n-1层的目标函数计算和
                for (i=0;i<=k;i++)
                    S[k+i*n]=S[k+1+i*n]+(z[k+1]-zb[k+1])*L[k+1+i*n];
                zb[k]=zs[k]+S[k+k*n];   //计算Zk，即第k个整数模糊度参数的备选组的中心
                z[k]=ROUND(zb[k]); y=zb[k]-z[k]; step[k]=SGN(y);    //四舍五入取整；取整后的数与未取整的数作差；记录是四舍还是五入
            }
            //情况2：若已经计算至第一层，意味着所有层的累积目标函数值计算完毕
            else {
                //nn为当前候选解数，m为我们需要的固定解数，这里为2，表示需要一个最优解及一个次优解
                //s记录候选解的目标函数值，imax记录之前候选解中的最大目标函数值的坐标
                if (nn<m) { //若候选解数还没满
                    if (nn==0||newdist>s[imax]) imax=nn;    //若当前解的目标函数值比之前最大的目标函数值都大，那么更新imax使s[imax]指向当前解中具有的最大目标函数值
                    for (i=0;i<n;i++) zn[i+nn*n]=z[i];  //zn存放所有候选解
                    s[nn++]=newdist;    //s记录当前目标函数值newdist，并加加当前候选解数nn
                }
                else {  //若候选解数已满（即当前zn中已经存了2个候选解）
                    if (newdist<s[imax]) {  //若当前解的目标函数值比s中的最大目标函数值 
                        for (i=0;i<n;i++) zn[i+imax*n]=z[i];    //用当前解替换zn中具有较大目标函数值的解
                        s[imax]=newdist;    //用当前解的目标函数值替换s中的最大目标函数值
                        for (i=imax=0;i<m;i++) if (s[imax]<s[i]) imax=i;    //更新imax保证imax始终指向s中的最大目标函数值
                    }
                    maxdist=s[imax];    //用当前最大的目标函数值更新超椭圆半径
                }
                //在第一层，取下一个有效的整数模糊度参数进行计算（若zb为5.3，则z取值顺序为5,6,4,7，...）
                z[0]+=step[0]; y=zb[0]-z[0]; step[0]=-step[0]-SGN(step[0]);
            }
        }
        //情况3：如果当前累积目标函数计算值大于当前超椭圆半径
        else {
            if (k==n-1) break;  //如果当前层为第n-1层，意味着后续目标函数各项的计算都会超出超椭圆半径，因此终止搜索
            else {  //若当前层不是第n-1层
                k++;    //退后一层，即从第k层退到第k+1层
                z[k]+=step[k]; y=zb[k]-z[k]; step[k]=-step[k]-SGN(step[k]); //计算退后一层后，当前层的下一个有效备选解
            }
        }
    }
    // 对s中的目标函数值及zn中的候选解进行排序（以s中目标函数值为排序标准，进行升序排序）
    // RTKLIB中最终可以得到一个最优解一个次优解，存在zn中，两解对应的目标函数值，存在s中
    for (i=0;i<m-1;i++) { /* sort by s */
        for (j=i+1;j<m;j++) {
            if (s[i]<s[j]) continue;
            SWAP(s[i],s[j]);
            for (k=0;k<n;k++) SWAP(zn[k+i*n],zn[k+j*n]);
        }
    }
    free(S); free(dist); free(zb); free(z); free(step);
    
    if (c>=LOOPMAX) {
        fprintf(stderr,"%s : search loop count overflow\n",__FILE__);
        return -1;
    }
    return 0;
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

12-RTKLIB源码阅读（十二）精密单点定位 PPP.md

12-RTKLIB源码阅读（十二）精密单点定位 PPP.md

一、pppos()：精密单点定位主入口函数

1、函数调用流程图

2、传入参数

3、执行流程

二、udstate_ppp()：Kalman滤波时间更新

1、传入参数

2、执行流程

3、udpos_ppp()：位置参数更新

4、udclk_ppp()：钟差参数更新

5、udtrop_ppp()：对流层参数更新

6、udiono_ppp()：电离层参数更新

7、uddcb_ppp()：L5接收机硬件延迟参数更新

8、udbias_ppp()：整周模糊度参数更新

1.传入参数

2.执行流程

八、PPP-AR

1、pppamb()：PPP 模糊度固定入口函数

2、average_LC()：计算平均线性组合

3、fix_amb_WL()：均值取整法固定宽巷模糊度

4、fix_amb_ROUND()：取整法固定窄巷模糊度

5、fix_amb_ILS()：整数最小二乘法固定窄向模糊度

6、lambda()：最小二乘模糊度去相关法

1. reduction()：LAMBDA降相关

2. gauss()：整数高斯变换

3. perm()：条件方差重新排列

4. search()：mlambda搜索

Files

12-RTKLIB源码阅读（十二）精密单点定位 PPP.md

Latest commit

History

12-RTKLIB源码阅读（十二）精密单点定位 PPP.md

File metadata and controls

一、pppos()：精密单点定位主入口函数

1、函数调用流程图

2、传入参数

3、执行流程

二、udstate_ppp()：Kalman滤波时间更新

1、传入参数

2、执行流程

3、udpos_ppp()：位置参数更新

4、udclk_ppp()：钟差参数更新

5、udtrop_ppp()：对流层参数更新

6、udiono_ppp()：电离层参数更新

7、uddcb_ppp()：L5接收机硬件延迟参数更新

8、udbias_ppp()：整周模糊度参数更新

1.传入参数

2.执行流程

八、PPP-AR

1、pppamb()：PPP 模糊度固定入口函数

2、average_LC()：计算平均线性组合

3、fix_amb_WL()：均值取整法固定宽巷模糊度

4、fix_amb_ROUND()：取整法固定窄巷模糊度

5、fix_amb_ILS()：整数最小二乘法固定窄向模糊度

6、lambda()：最小二乘模糊度去相关法

1. reduction()：LAMBDA降相关

2. gauss()：整数高斯变换

3. perm()：条件方差重新排列

4. search()：mlambda搜索