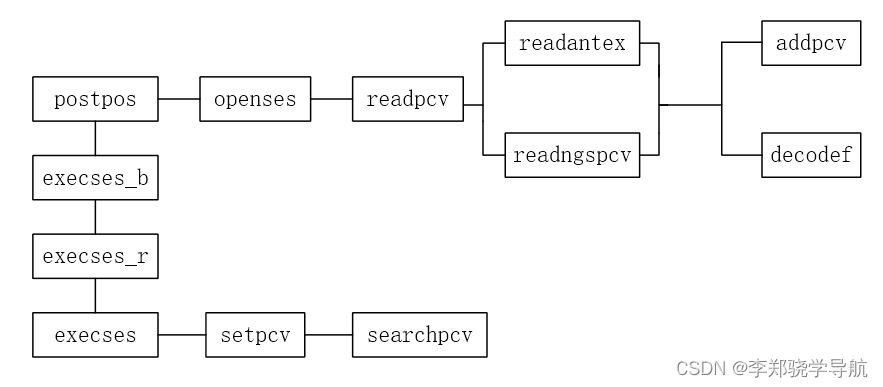
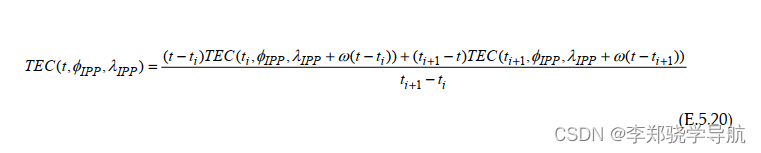原始 Markdown文档、Visio流程图、XMind思维导图见:https://github.com/LiZhengXiao99/Navigation-Learning
[TOC]
模型公式见 manual p151,我在代码的注释里标注了公式号
-
卫星 GNSS 电磁波信号在传播过程中需要穿过地球大气层,会产生一些大气延迟误差, 包括电离层延迟误差和对流层延迟误差。
-
电离层的范围从离地面约 50 公里开始一直伸展到约 1000 公里高度的地球高层大气空域。电离层的主要特性由电子密度、电子温度、碰撞频率、离子密度、离子温度和离子成分等空间分布的基本参数来表示。电离层的研究对象主要是电子密度随高度的分布。电子密度(或称电子浓度)是指单位体积的自由电子数,随高度的变化与各高度上大气成分、大气密度以及太阳辐射通量等因素有关。电离层内任一点上的电子密度,决定于上述自由电子的产生、消失和迁移三种效应。在不同区域,三者的相对作用和各自的具体作用方式也大有差异。电离层中存在相当多的自由电子和离子,能使无线电波改变传播速度,发生折射、反射和散射,产生极化面的旋转并受到不同程度的吸收。
-
电离层延迟与单位面积的横截面在信号传播路径上拦截的电子总量
$N_e$ 成正比,且与载波频率$f$ 的平方成反比,弥散性的电离层降低了测距码的传播速度,而加快了载波相位的传播速度,如下所示。 $$ I=I_ \rho=-I_\phi=40.28\frac{N_e}{f^2} $$ -
由于电离层的三维结构,其电子密度在水平和垂直方向上分布都不均匀,对于 GNSS 信号,其电离层延迟是整个传播路径上电子密度的积分,因此延迟量与信号的高度角、方位角相关。然而电子密度的具体分布对实际 GNSS 数据处理影响不大,GNSS 用户更关心信号传播路径上的总电子含量,为了简化计算,在 GNSS 数据处理中引入了单层假设的概念,即将整个电离层压缩为一个高度为 H 的无限薄层,并假定电离层中所有的自由电子都集中分布在这个薄层上,在该薄层上,对VTEC进行计算和处理,示意图如下:
-
传统的双频测地型接收机通常使用双频观测值无电离层组合的方式消除一阶电离层延迟 误差,而对于单频数据,则通常采用电离层模型改正的方式来削弱电离层误差影响。常用的 电离层延迟改正模型包括克罗布歇(Klobuchar)模型、格网(Global Ionosphere Maps,GIM)、模型和国际参考电离层(International Reference Ionosphere,IRI)模型等。
在 rescode() 中被调用,根据选项,调用 ionmodel()、sbsioncorr()、iontec()、ionmodel() 计算 L1 载波电离层延迟 I
计算的是 L1 信号的电离层延时 I,当使用其它频率信号时,依据所用信号频组中第一个频率的波长与 L1 波长的比例关系,对上一步得到的电离层延时进行修正。
rescode() 函数中的使用:
if (!ionocorr(time,nav,sat,pos,azel+i*2,opt->ionoopt,&dion,&vion)) continue; if ((freq=sat2freq(sat,obs[i].code[0],nav))==0.0) continue; dion*=SQR(FREQ1/freq); //电离层改正量 vion*=SQR(FREQ1/freq); //电离层改正误差
extern int ionocorr(gtime_t time, const nav_t *nav, int sat, const double *pos,
const double *azel, int ionoopt, double *ion, double *var)
{
trace(4,"ionocorr: time=%s opt=%d sat=%2d pos=%.3f %.3f azel=%.3f %.3f\n",
time_str(time,3),ionoopt,sat,pos[0]*R2D,pos[1]*R2D,azel[0]*R2D,
azel[1]*R2D);
/* GPS broadcast ionosphere model */
if (ionoopt==IONOOPT_BRDC) { //广播星历模型
*ion=ionmodel(time,nav->ion_gps,pos,azel);
*var=SQR(*ion*ERR_BRDCI);
return 1;
}
/* SBAS ionosphere model */
if (ionoopt==IONOOPT_SBAS) { //SBAS校正
return sbsioncorr(time,nav,pos,azel,ion,var);
}
/* IONEX TEC model */
if (ionoopt==IONOOPT_TEC) { //电子总量格网模型
return iontec(time,nav,pos,azel,1,ion,var);
}
/* QZSS broadcast ionosphere model */ //QZSS广播星历模型
if (ionoopt==IONOOPT_QZS&&norm(nav->ion_qzs,8)>0.0) {
*ion=ionmodel(time,nav->ion_qzs,pos,azel);
*var=SQR(*ion*ERR_BRDCI);
return 1;
}
*ion=0.0;
*var=ionoopt==IONOOPT_OFF?SQR(ERR_ION):0.0; //有电离层改正,方差为0,无电离层改正,方差5*5
return 1;
}即(klobuchar model)克罗布歇模型,用 8 个电离层参数模型校正
卫星在其播发的导航电文中提供电离层延迟参数,接收机根据参数$\alpha_0,\alpha_1,\alpha_2,\alpha_3$确定振幅$A$,根据参数
$\beta_0,\beta_1,\beta_2,\beta_3$ 确定周期$T$,再给定一个以秒为单位的当地时间$T$ ,就能算出天顶电离层延迟。再由天顶对流层延迟根据倾斜率转为卫星方向对流层延迟。
extern double ionmodel(gtime_t t, const double *ion, const double *pos,
const double *azel)
{
const double ion_default[]={ /* 2004/1/1 */
0.1118E-07,-0.7451E-08,-0.5961E-07, 0.1192E-06,
0.1167E+06,-0.2294E+06,-0.1311E+06, 0.1049E+07
};
double tt,f,psi,phi,lam,amp,per,x;
int week;
if (pos[2]<-1E3||azel[1]<=0) return 0.0;
if (norm(ion,8)<=0.0) ion=ion_default; //若没有电离层参数,用默认参数
/* earth centered angle (semi-circle) */ //地球中心角
psi=0.0137/(azel[1]/PI+0.11)-0.022; //计算地心角(E.5.6)
/* subionospheric latitude/longitude (semi-circle) */
phi=pos[0]/PI+psi*cos(azel[0]); //计算穿刺点地理纬度(E.5.7)
if (phi> 0.416) phi= 0.416; //phi不超出(-0.416,0.416)范围
else if (phi<-0.416) phi=-0.416;
lam=pos[1]/PI+psi*sin(azel[0])/cos(phi*PI); //计算穿刺点地理经度(E.5.8)
/* geomagnetic latitude (semi-circle) */
phi+=0.064*cos((lam-1.617)*PI); //计算穿刺点地磁纬度(E.5.9)
/* local time (s) */
tt=43200.0*lam+time2gpst(t,&week); //计算穿刺点地方时(E.5.10)
tt-=floor(tt/86400.0)*86400.0; /* 0<=tt<86400 */
/* slant factor */
f=1.0+16.0*pow(0.53-azel[1]/PI,3.0); //计算投影系数(E.5.11)
/* ionospheric delay */
amp=ion[0]+phi*(ion[1]+phi*(ion[2]+phi*ion[3]));
per=ion[4]+phi*(ion[5]+phi*(ion[6]+phi*ion[7]));
amp=amp< 0.0? 0.0:amp;
per=per<72000.0?72000.0:per;
x=2.0*PI*(tt-50400.0)/per; //(E.5.12)
return CLIGHT*f*(fabs(x)<1.57?5E-9+amp*(1.0+x*x*(-0.5+x*x/24.0)):5E-9); //(E.5.13)
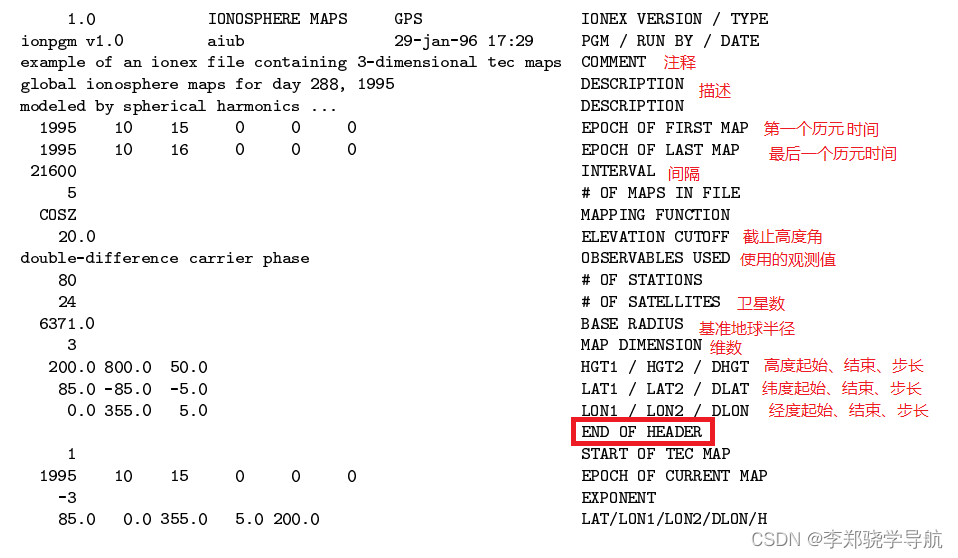
}分四大部分:文件头结束于END OF HEADER。多组总电子含量,每组以START OF TEC MAP ,结束于END OF TEC MAP 。多组电子含量均方根误差 ,与总电子含量对应,开始于START OF RMS MAP,结束于END OF RMS MAP,DCB数据块开始于START OF AUS DATA,结束于END OF AUS DATA,也称辅助数据块(Auxiliary Data Blocks)。
typedef struct { /* TEC grid type */
gtime_t time; /* epoch time (GPST) */
int ndata[3]; /* TEC grid data size {nlat,nlon,nhgt} */
double rb; /* earth radius (km) */
double lats[3]; /* latitude start/interval (deg) */
double lons[3]; /* longitude start/interval (deg) */
double hgts[3]; /* heights start/interval (km) */
double *data; /* TEC grid data (tecu) */
float *rms; /* RMS values (tecu) */
} tec_t;- 其存储在
nav_t结构体tec中 ,nt表示tec数量
- 执行流程:
- 开辟内存空间
- 扩展
file的*到efile[],遍历efile[]: fopen()以读的方式打开- 调用
readionexh()读ionex文件头 - 调用
readionexb()读ionex文件体 ,其中会调用addtec()将tec格网数据存到nav->tec[] - 读取完之后,调用
combtec()合并tec格网数据 - 存DCB参数到
nav->cbias
extern void readtec(const char *file, nav_t *nav, int opt)
{
FILE *fp;
double lats[3]={0},lons[3]={0},hgts[3]={0},rb=0.0,nexp=-1.0;
double dcb[MAXSAT]={0},rms[MAXSAT]={0};
int i,n;
char *efiles[MAXEXFILE];
trace(3,"readtec : file=%s\n",file);
/* clear of tec grid data option */
if (!opt) { //如果没有opt,释放nav->tec,nav->ntmax置0
free(nav->tec); nav->tec=NULL; nav->nt=nav->ntmax=0;
}
for (i=0;i<MAXEXFILE;i++) { //为efile[]开辟空间
if (!(efiles[i]=(char *)malloc(1024))) {
for (i--;i>=0;i--) free(efiles[i]);
return;
}
}
/* expand wild card in file path */
n=expath(file,efiles,MAXEXFILE); //扩展file的*到efile[]
//遍历efile[]
for (i=0;i<n;i++) {
if (!(fp=fopen(efiles[i],"r"))) { //以读的方式打开
trace(2,"ionex file open error %s\n",efiles[i]);
continue;
}
/* read ionex header */ //调用readionexh()读ionex文件头
if (readionexh(fp,lats,lons,hgts,&rb,&nexp,dcb,rms)<=0.0) {
trace(2,"ionex file format error %s\n",efiles[i]);
continue;
}
/* read ionex body */ //调用readionexb()读ionex文件体
readionexb(fp,lats,lons,hgts,rb,nexp,nav);
fclose(fp);
}
for (i=0;i<MAXEXFILE;i++) free(efiles[i]);
/* combine tec grid data */
if (nav->nt>0) combtec(nav); //调用combtec()合并tec格网数据
/* P1-P2 dcb */
for (i=0;i<MAXSAT;i++) {
nav->cbias[i][0]=CLIGHT*dcb[i]*1E-9; /* ns->m */ //存DCB到nav->cbias
}
}- 调用函数:
- readionexh():读取文件头,循环读取每一行,根据注释读取前面内容,如果遇到
START OF AUX DATA,调用readionexdcb()读取DCB参数。 - readionexdcb():循环读取DCB参数和对应的均方根误差,直到
END OF AUS DATA - readionexb():循环读取TEC格网数据和均方根误差,
type为1是TEC格网,type为2是均分根误差,调用addtec()将tec格网数据存到nav->tec[] - combtec():合并
nav->tec[]中时间相同的项。
- readionexh():读取文件头,循环读取每一行,根据注释读取前面内容,如果遇到
格网改正模型电离层格网模型文件IONEX,通过内插获得穿刺点位置,并结合当天电离层格网数据求出穿刺点的垂直电子含量,获得电离层延迟误差 。
由所属时间段两端端点的TEC网格数据时间插值计算出电离层延时 (L1) (m)
- 检测高度角和接收机高度是否大于阈值
- 从
nav_t.tec中找出第一个tec[i].time>time信号接收时间 - 确保 time是在所给出的
nav_t.tec包含的时间段之中 ,通过确认所找到的时间段的右端点减去左端点,来确保时间间隔不为0 - 调用
iondelay()来计算所属时间段两端端点的电离层延时 - 由两端的延时,插值计算出观测时间点处的值
extern int iontec(gtime_t time, const nav_t *nav, const double *pos,
const double *azel, int opt, double *delay, double *var)
{
double dels[2],vars[2],a,tt;
int i,stat[2];
trace(3,"iontec : time=%s pos=%.1f %.1f azel=%.1f %.1f\n",time_str(time,0),
pos[0]*R2D,pos[1]*R2D,azel[0]*R2D,azel[1]*R2D);
if (azel[1]<MIN_EL||pos[2]<MIN_HGT) { //检测高度角和接收机高度是否大于阈值
*delay=0.0;
*var=VAR_NOTEC;
return 1;
}
for (i=0;i<nav->nt;i++) { //从 nav_t.tec中找出第一个tec[i].time>time信号接收时间
if (timediff(nav->tec[i].time,time)>0.0) break;
}
if (i==0||i>=nav->nt) { //确保 time是在所给出的nav_t.tec包含的时间段之中
trace(2,"%s: tec grid out of period\n",time_str(time,0));
return 0;
}
if ((tt=timediff(nav->tec[i].time,nav->tec[i-1].time))==0.0) { //通过确认所找到的时间段的右端点减去左端点,来确保时间间隔 != 0
trace(2,"tec grid time interval error\n");
return 0;
}
/* ionospheric delay by tec grid data */ //调用 iondelay来计算所属时间段两端端点的电离层延时
stat[0]=iondelay(time,nav->tec+i-1,pos,azel,opt,dels ,vars );
stat[1]=iondelay(time,nav->tec+i ,pos,azel,opt,dels+1,vars+1);
//由两端的延时,插值计算出观测时间点处的值
if (!stat[0]&&!stat[1]) { //两个端点都计算出错,输出错误信息,返回 0
trace(2,"%s: tec grid out of area pos=%6.2f %7.2f azel=%6.1f %5.1f\n",
time_str(time,0),pos[0]*R2D,pos[1]*R2D,azel[0]*R2D,azel[1]*R2D);
return 0;
}
if (stat[0]&&stat[1]) { /* linear interpolation by time */ //两个端点都有值,线性插值出观测时间点的值,返回 1
a=timediff(time,nav->tec[i-1].time)/tt;
*delay=dels[0]*(1.0-a)+dels[1]*a;
*var =vars[0]*(1.0-a)+vars[1]*a;
}
else if (stat[0]) { /* nearest-neighbour extrapolation by time */ //只有一个端点有值,将其结果作为观测时间处的值,返回 1
*delay=dels[0];
*var =vars[0];
}
else {
*delay=dels[1];
*var =vars[1];
}
trace(3,"iontec : delay=%5.2f std=%5.2f\n",*delay,sqrt(*var));
return 1;
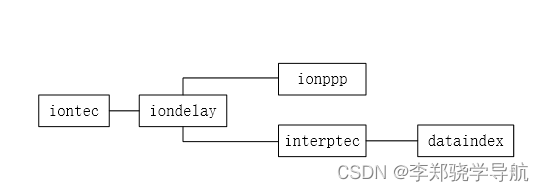
}- while大循环
tec->ndata[2]次: - 调用
ionppp()函数,计算当前电离层高度,穿刺点的位置 {lat,lon,h} (rad,m)和倾斜率 - 按照
M-SLM映射函数重新计算倾斜率 - 在日固系中考虑地球自转,重新计算穿刺点经度
- 调用
interptec()格网插值获取vtec *delay+=fact*fs*vtec,*var+=fact*fact*fs*fs*rms*rms
static int iondelay(gtime_t time, const tec_t *tec, const double *pos,
const double *azel, int opt, double *delay, double *var)
{
const double fact=40.30E16/FREQ1/FREQ1; /* tecu->L1 iono (m) */
double fs,posp[3]={0},vtec,rms,hion,rp;
int i;
trace(3,"iondelay: time=%s pos=%.1f %.1f azel=%.1f %.1f\n",time_str(time,0),
pos[0]*R2D,pos[1]*R2D,azel[0]*R2D,azel[1]*R2D);
*delay=*var=0.0;
//opt 模式选项 bit0: 0:earth-fixed,1:sun-fixed
// bit1: 0:single-layer,1:modified single-layer
for (i=0;i<tec->ndata[2];i++) { /* for a layer */
hion=tec->hgts[0]+tec->hgts[2]*i;
//调用ionppp()函数,计算当前电离层高度,穿刺点的位置 {lat,lon,h} (rad,m)和倾斜率
/* ionospheric pierce point position */
fs=ionppp(pos,azel,tec->rb,hion,posp);
if (opt&2) { //按照M-SLM映射函数重新计算倾斜率
/* modified single layer mapping function (M-SLM) ref [2] */
rp=tec->rb/(tec->rb+hion)*sin(0.9782*(PI/2.0-azel[1]));
fs=1.0/sqrt(1.0-rp*rp);
}
if (opt&1) { //在日固系中考虑地球自转,重新计算穿刺点经度
/* earth rotation correction (sun-fixed coordinate) */
posp[1]+=2.0*PI*timediff(time,tec->time)/86400.0;
}
/* interpolate tec grid data */ //格网插值获取vtec
if (!interptec(tec,i,posp,&vtec,&rms)) return 0;
*delay+=fact*fs*vtec;
*var+=fact*fact*fs*fs*rms*rms;
}
trace(4,"iondelay: delay=%7.2f std=%6.2f\n",*delay,sqrt(*var));
return 1;
}位置 {lat,lon,h} (rad,m)和倾斜率做返回值
extern double ionppp(const double *pos, const double *azel, double re,
double hion, double *posp)
{
double cosaz,rp,ap,sinap,tanap;
rp=re/(re+hion)*cos(azel[1]); //(E.5.15)
// z并不是仰角azel[1],而是仰角关于的补角,所以程序中在计算 rp是采用的是 cos(azel[1])的写法
ap=PI/2.0-azel[1]-asin(rp); //(E.5.14)(E.5.16)
sinap=sin(ap);
tanap=tan(ap);
cosaz=cos(azel[0]);
posp[0]=asin(sin(pos[0])*cos(ap)+cos(pos[0])*sinap*cosaz); //(E.5.17)
if ((pos[0]> 70.0*D2R&& tanap*cosaz>tan(PI/2.0-pos[0]))||
(pos[0]<-70.0*D2R&&-tanap*cosaz>tan(PI/2.0+pos[0]))) {
posp[1]=pos[1]+PI-asin(sinap*sin(azel[0])/cos(posp[0])); //(E.5.18a)
}
else {
posp[1]=pos[1]+asin(sinap*sin(azel[0])/cos(posp[0])); //(E.5.18b)
}
return 1.0/sqrt(1.0-rp*rp); //返回倾斜率
//可能因为后面再从 TEC网格数据中插值时,并不需要高度信息,所以这里穿刺点位置posp[2]没有赋值
}先判断点位是否在格网中,之后获取网格点的tec数据在 tec.data中的下标
static int dataindex(int i, int j, int k, const int *ndata) //(i:lat,j:lon,k:hgt)
{
if (i<0||ndata[0]<=i||j<0||ndata[1]<=j||k<0||ndata[2]<=k) return -1;
return i+ndata[0]*(j+ndata[1]*k);
}通过在经纬度网格点上进行双线性插值,计算第k个高度层时穿刺点处的电子数总量TEC
/* interpolate tec grid data -------------------------------------------- -----
* args:tec_t *tec I tec grid data
* int k I 高度方向上的序号,可以理解为电离层序号
* double *posp I pierce point position {lat,lon,h} (rad,m)
* double *value O 计算得到的刺穿点处的电子数总量(tecu)
* double *rms O 所计算的电子数总量的误差的标准差(tecu)
---------------------------------------------------------------------------- */
static int interptec(const tec_t *tec, int k, const double *posp, double *value,
double *rms)
{
double dlat,dlon,a,b,d[4]={0},r[4]={0};
int i,j,n,index;
trace(3,"interptec: k=%d posp=%.2f %.2f\n",k,posp[0]*R2D,posp[1]*R2D);
*value=*rms=0.0; //将 value和 rms所指向的值置为 0
if (tec->lats[2]==0.0||tec->lons[2]==0.0) return 0; //检验 tec的纬度和经度间隔是否为 0。是,则直接返回 0
//将穿刺点的经纬度分别减去网格点的起始经纬度,再除以网格点间距,对结果进行取整,
//得到穿刺点所在网格的序号和穿刺点所在网格的位置(比例) i,j
dlat=posp[0]*R2D-tec->lats[0];
dlon=posp[1]*R2D-tec->lons[0];
if (tec->lons[2]>0.0) dlon-=floor( dlon/360)*360.0; /* 0<=dlon<360 */
else dlon+=floor(-dlon/360)*360.0; /* -360<dlon<=0 */
a=dlat/tec->lats[2];
b=dlon/tec->lons[2];
i=(int)floor(a); a-=i;
j=(int)floor(b); b-=j;
//调用 dataindex函数分别计算这些网格点的 tec数据在 tec.data中的下标,
//按从左下到右上的顺序
//从而得到这些网格点处的 TEC值和相应误差的标准差
/* get gridded tec data */
for (n=0;n<4;n++) {
if ((index=dataindex(i+(n%2),j+(n<2?0:1),k,tec->ndata))<0) continue;
d[n]=tec->data[index];
r[n]=tec->rms [index];
}
if (d[0]>0.0&&d[1]>0.0&&d[2]>0.0&&d[3]>0.0) {
//穿刺点位于网格内,使用双线性插值计算出穿刺点的 TEC值
/* bilinear interpolation (inside of grid) */
*value=(1.0-a)*(1.0-b)*d[0]+a*(1.0-b)*d[1]+(1.0-a)*b*d[2]+a*b*d[3];
*rms =(1.0-a)*(1.0-b)*r[0]+a*(1.0-b)*r[1]+(1.0-a)*b*r[2]+a*b*r[3];
}
//穿刺点不位于网格内,使用最邻近的网格点值作为穿刺点的 TEC值,不过前提是网格点的 TEC>0
/* nearest-neighbour extrapolation (outside of grid) */
else if (a<=0.5&&b<=0.5&&d[0]>0.0) {*value=d[0]; *rms=r[0];}
else if (a> 0.5&&b<=0.5&&d[1]>0.0) {*value=d[1]; *rms=r[1];}
else if (a<=0.5&&b> 0.5&&d[2]>0.0) {*value=d[2]; *rms=r[2];}
else if (a> 0.5&&b> 0.5&&d[3]>0.0) {*value=d[3]; *rms=r[3];}
//否则,选用四个网格点中 >0的值的平均值作为穿刺点的 TEC值
else {
i=0;
for (n=0;n<4;n++) if (d[n]>0.0) {i++; *value+=d[n]; *rms+=r[n];}
if(i==0) return 0;
*value/=i; *rms/=i;
}
return 1;
}-
对流层延迟一般指非电离大气对电磁波的折射,折射效应大部分发生在对流层,因此称 为对流层延迟误差。对流层延迟影响与信号高度角有关,天顶方向影响能够达到2.3m,而高 度角较小时,其影响量可达 20m
-
对流层可视为非弥散介质,其折射率
$n$ 与电磁波频率$f$ 无关,于是 GPS 信号的群速率和相速率在对流层相等,无法使用类似消电离层的方法消除。 -
对流层延迟可以分为干延迟和湿延迟两部分,总的对流层延迟可以根据天顶方向干湿延 迟分量及其投影系数确定: $$ d_{trop}=d_{zpd}M_d(\theta)+d_{zpw}M_w(\theta) $$
在 rescode() 中被调用,调用 tropmodel()、sbstropcorr() 根据选项,计算对流层延迟 T
extern int tropcorr(gtime_t time, const nav_t *nav, const double *pos,
const double *azel, int tropopt, double *trp, double *var)
{
trace(4,"tropcorr: time=%s opt=%d pos=%.3f %.3f azel=%.3f %.3f\n",
time_str(time,3),tropopt,pos[0]*R2D,pos[1]*R2D,azel[0]*R2D,
azel[1]*R2D);
/* Saastamoinen model */
if (tropopt==TROPOPT_SAAS||tropopt==TROPOPT_EST||tropopt==TROPOPT_ESTG) {
*trp=tropmodel(time,pos,azel,REL_HUMI);
*var=SQR(ERR_SAAS/(sin(azel[1])+0.1));
return 1;
}
/* SBAS (MOPS) troposphere model */
if (tropopt==TROPOPT_SBAS) {
*trp=sbstropcorr(time,pos,azel,var);
return 1;
}
/* no correction */
*trp=0.0;
*var=tropopt==TROPOPT_OFF?SQR(ERR_TROP):0.0;
return 1;
}extern double tropmodel(gtime_t time, const double *pos, const double *azel,
double humi)
{
const double temp0=15.0; /* temparature at sea level */
double hgt,pres,temp,e,z,trph,trpw;
if (pos[2]<-100.0||1E4<pos[2]||azel[1]<=0) return 0.0;
/* standard atmosphere */
hgt=pos[2]<0.0?0.0:pos[2];
pres=1013.25*pow(1.0-2.2557E-5*hgt,5.2568); //求大气压P (E.5.1)
temp=temp0-6.5E-3*hgt+273.16; //求温度temp (E.5.2)
e=6.108*humi*exp((17.15*temp-4684.0)/(temp-38.45)); //求大气水汽压力e (E.5.3)
/* saastamoninen model */
z=PI/2.0-azel[1]; //求天顶角z 卫星高度角azel[1]的余角
trph=0.0022768*pres/(1.0-0.00266*cos(2.0*pos[0])-0.00028*hgt/1E3)/cos(z); //求静力学延迟Th
trpw=0.002277*(1255.0/temp+0.05)*e/cos(z); //求湿延迟Tw (E.5.4)
return trph+trpw; //Saastamoinen中对流层延迟为静力学延迟Th湿延迟Tw的和
}参考博客:RTKLIB中的卫星天线与接收机天线修正
-
天线相位中心,即天线]接收信号的电气中心,其空间位置在出厂时往往不在天线的几何中心上。天线所辐射出的电磁波在离开天线一定的距离后,其等相位面会近似为一个球面,该球面的球心即为该天线的等效相位中心,即天线相位中心(Antenna Phase Center )
-
GNSS观测量是相对于接收机天线的平均相位中心而言的,而接收机天线对中是相对于几何中也而言的,这两种中心一般不重合,两者之差就称为平均相位中心偏差(PCO),其大小可达毫米级或厘米级。且接收机天线的相位中也会随卫星信号输入的方向和强度的变化而变化,此时观测时刻的瞬时相位中也与平均相位中心的偏差称为平均相位中心变化(PCV),它与卫星的高度角和方位角有关。因此接收机天线相位偏差由接收机天线PCO和PCV两部分组成。
-
NGS提供的ANTEX格式天线模型,包含了卫星天线模型以及部分接收机天线模型。使用天线模型的目的包括:
- 修正天线参考点和天线相位中心的之间的偏差;
- 修正和仰角有关的误差;
- 修正L1和L2之间的相位中心偏差(这个误差可能对整周模糊度固定造成影响)
-
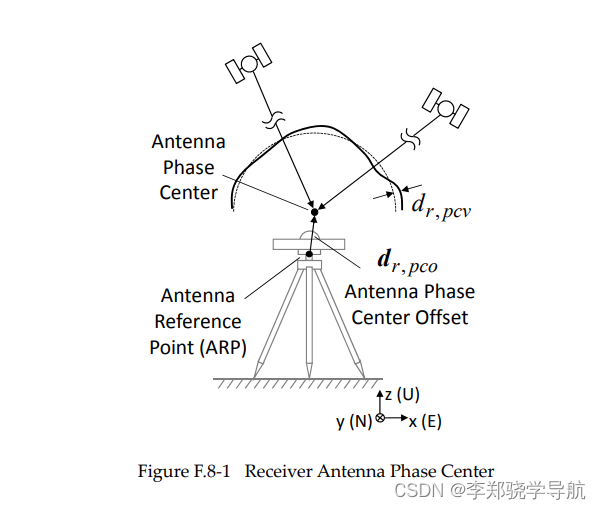
接收机天线相位中心模型:一般选取接收机天线底部与天线中轴的交点作为参考点(称天线参考点,ARP):
- ARP与实际相位中心的几何偏差值称为天线相位中心偏差(PCO)
- 由不同高度角、方位角测得的距离产生系统性的测量偏差为天线相位中心变化(PCV)
-
RTKLIB支持NGS PCV以及ANTEX格式的天线模型,其中包括了PCO和PCV修正参数。通过手册E.8章节可知,接收机天线修正如下:
-
PCO修正通常是当地坐标系ENU参数,因此需要利用转换矩阵转到ECEF坐标系
$$ \boldsymbol{d}{r, p c o, i}=\boldsymbol{E}{r}{ }^{T} \boldsymbol{d}_{r, p c o, i, e n u} $$ -
PCV修正则通过对高度角进行插值得到 $$ \boldsymbol{d}{r, p c o, i}=\boldsymbol{E}{r}{ }^{T} \boldsymbol{d}{r, p c o, i, e n u}d{r, p c v, i}(E l)=\frac{\left(E l-E l_{i}\right) d_{r, p c v, i}\left(E l_{i}\right)+\left(E l_{i+1}-E l\right) d_{r, p c v, i}\left(E l_{i+1}\right)}{E l_{i+1}-E l_{i}} $$
-
-
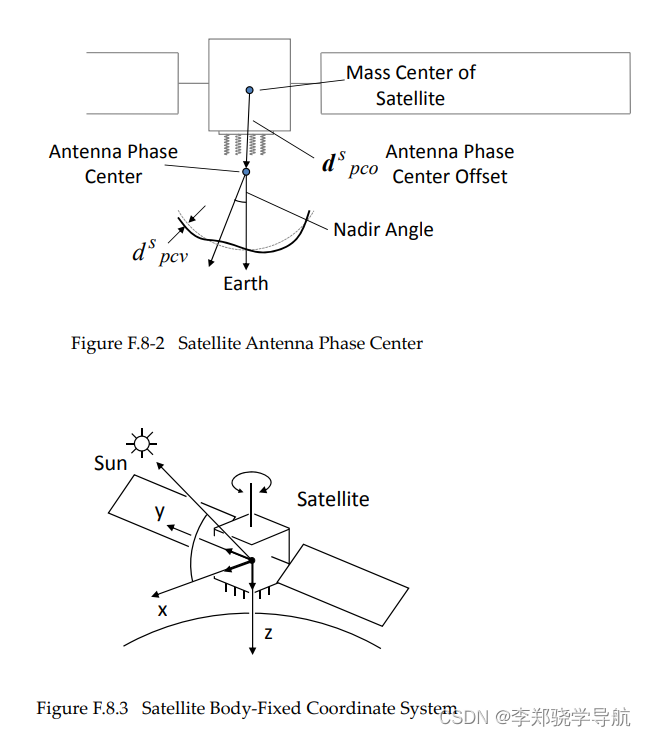
卫星天线相位中心模型:
卫星天线偏移(Satellite Antenna Offsets)是指卫星的天线相位中心与卫星质心的偏移。在PPP中我们需要用到精密星历。IGS 提供的精密星历(卫星位置)是相对卫星质心的,而载波相位、伪距测量值是相对天线相位中心的,因此我们需要计算PCV和PCO值,将所有值统一转换成相对天线相位中心。
readantex()函数有bug,接收机端同时出现GPS、GLO的PCO、PCV时,会用GLO系统的值覆盖GPS
`zdres()`函数:位于rtkpos.c中,调用`antmodel()`函数计算接收机端修正值,在`zdres_sat()`函数中进行修正。相对定位进行单差时,已经将卫星端的天线误差消除了,在处理相对定位中,可采用同一类型的天线且天线指北的方法从而消除接收机天线相位中也偏差的影响,但是在基线两端使用不用的天线时必须对其进行改正。执行流程如下:
- 计算LOS视向量在ENU中的单位矢量
e - 频段不同,天线的相位中心偏移(PCO)不同,先计算出每个频段天线在东、北、天三个方向总的偏移,即相位中心偏移
pcv->off与del[j]之和。 - 计算相位中心偏移(PCO)在观测单位矢量
e上的投影dot(off,e,3) - 计算天线相位中心变化量(PCV):不同的高度角,相位中心变化不同,因此根据高度角对
pcv->var[i]进行插值计算。 - PCO和PCV两部分求和为
dant[]
del为相对天线参考点偏移值
azel为方位角和俯仰角,
pcv->off为 phase center offset(PCO)
pcv->var为 phase center variations (PCV)
extern void antmodel(const pcv_t *pcv, const double *del, const double *azel,
int opt, double *dant)
{
double e[3],off[3],cosel=cos(azel[1]);
int i,j;
trace(4,"antmodel: azel=%6.1f %4.1f opt=%d\n",azel[0]*R2D,azel[1]*R2D,opt);
//计算LOS视向量在ENU中的单位矢量e
e[0]=sin(azel[0])*cosel;
e[1]=cos(azel[0])*cosel;
e[2]=sin(azel[1]);
//频段不同,天线的相位中心偏移(PCO)不同。
//先计算出每个频段天线在东、北、天三个方向总的偏移,即相位中心偏移pcv->off[i][j]与del[j]之和
for (i=0;i<NFREQ;i++) {
for (j=0;j<3;j++) off[j]=pcv->off[i][j]+del[j]; //相位中心偏移(PCO),pcv->off[i][j]中的值来自于天线PCV文件
//相位中心偏移(PCO)在观测单位矢量e上的投影dot(off,e,3)
//计算天线相位中心变化量(PCV):不同的高度角,相位中心变化不同,因此根据高度角对pcv->var[i]进行插值计算。
//dant[]为上面两部分相加
dant[i]=-dot(off,e,3)+(opt?interpvar(90.0-azel[1]*R2D,pcv->var[i]):0.0);
}
trace(5,"antmodel: dant=%6.3f %6.3f\n",dant[0],dant[1]);
}