capabilities.md

About GG's Capabilities

The term "GeneralizedGenerated", named after the generalization of Julia's generated functions, shows its design purpose and the real world problem it solved.

However, as the generated functions actually belongs to an advanced meta-programming part of Julia, for the sake of practical use, documentations and citations, we decide to write this document for giving some non-specialist and specialist introduction to GG.

A Use Case for Miraculous Speed-up

We present here a nice example to show how generated functions and GG enable high performance computations that cannot be made in traditional programming languages of both dynamic and static ones.

Suppose we have a matrix, and we want to sum its biggest circle inside.

To simply, we use an algorithm for an approximation of this result, where a preliminary implementation can be

function sum_circle(matrix::Array{F, 2}) where F
    (m, n) = size(matrix)
    (cx, cy) = center = ((m - 1) // 2, (n - 1) // 2)
    radius = min(cx, cy)
    s = zero(F)
    I = Int
    D = Float64
    xrange = I(cx-radius):I(cx+radius)
    yrange = I(cy-radius):I(cy+radius)
    radius = radius + 0.5
    for  x = xrange, y = yrange
        if hypot(D(cx - x), D(cy - y)) <= radius
            s += matrix[x + 1, y + 1]
        end
    end
    s
end

When benchmarking it,

using LinearAlgebra
using BenchmarkTools
data = rand(Int, (25, 25)) .% 500
julia> @btime sum_circle(data)
# Out:
   96.500 μs (1 allocation: 16 bytes)
-114514

The application of generated functions to this problem is due to the possibility of statically deciding the selection of points covered by the circle.

Say, if we already know the row number and col number of the given matrix, we can simply generate code for above computation:

I = Int
D = Float64
# `m n` are constants now
# the name of the array is `matrix`
(cx, cy) = center = ((m - 1) // 2, (n - 1) // 2)
radius = min(cx, cy)
s = zero(F)
xrange = I(cx-radius):I(cx+radius)
yrange = I(cy-radius):I(cy+radius)
radius = radius + 0.5
for  x = xrange, y = yrange
    if hypot(D(cx - x), D(cy - y)) <= radius
        s = :($s + $matrix[$(x + 1), $(y + 1)])
    end
end

By this way, we can got an AST in the form of 0 + arr[x1, y1] + arr[x2, y2] + arr[x3, y3] + ... + arr[xn, yn].

To make this possible, we need to type-encode the shape of matrix.

Thanks to Julia's type system, integers, and other data whose memory representations are sequential, can be used as types for dispatching(dynamic and static).

struct DimMatrix{M, N, F}
    data :: Array{F, 2}
end
matrix = ... # rand(Float32, (2, 3))
row, col = size(matrix)
DimMatrix{row, col, eltype(arr)}(matrix)

Now, I convince(IMPORTANT):

For any valid type F, given any runtime value arr :: Array{F, 2}, with a statically defined type DimMatrix, we can make one function as an amazingly fast version of sum_circle, which is capable of avoiding the computation of the selection for points in the circle implied by the matrix.

Firstly, we need to define a generator, which accepts a DimMatrix type, and the abstract syntax tree(matrix_ast) for representing the runtime value of the matrix, and return the computation logic.

From the perspective of Programming Languages, it's a type-directed code generation.

function sum_circle_generator(matrix_ast::Any, ::Type{DimMatrix{M, N, F}}) where {M, N, F}
    I = Int
    D = Float64
    (cx, cy) = center = ((M - 1) // 2, (N - 1) // 2)
    radius = min(cx, cy)
    s = zero(F)
    xrange = I(cx-radius):I(cx+radius)
    yrange = I(cy-radius):I(cy+radius)
    radius = radius + 0.5
    for  x = xrange, y = yrange
        if hypot(D(cx - x), D(cy - y)) <= radius
            s = :($s + $matrix_ast[$(x + 1), $(y + 1)])
        end
    end
    s
end

We can check it effects by some tiny data.

tiny_data = rand(Int, (4, 4)) .% 100
# Out:
    4×4 Array{Int64,2}:
    19   62  -95  -77
    20  -72  -59   42
    29  -70   85  -74
    -45   83  -54   40

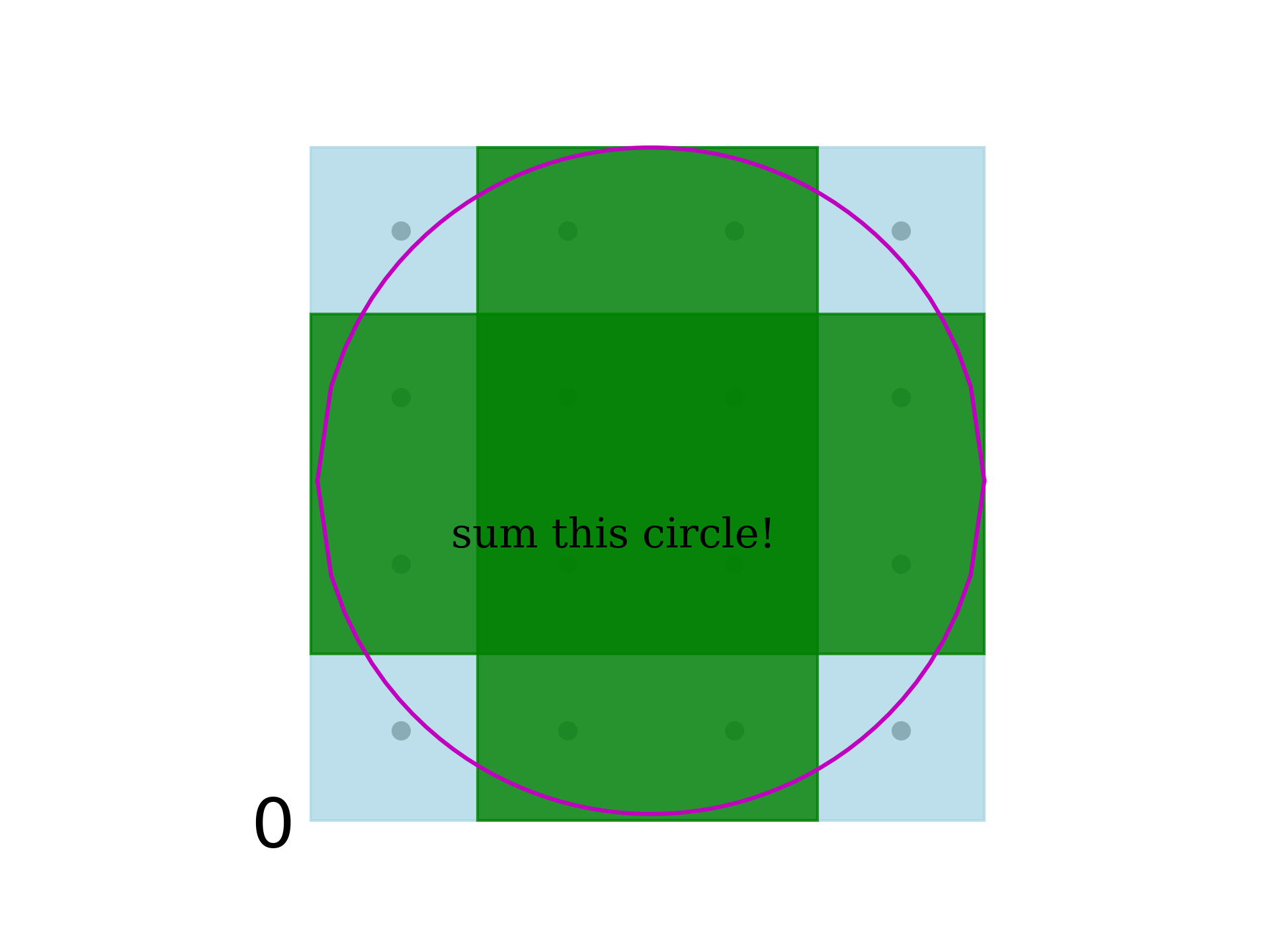
sum_circle_generator(:mat, DimMatrix{size(tiny_data)..., eltype(tiny_data)})
# Out:
    (((((((((((0 +
    mat[1, 2]) +
    mat[1, 3]) +
    mat[2, 1]) +
    mat[2, 2]) +
    mat[2, 3]) +
    mat[2, 4]) +
    mat[3, 1]) +
    mat[3, 2]) +
    mat[3, 3]) +
    mat[3, 4]) +
    mat[4, 2]) +
    mat[4, 3]

This is the plot of the selection of points.

Secondly, to execute above generated code in runtime without runtime overhead for any input matrix, we're supposed to use generated functions:

generated_sum_circle(mat::Array{F, 2}) where F =
    begin m, n = size(mat)
        generated_sum_circle(DimMatrix{m, n, F}(mat))
    end

@generated generated_sum_circle(mat::Ty) where{
        F, M, N, Ty <: DimMatrix{M, N, F}
    } = begin
        @assert mat == Ty # yes! that's it!
        sum_circle_generator(:(mat.data), Ty)
    end

In a generated function, we invoke the generator, and return the generated code. Its features are:

• Generating code once and only for each combination of argument types
• Working perfectly with JIT compilation and type inference
• If the type is inferred in compile time, the code generated in compile time; otherwise, type inference and generated code are made in runtime. Both ways are "zero-cost", if we don't take the overhead of JIT compilation into consideration.

From the perspective of Programming Languages, this mechanism shows an extension to staging techniques.

Now, we could try our generated function as an alternative to sum_circle, and enjoy a free lunch of more than 200x performance speed-up:

# In:
@btime generated_sum_circle(data)
# Out:
  413.065 ns (2 allocations: 32 bytes)
-114515


# polymorphic for other types:

# In:
data = rand(Float32, (25, 25));
@btime sum_circle(data)
# Out:
  96.500 μs (1 allocation: 16 bytes)
235.8246f0


# In:
@btime generated_sum_circle(data)
# Out:
  811.616 ns (2 allocations: 32 bytes)
235.8246f0

# In:
data = data = (rand(Int, (25, 25)) .% 100) .// 100;
@btime generated_sum_circle(data)

# Out:
  16.399 μs (2 allocations: 48 bytes)
-277//100

# In:
@btime sum_circle(data)
  123.099 μs (1 allocation: 32 bytes)
-277//100

I have good experience with more than 30 programming languages, and this is something we essentially cannot achieve in other programming languages, until now.

Restrictions

Generated functions are good, but its use didn't proliferate much, which is partially affected by the restrictions of generated functions.

The restrictions lie in 2 aspects, compiler overhead and expressiveness restriction due to implementation.

Compiler Overhead

One of the problem prevents the use of generated functions is, it burdens the compiler heavily. If number of used combinations of input parameters grows fast, you may feel there're some runtime delay caused by generated functions.

Triggering compilation and optimizations in runtime is a double-edged sword.

For instance, for the aforementioned example, the function generated_sum_circle cannot work for a really big matrix.

data = rand(Float32, (2500, 2500))
generated_sum_circle(data)
# Booom!

The direct reason for the crash of above code is, the generated code contains a π/4 2500 * 2500-depth addition expressions.

A simple fix is to manually reduce the size of generated code, by changing the generator sum_circle_generator:

function sum_circle_generator(matrix_ast::Any, ::Type{DimMatrix{M, N, F}}) where {M, N, F}
    I = Int
    D = Float64
    (cx, cy) = center = ((M - 1) // 2, (N - 1) // 2)
    radius = min(cx, cy)
    xrange = I(cx-radius):I(cx+radius)
    yrange = I(cy-radius):I(cy+radius)
    radius = radius + 0.5
    xs = Int[]
    ys = Int[]
    num_point = 0
    for  x = xrange, y = yrange
        if hypot(D(cx - x), D(cy - y)) <= radius
            push!(xs, x + 1)
            push!(ys, y + 1)
            num_point += 1
        end
    end
    quote s = 0
        xs :: Vector{Int} = $xs
        ys :: Vector{Int} = $ys
        for i in 1:$num_point
            x = xs[i] 
            y = ys[i]
            s += $matrix_ast[x, y]
        end
        s
    end
end

data = rand(Float32, (2500, 2500))
@btime generated_sum_circle(data)
  29.645 ms (4 allocations: 64 bytes)
2.4547852f6

@btime sum_circle(data)
  1.086 s (1 allocation: 16 bytes)
2.4547852f6

However, as it's not automatically made, it's not hard to imagine writing code in this way will be painful in some cases.

Expressiveness

Currently, the generated functions provided in Julia core is quite limited, and the most common case seen by users is, a generated function, its generator cannot return the code containing nested functions, i.e., we cannot generate functions by using generated functions.

@generated f(x) = :(() -> 1)
# f (generic function with 1 method)

f(1)
# ERROR: The function body AST defined by this @generated function
# is not pure.
# This likely means it contains a closure or comprehension.

What GeneralizedGenerated.jl did, is providing a mechanism to create functions from ASTs in runtime, and keeping away from performance loss when calling these runtime functions. Via this, we succeeded in ending the restrictions of returning closures in generated functions.

@gg f(x) = :(() -> 1 + x)
g = f(1)

The capability of generating functions is very important, and now, we're to introduce something that can only be made through creating functions in runtime with ASTs.

The Problems in Modeling

The good examples exist in working with modeling tasks, where we are always supposed to, create a domain specific language(DSL) to describe our models accurately.

However, in Julia, using any DSL example concerning to real world problems is too long. These DSLs usually take more than 50 lines, although concise, but still too verbose as an examplar. After failing at coming up with an example both making sense in practice and short enough,