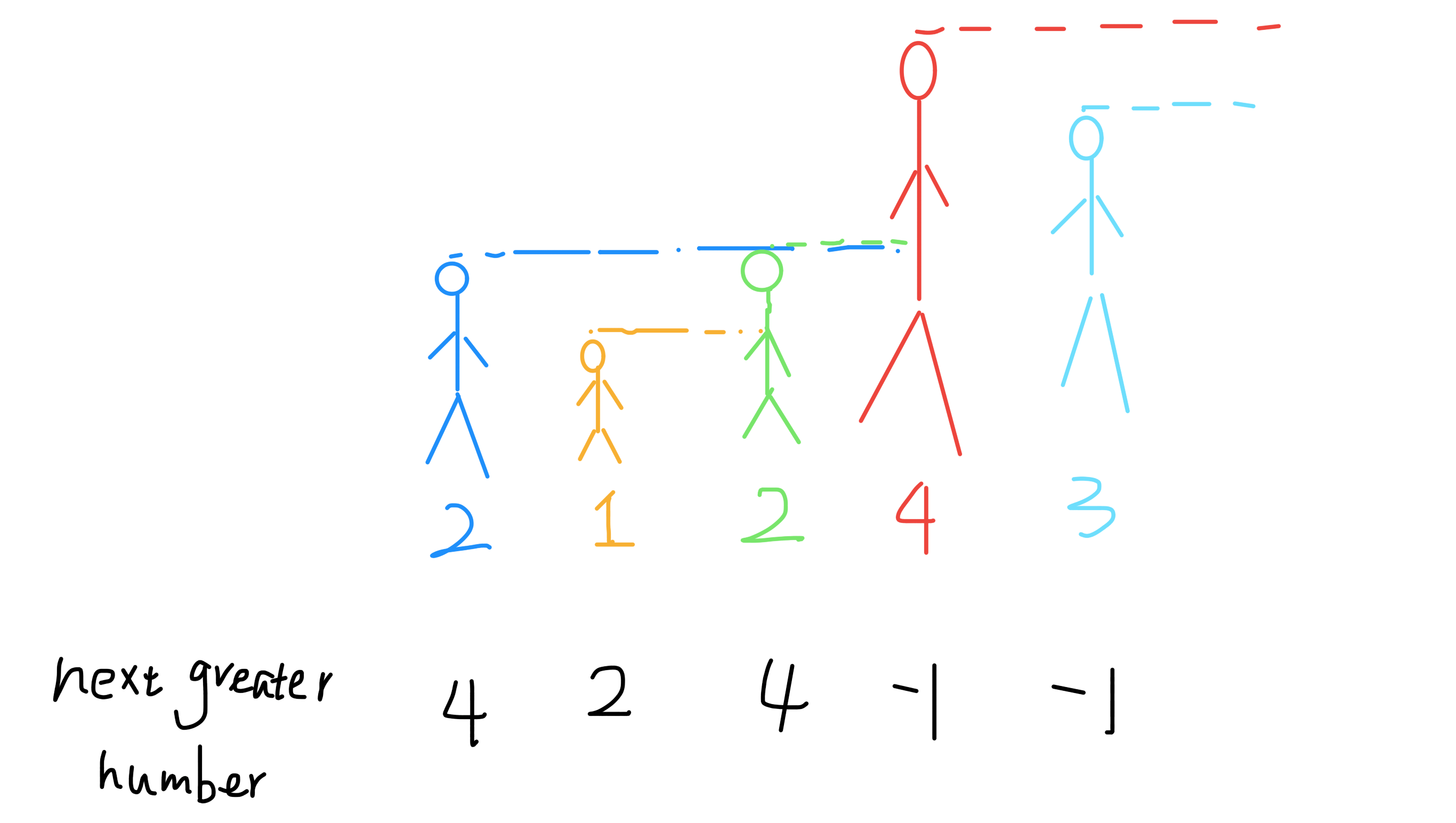顾名思义,单调栈就是单调的栈序列,有单调递减栈和单调递增栈两种
- 单调递减栈:从栈底到栈顶数据都是从大到小
- 单调递增栈:从栈底到栈顶数据都是从小到大
其实说法不是唯一,各有各的说法,有的说栈顶到栈底,这里我统一理解成:栈底到栈顶,想象一个栈水平放置,也就是从左往右看
单调栈主要用于在线性时间复杂度内解决 Next Greater Element 问题,对序列中每个元素找到下一个比它大的元素。
例如对于数组 [2,1,2,4,3],我们计算出 NGE 数组为 [4,2,4,-1,-1]
第一个元素 2 后面比 2 大的数是 4,第二个元素 1 后面比其大的数也是 4。以此类推,对于 4 而言后面没有比其大的数因此填 -1
其实可以将NGE 问题抽象成:数组的元素表示并列站着的人,元素大小表示人的身高,看下图:[第一个元素2] 第一个看到的人就是 [元素4],[元素1] 第一个看到的人就是 [第二个元素2]
再看代码:
//【推荐写法】从左往右看是非递增的
vector<int> NGE(vector<int>& h) {
int n = h.size();
vector<int> ans(n, -1); // 初始化为 -1 表示未处理的就是 -1
stack<int> st; // 保存下标
st.push(0); // 初始下标入栈
// 1. h[st.top()] > h[i] 直接入栈形成非递增
// 2. h[st.top()] == h[i] 直接入栈
// 3. h[st.top()] < h[i] 弹出时处理 ans
for (int i = 1; i < n; ++ i) {
if (h[st.top()] >= h[i]) { // 其实可以合并到下面
st.push(i);
} else {
while (!st.empty() && h[st.top()] < h[i]) {
int id = st.top();
st.pop();
ans[id] = h[i]; // h[id] 的 NGE 就是 h[i]
}
st.push(i);
}
}
return ans;
}
// 另一种倒着遍历的写法
vector<int> NGE(vector<int>& nums) {
int n = nums.size();
vector<int> ans(n);
stack<int> st;
// 倒着往栈里面放
for (int i = n - 1; i >= 0; -- i) {
while (!st.empty() && s.top() <= nums[i]) {
st.pop(); // 矮个起开,反正被挡住了,所以直接弹出
}
// 这个元素后面第一个高的个子
ans[i] = st.empty() ? -1 : st.top();
st.push(nums[i]);
}
return ans;
}按照上面的数据,最终栈剩余的数为 [4, 2]
给定一个数组 T = [73, 74, 75, 71, 69, 72, 76, 73],这个数组存放的是近几天的华氏温度,返回一个数组,对于每一天计算至少等多少天才能等到一个更加暖和的温度,如果等不到那一天就直接填 0
这个问题不是简单的求下一个更大的数,而是在找下一个更大的数距离此数的距离是多少,更直观的看下图。在上面只保存 Next Greater Element 的单调栈中需要另外保存 Next Greater Element Idx
所以代码如下:
//【推荐写法】从左往右看是非递增的
vector<int> NGE2(vector<int>& h) {
int n = h.size();
vector<int> ans(n, 0); // 初始化为 0 表示未处理的就是 0
stack<int> st; // 保存下标
st.push(0); // 初始下标入栈
// 1. h[st.top()] > h[i] 直接入栈形成非递增
// 2. h[st.top()] == h[i] 直接入栈
// 3. h[st.top()] < h[i] 弹出时处理 ans
for (int i = 1; i < n; ++ i) {
if (h[st.top()] >= h[i]) { // 其实可以合并到下面
st.push(i);
} else {
while (!st.empty() && h[st.top()] < h[i]) {
int id = st.top();
st.pop();
ans[id] = i - id; // NGE 的相隔天数
}
st.push(i);
}
}
return ans;
}
// 另一种倒着遍历的写法
vector<int> NGE2(vector<int>& nums) {
int n = nums.size();
vector<int> ans(n);
stack<pair<int,int>> st;
// 倒着往栈里面放
for (int i = n - 1; i >= 0; -- i) {
while (!st.empty() && st.top().first <= nums[i]) {
st.pop(); // 矮个起开,反正被挡住了,所以直接弹出
}
// 这里计算下一个更大元素的距离
ans[i] = st.empty() ? 0 : st.top().second - i;
st.push(pair<int, int>(nums[i], i));
}
return ans;
}考虑求环形数组的下一个更大的元素,例如给定数组 [2,1,2,4,3],返回数组 [4,2,4,-1,4]。由于拥有了环形属性,最后一个元素 3 绕了一圈后找到了比自己大的元素 4
为了得到 Next 更大的数,我们需要环形查找整个数组,也就是 Next 的概念不仅仅是当前元素的右边,而有可能是当前元素的左边
为此我们将原始数组“翻倍”,就是在后面再接一个原始数组,这样的话,按照之前“比身高”的流程,每个元素不仅可以比较自己右边的元素,而且也可以和左边的元素比较了。
代码如下:使用 % 运算循环获取元素
//【推荐写法】从左往右看是非递增的
vector<int> NGE(vector<int>& h) {
int n = h.size();
vector<int> ans(n, -1); // 初始化为 -1 表示未处理的就是 -1
stack<int> st; // 保存下标
st.push(0); // 初始下标入栈
// 1. h[st.top()] > h[i] 直接入栈形成非递增
// 2. h[st.top()] == h[i] 直接入栈
// 3. h[st.top()] < h[i] 弹出时处理 ans
for (int i = 1; i < 2*n; ++ i) {
if (h[st.top()] >= h[i%n]) { // 其实可以合并到下面
st.push(i%n);
} else {
while (!st.empty() && h[st.top()] < h[i%n]) {
int id = st.top();
st.pop();
ans[id] = h[i%n]; // h[id] 的 NGE 就是 h[i]
}
st.push(i%n);
}
}
return ans;
}
// 另一种倒着遍历的写法
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
vector<int> res(n); // 存放结果
stack<int> s;
// 假装这个数组长度翻倍了
for (int i = 2 * n - 1; i >= 0; i--) {
while (!s.empty() && s.top() <= nums[i % n])
s.pop();
res[i % n] = s.empty() ? -1 : s.top();
s.push(nums[i % n]);
}
return res;
}基础
| 题目 | 解析 | 答案 |
|---|---|---|
| 496. 下一个更大元素 I | 对nums2使用单调递减栈求NGE | 通过 |
| 503. 下一个更大元素 II | 原数组扩一倍,然后使用%运算 | 通过 |
| 739. 每日温度 | 保存 NGE 数和对应的下标 | 通过 |
| 1019. 链表中的下一个更大节点 | 和 496 一样,只是需要先遍历链表得到数组 | 通过 |
| 907. 子数组的最小值之和 | 求 a[i] 的左右边界,两次使用单调递增栈求边界 | 0x3F |
进阶
| 题目 | 解析 | 答案 |
|---|---|---|
| 42. 接雨水 | 栈底到栈顶是递减的,注意凹槽的位置 🔥 | 通过 |
| 84. 柱状图中最大的矩形 | 栈底到栈顶是递增的,注意凸起的位置 🔥 | 通过 |
| 901. 股票价格跨度 | 单调递减栈,先记下入栈之前数的下标 | 通过 |
| 402. 移掉 K 位数字 | 单调递增栈,从头开始遍历,最终去掉前导0 | 通过 |
| 1673. 找出最具竞争力的子序列 | 和 402 类似,不需要去掉前导0 | 通过 |
| 1081. 不同字符的最小子序列 | 和 316. 去除重复字母 一样,402 升级版,统计每个字符数目, | 通过 |
| 321. 拼接最大数 | 单调递减栈,数组字典序最大(cpp造轮子),归并 | 通过 |
| 1124. 表现良好的最长时间段 | 确切说不是单调栈,思想类似,前缀和+单调栈:找递减序列并且从后往前遍历,前缀和+哈希表:记录 s <= 0 的最小下标 |
0x3F |
正向遍历,移除元素或者保留元素使得剩下的数字最小(最大)或者剩下的序列字典序最小(最大)
单调队列
| 题目 | 解析 | 答案 |
|---|---|---|
| 239. 滑动窗口最大值 | 双端队列,很严格递减的,存储元素比较好理解 | 流程 |
| 862. 和至少为 K 的最短子数组 | 前缀和,单调递增的队列 | 0x3F |
| 2373. 矩阵中的局部最大值 | 3*3数据量比较小可以直接遍历,如果比较大可以每行执行滑动窗口求最大,并且每列比较 | 图解 |
总结
其实下面说的很繁琐?遇到题目就自己举几个例子模拟一下就知道了!下面不用记住
判断什么时候应该用单调递增的栈,什么时候应该用单调递减的栈
- 往前走找第一个比自己 「大」的元素,用单调递减的栈,也就是出栈的元素要求比自身要小,也就是
st.top() <= nums[i],所以最终栈里面剩余的元素是严格递减的 - 往前走找第一个比自己 「小」的元素,用单调递增的栈,也就是出栈的元素要求比自身要大,也就是
st.top() >= nums[i],所以最终栈里面剩余的元素是严格递增的
这里严格递增/减和非严格递增/减需要按照题目分析,一般而言都是 st.top() >= nums[i]或st.top() <= nums[i],也就是严格,但是也有例外,如 LC.84 的出栈条件就是 st.top() > price,也就是栈剩余元素都是非严格递增的(按照题意,得到的非严格递增栈所有元素都要出栈操作,最终栈为空~)